Jogos que não são de cassino - Perguntas frequentes
Eu gosto de jogar pôquer de mentirosos com notas de dólar. Qual é a probabilidade de sair qualquer combinação de 1, 2, 3, 4 ou 5 números iguais em uma nota? Obrigado. Se eu estiver jogando com 3 pessoas, qual é a probabilidade de sair qualquer número igual?
Primeiramente, permita-me responder à pergunta não formulada sobre a probabilidade de um número específico aparecer n vezes em uma nota aleatória. Uma nota possui 8 dígitos, portanto, a probabilidade de um número específico aparecer n vezes é dada por combin(8,n)* 0,1n *0,9 = 8-n / 10 = 8. A seguir, uma tabela mostrando a probabilidade de um número específico aparecer de 0 a 8.
Probabilidades de Números Específicos no Poker do Mentiroso
| Número | Probabilidade |
|---|---|
| 8 | 0,00000001 |
| 7 | 0,00000072 |
| 6 | 0,00002268 |
| 5 | 0,00040824 |
| 4 | 0,00459270 |
| 3 | 0,03306744 |
| 2 | 0,14880348 |
| 1 | 0,38263752 |
| 0 | 0,43046721 |
| Total | 1.00000000 |
A próxima tabela mostra a probabilidade de cada tipo possível de nota, categorizada pelo número de cada nota de um mesmo tipo (n-of-a-kind). Por exemplo, o número de série 66847680 teria uma nota de três notas do mesmo tipo, um par e três notas individuais, resultando em uma probabilidade de 0,1693440.
Probabilidades gerais no pôquer do mentiroso
| 8 carvalhos | 7 carvalhos | 6 carvalhos | 5 carvalhos | 4 carvalhos | 3 carvalhos | 2 carvalhos | 1 carvalho | Probabilidade |
|---|---|---|---|---|---|---|---|---|
| 1 | 0,0000001 | |||||||
| 1 | 1 | 0,0000072 | ||||||
| 1 | 1 | 0,0000252 | ||||||
| 1 | 2 | 0,0002016 | ||||||
| 1 | 1 | 0,0000504 | ||||||
| 1 | 1 | 1 | 0,0012096 | |||||
| 1 | 3 | 0,0028224 | ||||||
| 2 | 0,0000315 | |||||||
| 1 | 1 | 1 | 0,0020160 | |||||
| 1 | 2 | 0,0015120 | ||||||
| 1 | 1 | 2 | 0,0211680 | |||||
| 1 | 4 | 0,0211680 | ||||||
| 2 | 1 | 0,0020160 | ||||||
| 2 | 2 | 0,0141120 | ||||||
| 1 | 2 | 1 | 0,0423360 | |||||
| 1 | 1 | 3 | 0,1693440 | |||||
| 1 | 5 | 0,0846720 | ||||||
| 4 | 0,0052920 | |||||||
| 3 | 2 | 0,1270080 | ||||||
| 2 | 4 | 0,3175200 | ||||||
| 1 | 6 | 0,1693440 | ||||||
| 8 | 0,0181440 | |||||||
| Total | 1.0000000 | |||||||
carvalho = "de um tipo"
Para mais informações, consulte minha página sobre pôquer de mentirosos .
O Bank of America está oferecendo o triplo de um depósito selecionado por dia feito em um caixa eletrônico. A promoção dura cerca de dois meses. Minhas chances são melhores se eu depositar US$ 300... fazendo três depósitos de US$ 100 ou um de US$ 300... ou minhas chances gerais são tão baixas que a diferença não compensa o esforço?
Seu ganho esperado é o mesmo, independentemente de quantas vezes você divida o total dos seus depósitos. Uma boa estratégia seria depositar e sacar o mesmo valor repetidamente, o máximo de vezes possível. No entanto, suas chances podem ser tão baixas que não valha a pena o esforço.
Tenho uma dúvida sobre um jogo de dados oriental, onde os jogadores devem adivinhar qual lado do dado aparecerá. Os jogadores primeiro fazem suas apostas nos números 1, 2, 3, 4, 5 e 6 (como na roleta) e então o "dealer" lança 3 dados simultaneamente. Os pagamentos são de 1:1 se o número escolhido aparecer uma vez (em qualquer um dos 3 dados), 2:1 se o número escolhido aparecer duas vezes e 3:1 se o número escolhido aparecer em todos os 3 dados. Como o jogador pode fazer qualquer número de apostas no tabuleiro, qual seria o número ideal de apostas a serem feitas? (assumindo que todas as apostas sejam do mesmo valor)
A probabilidade de três acertos é 1/216. A probabilidade de dois acertos é 3*5/216. A probabilidade de um acerto é 25*5/216. A probabilidade de nenhum acerto é 5*5*5/216. Portanto, o retorno esperado é 3*(1/216)+2*(15/216)+1*(75/216)-1*(125/216)=-17/216=-7,87%. Não existe um número ideal de apostas; você perderá, independentemente da sua estratégia, 7,87% do valor total apostado.
Essas apostas podem ser feitas tanto no sic bo quanto no chuck a luck .
Quais são as chances de ganhar uma partida padrão de Klondike Solitaire, como na versão para Windows?
Essa é provavelmente a pergunta que mais me fazem e para a qual não tenho resposta. Nunca foi feito um jogo completo de Paciência Klondike. Talvez, quando os computadores forem milhões de vezes mais rápidos, alguém eventualmente o faça. No entanto, há rumores de que os cassinos de Las Vegas ofereciam o jogo pelo menos na década de 1950. Já pedi a vários veteranos de Las Vegas para confirmarem essa informação, mas nenhum deles conseguiu, até agora.
Recentemente, durante uma partida de gamão, tirei dois seis seguidos nos dados quatro vezes. Qual a probabilidade disso acontecer novamente?
A cada novo lançamento, a probabilidade de os próximos quatro lançamentos serem todos de dois seis é (1/36) 4 = 1 em 1679616.
Olá, no site www.transience.com.au/pearl.html tem um jogo chamado Pérolas para Porcos. As pérolas estão agrupadas em três fileiras (5+4+3) e, na sua vez, você pode remover quantas pérolas quiser de uma fileira. O objetivo do jogo é deixar a última pérola para o seu oponente pegar. O jogador (eu) sempre começa (e sempre perde). Por que eu nunca ganho? Meu oponente tem um sistema engenhoso para sempre vencer, você pode revelar o segredo dele?
Comece removendo 2 pérolas da fileira com 3, deixando 1+4+5. Independentemente do que seu oponente fizer na sua próxima jogada, deixe-o com uma das seguintes opções: 1+1+1, 1+2+3 ou 4+4. Com qualquer uma delas, force o oponente a uma situação com duas pilhas de 2 ou mais pérolas cada, ou um número ímpar de pilhas de 1 pérola cada.
Qual é o melhor conjunto de itens no Monopoly?
Eu prefiro o conjunto laranja. Ele oferece o melhor retorno sobre o investimento. Por exemplo, um hotel custa US$ 500 no conjunto laranja e o aluguel médio é de US$ 966,67, resultando em uma relação aluguel/despesa de 1,93. O único conjunto com uma relação maior é o azul claro, com 2,27. No entanto, o aluguel máximo no azul claro é de apenas US$ 600. Os aluguéis com três casas no conjunto laranja são os mesmos que os dos hotéis no azul claro, mas custam 20% menos, com espaço para construir mais. Além disso, o conjunto laranja é ideal para quem está saindo da prisão. Portanto, siga meu conselho e, ao negociar, tente conseguir o conjunto laranja.
Qual é o seu conselho para jogar pedra, papel e tesoura?
O melhor conselho deste site talvez seja este: na primeira rodada, SEMPRE ESCOLHA PAPEL. Isso porque jogadores amadores tendem a escolher pedra na primeira vez. Simplesmente estenda a mão em cada posição, uma de cada vez, e você verá que pedra é a escolha mais confortável e natural. Se você jogar rodadas repetidas, escolha o que venceria seu oponente na última rodada com probabilidade menor que um terço. Isso porque acredito que amadores repetem menos de um terço das vezes. Se estiver jogando contra um profissional que você teme que possa te desestabilizar, randomize olhando o ponteiro dos segundos do seu relógio, divida o número de segundos por três e pegue o resto. Em seguida, atribua o resto da seguinte forma: 0 = pedra, 1 = tesoura, 2 = papel (ou qualquer outra atribuição, desde que determinada com antecedência). Então, da próxima vez que for a um restaurante no estilo holandês, sugiro jogar uma única rodada para pagar a conta e depois escolher papel. Você me agradecerá depois.
Em Risk, quem leva vantagem quando o atacante rola três dados e o defensor rola dois?
Para quem não conhece o jogo, Risk é o melhor jogo de tabuleiro já criado. Quem nunca jogou não viveu de verdade. Respondendo à sua pergunta sobre uma partida comum de 3 contra 2, os resultados possíveis são os seguintes:
- O defensor perde em ambos os quesitos: 37,17%
- Cada um perde um: 33,58%
- O atacante perde em ambos os aspectos: 29,26%
No jogo Yahtzee, se restar apenas o próprio Yahtzee na cartela, qual é a probabilidade de formá-lo?
A tabela a seguir mostra a probabilidade de sucesso na última jogada, de acordo com o número de dados adicionais necessários para formar um Yahtzee.
Probabilidades do Yahtzee da Última Rodada
| Necessário | Probabilidade do Sucesso |
| 0 | 1 |
| 1 | 0,166667 |
| 2 | 0,027778 |
| 3 | 0,00463 |
| 4 | 0,000772 |
A próxima tabela mostra as probabilidades de melhoria. A coluna da esquerda mostra quantos dados você precisa antes de qualquer lançamento e a coluna superior mostra quantos você precisa depois do lançamento. O corpo da tabela mostra a probabilidade do grau de melhoria indicado.
Probabilidades de melhoria
| Precisa antes de rolar | 0 | 1 | 2 | 3 | 4 | Total |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0,166667 | 0,833333 | 0 | 0 | 0 | 1 |
| 2 | 0,027778 | 0,277778 | 0,694444 | 0 | 0 | 1 |
| 3 | 0,00463 | 0,069444 | 0,37037 | 0,555556 | 0 | 1 |
| 4 | 0,000772 | 0,01929 | 0,192901 | 0,694444 | 0,092593 | 1 |
A próxima tabela mostra a probabilidade, na jogada inicial, de precisar de 0 a 4 dados adicionais para formar um Yahtzee.
Probabilidades do primeiro lançamento de Yahtzee
| Necessário | Probabilidade |
| 0 | 0,000772 |
| 1 | 0,019290 |
| 2 | 0,192901 |
| 3 | 0,694444 |
| 4 | 0,092593 |
A próxima tabela mostra a probabilidade de melhoria e, consequentemente, de sucesso, de acordo com o número de dados necessários após a primeira jogada. Por exemplo, se o jogador precisar de mais 3 dados para fazer um Yahtzee, a probabilidade de precisar de apenas 2 dados após a segunda jogada e conseguir o Yahtzee na terceira jogada é de 0,010288066.
Probabilidades de Yahtzee após a primeira jogada, de acordo com o número necessário antes e depois da segunda jogada.
| Precisa antes de rolar | 0 | 1 | 2 | 3 | 4 | Total |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0,166667 | 0,138889 | 0 | 0 | 0 | 0,305556 |
| 2 | 0,027778 | 0,046296 | 0,01929 | 0 | 0 | 0,093364 |
| 3 | 0,00463 | 0,011574 | 0,010288 | 0,002572 | 0 | 0,029064 |
| 4 | 0,000772 | 0,003215 | 0,005358 | 0,003215 | 0,000071 | 0,012631 |
Para obter a resposta final, calcule o produto escalar do número necessário após a primeira rolagem, duas tabelas acima, e a probabilidade de sucesso final na coluna final, uma tabela acima. Isso resulta em 0,092593*0,012631 + 0,694444*0,029064 + 0,192901*0,093364 + 0,019290*0,305556 + 0,000772*1 = 4,6028643%. Para confirmar esse resultado, realizei uma simulação com 100.000.000 de jogos, e a probabilidade simulada foi de 4,60562%.
Se a dinamite for introduzida como uma opção no jogo pedra/papel/tesoura, onde a dinamite vence pedra e papel, mas a tesoura vence a dinamite, qual seria a estratégia ideal se dois lógicos perfeitos estivessem jogando?
Primeiro, podemos descartar completamente a possibilidade de jogar com papel. Independentemente do que a outra pessoa jogar, você se sairá melhor ou até mais rápido jogando dinamite do que com papel. Uma vez eliminado o papel, a dinamite essencialmente se torna o novo papel, vencendo pedra e perdendo para tesoura. Portanto, a estratégia perfeita é escolher aleatoriamente, e com igual probabilidade, entre pedra, tesoura e dinamite.
Qual a melhor estratégia em uma daquelas cabines onde o dinheiro voa para todos os lados enquanto você precisa coletar o máximo possível em um tempo limitado?
Fiz essa pergunta a Randy Hill, da Fun Industries Inc. Ele disse que você deve estender os braços, com as palmas das mãos voltadas para baixo, e deixar o dinheiro se acumular contra a parte inferior das mãos e dos braços. Quando tiver acumulado o suficiente, você o coloca na fenda.
Suponha que temos um jogo de azar. Uma moeda não viciada é lançada repetidamente. Para cada lançamento, temos que pagar 1 rupia. Existem dois resultados possíveis: cara (H) ou coroa (T). Se a diferença entre cara e coroa for 3, receberemos 8 rupias do apostador. Devemos jogar? Por quê? Qual é a nossa probabilidade de ganhar? Qual seria o impacto na probabilidade de ganhar se recebêssemos 7 ou 9 rupias?
Vamos chamar de x o número esperado de lançamentos a partir do ponto inicial.
Vamos chamar de y o número esperado de lançamentos restantes se um lado estiver com um lançamento a mais que o outro.
Vamos chamar de z o número esperado de lançamentos restantes se um dos lados estiver com dois lançamentos a mais que o outro.
E(x) = 1 + E(y)
E(y) = 1 + 0,5*E(x) + 0,5*E(z)
E(z) = 1 + 0,5*E(y)
É fácil perceber, por meio de álgebra matricial, que E(x) = 9, E(y) = 8 e E(z) = 5. Portanto, em média, serão necessárias 9 jogadas para que a diferença entre cara e coroa seja de 3. Assim, com uma aposta de 8 rúpias, é uma boa aposta para quem recebe uma rúpia por jogada, pois receberá em média 9 rúpias, mas terá um retorno de apenas 8. A vantagem da casa para o apostador é de 11,11%. Com 9 rúpias, é uma aposta justa; com 7 rúpias, a vantagem da casa é de 22,22%.
Em sua coluna de 28 de novembro de 2002, você abordou a estratégia adequada para o jogo Pearls Before Swine . Existe também uma sequência chamada Pearls Before Swine II . Como faço para vencer essa versão?
Na coluna de 28/11/2002, explico como jogar quando restam apenas três fileiras. Aqui está minha estratégia para quatro fileiras. Quando for sua vez, consulte a configuração na coluna da esquerda e jogue o que estiver na coluna da direita. Por exemplo, a posição inicial 3456 está listada por último e mostra que você deve remover 4 pérolas da fileira com 5, restando 1346. Se a coluna da esquerda indicar "Perder", não há como vencer se o oponente jogar a estratégia ideal, o que o jogo no Transcience sempre parece fazer.
Um padrão nesta tabela parece ser o de forçar o oponente a uma situação em que a soma das pérolas nas fileiras menor e maior seja igual à soma das duas fileiras do meio. Isso incluiria deixar zero na fileira com o menor número de pérolas.
Estratégia Pearls Before Swine II
| Você tem | Deixar |
| 1111 | 111 |
| 1112 | 111 |
| 1113 | 111 |
| 1114 | 111 |
| 1115 | 111 |
| 1116 | 111 |
| 1122 | Perder |
| 1123 | 1122 |
| 1124 | 1122 |
| 1125 | 1122 |
| 1126 | 1122 |
| 1133 | Perder |
| 1134 | 1133 |
| 1135 | 1133 |
| 1136 | 1133 |
| 1144 | Perder |
| 1145 | 1144 |
| 1146 | 1144 |
| 1155 | Perder |
| 1156 | 1155 |
| 1222 | 1122 |
| 1223 | 1122 |
| 1224 | 1122 |
| 1225 | 1122 |
| 1226 | 1122 |
| 1233 | 123 |
| 1234 | 123 |
| 1235 | 123 |
| 1236 | 123 |
| 1244 | 1144 |
| 1245 | 145 |
| 1246 | 246 |
| 1255 | 1155 |
| 1256 | Perder |
| 1333 | 1133 |
| 1334 | 1133 |
| 1335 | 1133 |
| 1336 | 1133 |
| 1344 | 1144 |
| 1345 | 145 |
| 1346 | Perder |
| 1355 | 1155 |
| 1356 | 1256 |
| 1444 | 1144 |
| 1445 | 1144 |
| 1446 | 1144 |
| 1455 | 1155 |
| 1456 | 1346 |
| 2222 | Perder |
| 2223 | 2222 |
| 2224 | 2222 |
| 2225 | 2222 |
| 2226 | 2222 |
| 2233 | Perder |
| 2234 | 2233 |
| 2235 | 2233 |
| 2236 | 2233 |
| 2244 | Perder |
| 2245 | 2244 |
| 2246 | 2244 |
| 2255 | Perder |
| 2256 | 2255 |
| 2333 | 2233 |
| 2334 | 2233 |
| 2335 | 2233 |
| 2336 | 2233 |
| 2344 | 2244 |
| 2345 | Perder |
| 2346 | 1346 |
| 2355 | 2255 |
| 2356 | 2345 |
| 2444 | 2244 |
| 2445 | 2244 |
| 2446 | 2244 |
| 2455 | 2255 |
| 2456 | 2345 |
| 3333 | Perder |
| 3334 | 3333 |
| 3335 | 3333 |
| 3335 | 3333 |
| 3336 | 3333 |
| 3344 | Perder |
| 3345 | 3344 |
| 3346 | 3344 |
| 3355 | Perder |
| 3356 | 3355 |
| 3444 | 3344 |
| 3445 | 3344 |
| 3446 | 3344 |
| 3455 | 3355 |
| 3456 | 1346 |
Brad S. escreveu para acrescentar uma estratégia geral para qualquer número de pérolas e linhas. Primeiro, você decompõe cada linha em seus componentes binários. Por exemplo, a posição inicial do jogo Transcience seria a seguinte.
- 3 = 2+1
- 4 = 4
- 5 = 4+1
- 6 = 4 + 2
Em seguida, você tenta deixar um número par de cada potência de 2. Por exemplo, no exemplo acima, há dois 1, dois 2 e três 4. Portanto, há um 4 extra. Depois, você remove 4 de qualquer uma das linhas que contenham um termo 4. Continue fazendo isso até que seu oponente fique com 2, 2 ou um número ímpar de 1.
Experimente esta estratégia no jogo Pearl 3 , você ganhará sempre. Se você começar com um cenário perdedor, como eu fiz no jogo 10 (4+7+8+11), você pode clicar em "ir" para que ele jogue primeiro.
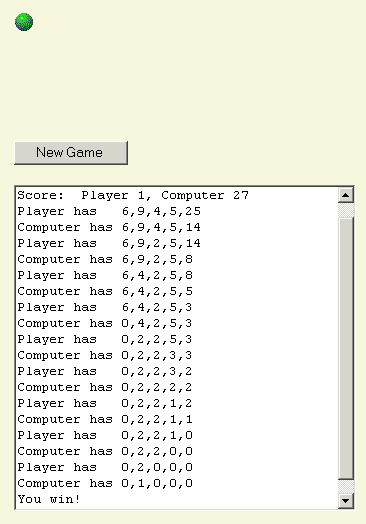
Eu não entendo seu jogo NIM ! Sempre achei que a chave para ganhar é deixar o oponente (nesse caso, o computador) com pontos cuja soma seja igual ao menor número binário correspondente, ou seja, se eu tiver 17 pontos, retiro 2 e deixo 15, que é a soma dos números binários 1, 2, 4 e 8. Mas isso não parece funcionar. Estou certo ou errado?
Você está no caminho certo com os números binários, mas essa não é exatamente a estratégia vencedora. Primeiro, se você puder deixar seu oponente com um número ímpar de linhas com apenas um elemento cada, faça isso. Caso contrário, decomponha cada linha em seus componentes binários. Por exemplo, 99 seria 64 + 32 + 2 + 1. Em seguida, some o número de cada componente em todas as linhas. Depois, procure uma jogada que deixe seu oponente com um número par de todos os componentes binários em todas as linhas.
Vejamos um exemplo. Suponha que seja a sua vez, com o seguinte cenário.
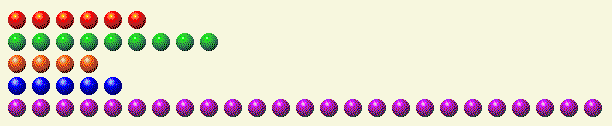
A tabela a seguir detalha cada linha em seus componentes binários.
Turno do Jogador 1
| Linha | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 25 | 1 | 0 | 0 | 1 | 1 |
| Total | 3 | 1 | 3 | 2 | 1 |
Você pode ver que há um número ímpar de uns, dois, quatros e dezesseis. Claramente, precisamos reduzir a linha de 25 para menos de 16 para eliminar a unidade 16. Para manter o total dos componentes binários par, precisamos remover o 1, adicionar um 2, adicionar um 4, manter o 8 e remover o 16. Isso significa que a melhor jogada é 2+4+8=14 na última linha. Deixando 14 na última linha, temos o seguinte.
Turno do computador 1
| Linha | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| Total | 2 | 2 | 4 | 2 | 0 |
O computador faz a sua parte, deixando-nos com isto.
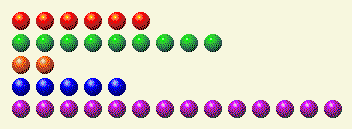
Aqui está a análise binária disso.
Turno do Jogador 2
| Linha | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| Total | 2 | 3 | 3 | 2 | 0 |
Aqui precisamos remover um 2 e um 4 para que os totais fiquem iguais. Há apenas uma linha, a 14, que contém ambos os componentes. Portanto, remova 6 dessa linha, restando 8.
Turno do Computador 2
| Linha | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| Total | 2 | 2 | 2 | 2 | 0 |
O computador faz a sua parte, deixando-nos com isto.
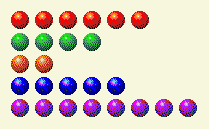
Agora precisamos alterar as colunas 1, 4 e 8.
Turno do Jogador 3
| Linha | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| Total | 1 | 2 | 3 | 1 | 0 |
Isso pode ser feito alterando a linha de 8 para 5, da seguinte forma.
Turno do Computador 3
| Linha | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| Total | 2 | 2 | 4 | 0 | 0 |
O computador faz a sua parte, deixando-nos com isto.
Agora precisamos alterar os totais de 2 e 4.
Turno do Jogador 4
| Linha | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Total | 2 | 3 | 3 | 0 | 0 |
Isso pode ser feito alterando o 6 para 0.
Turno 4 do computador
| Linha | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Total | 2 | 2 | 2 | 0 | 0 |
O computador faz a sua parte, deixando-nos com isto.
Agora precisamos trocar os números 2 e 4.
Turno do Jogador 5
| Linha | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Total | 2 | 3 | 1 | 0 | 0 |
Isso pode ser conseguido alterando a linha de 5 para 3. Se você conseguir levar seu oponente a uma situação x,x,y,y, você certamente vencerá, desde que consiga manter essa situação até o final.
Turno do Computador 5
| Linha | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Total | 2 | 4 | 0 | 0 | 0 |
Nas próximas jogadas, mantenho o computador nos padrões x,x,y,y. Aqui, o computador me deixa com 2,2,3,2; então, eu o deixo com 2,2,2,2.

O computador então me dá 2,2,1,2. Eu o deixo com 2,2,1,1.
O computador então me deixa com 2, 2, 1. Eu o deixo com 2, 2. Se você conseguir fazer com que seu oponente fique com duas fileiras iguais, você certamente ganhará; basta manter as fileiras iguais.

O computador então me deixa com uma única pilha de 2, e eu removo 1.

Aqui termina o jogo.
Recentemente adquiri uma roda da fortuna que pertencia ao meu tio-avô. Ela tem cerca de cem anos e estou tentando desenvolver um jogo para ela. Os números são de 1 a 60 em ordem aleatória e alternam entre preto e vermelho, com uma estrela verde a cada quinze números. Você poderia me ajudar a definir os valores dos prêmios para cada giro?
Portanto, existem 30 números pretos, 30 vermelhos e 4 verdes. Isso tornaria a probabilidade de sair um preto 30/64, um vermelho 30/64 e um verde 4/64. Se a probabilidade de um evento é p, então a probabilidade justa é de (1-p)/p para 1. Assim, a probabilidade justa para qualquer vermelho seria (34/64)/(30/64) = 34 para 30 = 17 para 15. O mesmo vale para o preto. A probabilidade justa para o verde é (60/64)/(4/64) = 60 para 4 = 15 para 1. Para um número específico, a probabilidade justa é de (63/64)/(1/64) para 63 para 1.
Sugiro pagar 1 para 1 no vermelho e no preto, 14 para 1 no verde e 60 para 1 em qualquer número individual. Uma fórmula para a vantagem da casa é (ta)/(t+1), onde t é a probabilidade real e a é a probabilidade verdadeira. Nesse caso, a vantagem da casa na aposta em vermelho ou preto é (63-60)/(63+1) = 3/64 = 4,69%. Na aposta em verde, a vantagem da casa é (15-14)/(15+1) = 1/16 = 6,25%. Em números individuais, a vantagem da casa é (63-60)/(63+1) = 3/64 = 4,69%.
No estado de Nova York, existem terminais de videoloteria (VLTs) em pontos de apostas fora das pistas de corrida. Você ouve a expressão "a máquina está se aproximando do seu ponto de ajuste" quando uma máquina de videoloteria "fica quente" e distribui mãos vencedoras uma após a outra. Isso explicaria por que a mesma máquina paga em um dia e não te reconhece em outros. Além disso, a maioria dessas máquinas não permite que você perca uma mão vencedora. Se você a descartar, ela retornará uma mão equivalente ou melhor. O que você acha disso?
As máquinas de videoloteria (VLTs) são jogos de raspadinha sofisticados. Existe um conjunto predeterminado de resultados. Quando você joga, o jogo escolhe um resultado aleatoriamente desse conjunto e exibe o prêmio para o jogador na forma de uma máquina caça-níqueis ou jogo de videopôquer. Como o resultado é predeterminado, qualquer elemento de habilidade é imaginário. Por exemplo, se você receber um royal flush e descartá-lo, receberá outro na próxima rodada. Normalmente, digo que, em jogos de azar, o passado não importa, mas, neste caso, há um efeito de descarte. Se você jogar uma vez e perder, isso aumentará marginalmente as chances dos resultados restantes do jogo, até que o estoque de raspadinhas virtuais se esgote e, presumo, o tambor virtual seja reabastecido. Acredito que suas oscilações entre vitórias e derrotas sejam apenas sorte normal e que qualquer predestinação seja imaginária.
Um leitor acrescentou posteriormente o seguinte a este tópico.
Tenho um comentário sobre sua coluna "Pergunte ao Mágico" de 14 de fevereiro (nº 183). Não tem muita relação com a pergunta que você respondeu. É apenas algo que você talvez ache interessante.
Antes da aprovação da Proposição 1A, que permitiu a implementação completa dos jogos de Classe 3, tínhamos uma pequena instalação de máquinas de videoloteria (VLT) por alguns anos. Em nosso sistema, operado pela SDG (agora parte da Bally), o prêmio inicial era de 4 milhões de sorteios. Quando o prêmio era reduzido para 2 milhões, um novo prêmio de 4 milhões era adicionado, totalizando 6 milhões de sorteios. Quando o prêmio era reduzido novamente para 2 milhões, o processo se repetia.
Qual é o número esperado de lançamentos de dados necessários para conseguir um Yahtzee?
Supondo que o jogador sempre tenha o número mais representado, a média é 11,09. Aqui está uma tabela mostrando a distribuição do número de lançamentos de dados em uma simulação aleatória de 82,6 milhões de tentativas.
Experimento Yahtzee
| Rolls | ocorrências | Probabilidade |
| 1 | 63908 | 0,00077371 |
| 2 | 977954 | 0,0118396 |
| 3 | 2758635 | 0,0333975 |
| 4 | 4504806 | 0,0545376 |
| 5 | 5776444 | 0,0699327 |
| 6 | 6491538 | 0,0785901 |
| 7 | 6727992 | 0,0814527 |
| 8 | 6601612 | 0,0799227 |
| 9 | 6246388 | 0,0756221 |
| 10 | 5741778 | 0,0695131 |
| 11 | 5174553 | 0,0626459 |
| 12 | 4591986 | 0,0555931 |
| 13 | 4022755 | 0,0487016 |
| 14 | 3492745 | 0,042285 |
| 15 | 3008766 | 0,0364257 |
| 16 | 2577969 | 0,0312103 |
| 17 | 2193272 | 0,0265529 |
| 18 | 1864107 | 0,0225679 |
| 19 | 1575763 | 0,019077 |
| 20 | 1329971 | 0,0161013 |
| 21 | 1118788 | 0,0135446 |
| 22 | 940519 | 0,0113864 |
| 23 | 791107 | 0,00957757 |
| 24 | 661672 | 0,00801056 |
| 25 | 554937 | 0,00671837 |
| 26 | 463901 | 0,00561624 |
| 27 | 387339 | 0,00468933 |
| 28 | 324079 | 0,00392347 |
| 29 | 271321 | 0,00328476 |
| 30 | 225978 | 0,00273581 |
| 31 | 189012 | 0,00228828 |
| 32 | 157709 | 0,00190931 |
| 33 | 131845 | 0,00159619 |
| 34 | 109592 | 0,00132678 |
| 35 | 91327 | 0,00110565 |
| 36 | 76216 | 0,00092271 |
| 37 | 63433 | 0,00076795 |
| 38 | 52786 | 0,00063906 |
| 39 | 44122 | 0,00053417 |
| 40 | 36785 | 0,00044534 |
| 41 | 30834 | 0,00037329 |
| 42 | 25494 | 0,00030864 |
| 43 | 21170 | 0,0002563 |
| 44 | 17767 | 0,0002151 |
| 45 | 14657 | 0,00017745 |
| 46 | 12410 | 0,00015024 |
| 47 | 10299 | 0,00012469 |
| 48 | 8666 | 0,00010492 |
| 49 | 7355 | 0,00008904 |
| 50 | 5901 | 0,00007144 |
| 51 | 5017 | 0,00006074 |
| 52 | 4227 | 0,00005117 |
| 53 | 3452 | 0,00004179 |
| 54 | 2888 | 0,00003496 |
| 55 | 2470 | 0,0000299 |
| 56 | 2012 | 0,00002436 |
| 57 | 1626 | 0,00001969 |
| 58 | 1391 | 0,00001684 |
| 59 | 1135 | 0,00001374 |
| 60 | 924 | 0,00001119 |
| 61 | 840 | 0,00001017 |
| 62 | 694 | 0,0000084 |
| 63 | 534 | 0,00000646 |
| 64 | 498 | 0,00000603 |
| 65 | 372 | 0,0000045 |
| 66 | 316 | 0,00000383 |
| 67 | 286 | 0,00000346 |
| 68 | 224 | 0,00000271 |
| 69 | 197 | 0,00000238 |
| 70 | 160 | 0,00000194 |
| 71 | 125 | 0,00000151 |
| 72 | 86 | 0,00000104 |
| 73 | 79 | 0,00000096 |
| 74 | 94 | 0.00000114 |
| 75 | 70 | 0,00000085 |
| 76 | 64 | 0,00000077 |
| 77 | 38 | 0,00000046 |
| 78 | 42 | 0,00000051 |
| 79 | 27 | 0,00000033 |
| 80 | 33 | 0,0000004 |
| 81 | 16 | 0,00000019 |
| 82 | 18 | 0,00000022 |
| 83 | 19 | 0,00000023 |
| 84 | 14 | 0,00000017 |
| 85 | 6 | 0,00000007 |
| 86 | 4 | 0,00000005 |
| 87 | 9 | 0,00000011 |
| 88 | 4 | 0,00000005 |
| 89 | 5 | 0,00000006 |
| 90 | 5 | 0,00000006 |
| 91 | 1 | 0,00000001 |
| 92 | 6 | 0,00000007 |
| 93 | 1 | 0,00000001 |
| 94 | 3 | 0,00000004 |
| 95 | 1 | 0,00000001 |
| 96 | 1 | 0,00000001 |
| 97 | 2 | 0,00000002 |
| 102 | 1 | 0,00000001 |
| Total | 82600000 | 1 |
Você conhece algum site que tenha uma boa análise das probabilidades/estatísticas/dados do gamão? E há algum livro específico que você recomendaria sobre algum aspecto do jogo?
Gamão é um dos meus jogos de azar favoritos. Não costumo escrever sobre ele porque partidas jogador contra jogador são extremamente difíceis de analisar. Além disso, não consigo encontrar nenhuma novidade interessante para explorar no jogo. Portanto, deixarei as dicas para outros. Aqui estão os recursos que sugiro:
Gamão, de Paul Magriel: Se existisse uma Bíblia do gamão, seria este livro. Sou um orgulhoso proprietário de uma antiga edição de capa dura. Este livro seria um ótimo ponto de partida. Embora tenha sido escrito em 1976, os conselhos ainda são válidos.
501 Problemas Essenciais de Gamão, de Bill Robertie: Há anos tento terminar este livro e ainda estou apenas na metade. É desanimador errar metade dos problemas, o suficiente para me fazer pensar que sou tão ruim em gamão quanto em golfe. No entanto, a cada problema errado, há uma lição valiosa a ser aprendida. Para jogadores de nível intermediário a avançado, este livro é uma ferramenta de aprendizado valiosa e, ao mesmo tempo, inspiradora.
Software de gamão Snowie : Jogo cerca de 1000 partidas por ano contra este jogo. O Snowie não só simula uma partida quase perfeita, como também indica exatamente o custo dos seus erros, assim que você os comete. Há muitas outras funcionalidades que eu nunca explorei. Se há uma coisa que aprendi com o Snowie, é que o maior problema no meu jogo são os erros crassos de não enxergar jogadas perfeitamente óbvias. Assim como no xadrez, um movimento ruim pode anular 100 bons movimentos.
Site da Motif : Antes de comprar o Snowie, joguei inúmeras partidas contra a Motif. A estratégia usada pela Motif é muito sólida, na minha opinião. Não há nada como jogar contra um oponente mais forte para aprimorar o seu próprio jogo.
Na coluna de 11 de abril de 2004, há uma pergunta sobre a estratégia adequada no programa "The Price is Right Showcase Showdown" . Supondo que a estratégia ideal seja seguida, qual é a probabilidade de cada jogador vencer?
A tabela a seguir mostra a probabilidade de cada jogador ganhar, de acordo com a primeira rodada do primeiro jogador, onde o jogador 1 joga primeiro, seguido pelo jogador 2 e, por último, o jogador 3. A última linha mostra as probabilidades gerais de vitória, antes da primeira rodada.
Probabilidades no Confronto do Showcase do The Price is Right
| Giro 1 | Estratégia | Jogador 1 | Jogador 2 | Jogador 3 |
| 0,05 | rodar | 20,59% | 37,55% | 41,85% |
| 0,10 | rodar | 20,59% | 37,55% | 41,86% |
| 0,15 | rodar | 20,57% | 37,55% | 41,87% |
| 0,20 | rodar | 20,55% | 37,55% | 41,9% |
| 0,25 | rodar | 20,5% | 37,56% | 41,94% |
| 0,30 | rodar | 20,43% | 37,56% | 42,01% |
| 0,35 | rodar | 20,33% | 37,58% | 42,10% |
| 0,40 | rodar | 20,18% | 37,60% | 42,22% |
| 0,45 | rodar | 19,97% | 37,64% | 42,39% |
| 0,50 | rodar | 19,68% | 37,71% | 42,61% |
| 0,55 | rodar | 19,26% | 37,81% | 42,93% |
| 0,60 | rodar | 18,67% | 37,96% | 43,36% |
| 0,65 | rodar | 17,86% | 38,21% | 43,93% |
| 0,70 | ficar | 21,56% | 38,28% | 40,16% |
| 0,75 | ficar | 28,42% | 35,21% | 36,38% |
| 0,80 | ficar | 36,82% | 31,26% | 31,92% |
| 0,85 | ficar | 46,99% | 26,35% | 26,66% |
| 0,90 | ficar | 59,17% | 20,36% | 20,47% |
| 0,95 | ficar | 73,61% | 13,19% | 13,21% |
| 1,00 | ficar | 90,57% | 4,72% | 4,72% |
| Média | 30,82% | 32,96% | 36,22% |
Aqui está o número de combinações vencedoras dentre as 6 possíveis no jogo 6x20 .
Jogador 1: 118.331.250Jogador 2: 126.566.457
Jogador 3: 139.102.293
Qual é a estratégia correta para Acey Deucey em um jogo de pôquer caseiro? Jogamos da seguinte forma: se a terceira carta for igual a uma das duas primeiras, a aposta é considerada um empate (push).
Na forma como você joga, onde uma combinação na terceira carta resulta em empate, as probabilidades ficam a seu favor quando há pelo menos seis valores diferentes entre as duas primeiras cartas (uma diferença de seis cartas). No meu caso, em Orange County, uma combinação na terceira carta resultava em uma dupla derrota. Nessa regra, as probabilidades ficam equilibradas com uma diferença de oito cartas. Se uma combinação na terceira carta resultar em uma derrota simples (1x), então você precisa de uma diferença de sete cartas para que as probabilidades estejam a seu favor.
No jogo de pôquer de uma carta, o baralho tem três cartas: um ás, um dois e um três. O ás é a carta mais baixa e o três a mais alta. Cada um dos dois jogadores aposta $1 no pote. Em seguida, cada jogador recebe uma carta. A ordem das apostas é predeterminada, com o jogador 1 agindo primeiro. O jogador 1 pode apostar $1 ou passar. Se o jogador 1 apostar, o jogador 2 pode pagar ou desistir. Se o jogador 1 passar, o jogador 2 pode apostar $1 ou passar. Se o jogador 1 passar e o jogador 2 apostar, o jogador 1 pode pagar ou desistir. Se ambos os jogadores passarem ou ambos apostarem, a carta mais alta ganha o pote. Supondo que ambos os jogadores sejam lógicos perfeitos, qual é a estratégia ótima para cada jogador?
Espero que esteja feliz; passei o dia todo nisso. A resposta e a solução podem ser encontradas no meu outro site mathproblems.info , problema 203, ou no artigo acadêmico "Game Theory and Poker" de Jason Swanson.
Estou pesquisando opções de financiamento imobiliário. Uma empresa está oferecendo uma taxa de juros de 5,75%, mais um ponto, para um financiamento fixo de 30 anos. Outra está cobrando 5,875% sem ponto. Qual é a melhor oferta?
Para o benefício de outros leitores, um ponto é uma comissão cobrada pelo empréstimo. Por exemplo, em um empréstimo de US$ 250.000, um ponto seria de US$ 2.500. Vou presumir que o mutuário adicionaria o ponto ao saldo principal e nunca amortizaria o principal antecipadamente.
A tabela a seguir mostra a taxa de juros equivalente sem o ponto, de acordo com a taxa de juros com um ponto e o prazo.
Taxa de juros equivalente sem pontos
| Taxa de juros com um ponto | 10 anos | 15 anos | 20 anos | 30 anos | 40 anos |
| 4,00% | 4,212% | 4,147% | 4,115% | 4,083% | 4,067% |
| 4,25% | 4,463% | 4,398% | 4,366% | 4,334% | 4,318% |
| 4,50% | 4,714% | 4,649% | 4,617% | 4,585% | 4,570% |
| 4,75% | 4,965% | 4,900% | 4,868% | 4,836% | 4,821% |
| 5,00% | 5,216% | 5,151% | 5,119% | 5,088% | 5,073% |
| 5,25% | 5,467% | 5,402% | 5,370% | 5,339% | 5,324% |
| 5,50% | 5,718% | 5,654% | 5,621% | 5,590% | 5,576% |
| 5,75% | 5,969% | 5,905% | 5,873% | 5,842% | 5,827% |
| 6,00% | 6,220% | 6,156% | 6,124% | 6,093% | 6,079% |
| 6,25% | 6,471% | 6,407% | 6,375% | 6,344% | 6,330% |
| 6,50% | 6,723% | 6,658% | 6,626% | 6,596% | 6,582% |
| 6,75% | 6,974% | 6,909% | 6,878% | 6,847% | 6,834% |
| 7,00% | 7,225% | 7,160% | 7,129% | 7,099% | 7,085% |
| 7,25% | 7,476% | 7,412% | 7,380% | 7,350% | 7,337% |
| 7,50% | 7,727% | 7,663% | 7,631% | 7,602% | 7,589% |
| 7,75% | 7,978% | 7,914% | 7,883% | 7,853% | 7,841% |
| 8,00% | 8,229% | 8,165% | 8,134% | 8,105% | 8,093% |
| 8,25% | 8,480% | 8,416% | 8,385% | 8,357% | 8,344% |
| 8,50% | 8,731% | 8,668% | 8,637% | 8,608% | 8,596% |
| 8,75% | 8,982% | 8,919% | 8,888% | 8,860% | 8,848% |
| 9,00% | 9,233% | 9,170% | 9,140% | 9,112% | 9,100% |
| 9,25% | 9,485% | 9,421% | 9,391% | 9,363% | 9,352% |
| 9,50% | 9,736% | 9,673% | 9,642% | 9,615% | 9,604% |
| 9,75% | 9,987% | 9,924% | 9,894% | 9,867% | 9,856% |
| 10,00% | 10,238% | 10,175% | 10,145% | 10,119% | 10,108% |
Isso demonstra que uma taxa de juros de 5,75% com um ponto é equivalente a 5,842% sem pontos. Em outras palavras, o pagamento seria o mesmo em ambos os casos, considerando que o ponto cobrado seja adicionado ao saldo principal. Sua outra oferta era de 5,875% sem pontos, que é superior a 5,842%, portanto, eu optaria pelos 5,75% com o ponto.
PS: Para quem estiver curioso sobre como resolvi o problema do "i", usei a função de taxa do Excel.
Meu filho acabou de fazer dois holes-in-one em um intervalo de duas semanas. Que coincidência! Ele tem handicap 1. O primeiro buraco foi de 151 jardas e o segundo de 137 jardas, em dois campos diferentes.
Segundo o livro "Life: the Odds (and How to Improve Them)" de Gregory Baer, a probabilidade de um hole-in-one em um buraco par 3 no PGA Tour é de 1 em 2491. Acredito que essas distâncias se enquadram na categoria de par 3.
Um handicap de 1 é muito bom, então não vou dar muito desconto em comparação com os jogadores do PGA Tour. Digamos que a probabilidade do seu filho acertar um buraco par 3 seja de 1 em 3.000. Um campo de golfe típico tem cerca de quatro buracos par 3. Digamos que seu filho jogue todos os dias. Isso daria 28 buracos par 3 por semana. A probabilidade de fazer exatamente dois hole-in-ones seria combin (28,2)×(1/3000) 2 ×(2999/3000) 26 = 1 em 24.017.
Recentemente, participei de um sorteio com 7.033 prêmios e a probabilidade de ganhar é de 1 em 13. Comprei 5 bilhetes. Qual é a minha probabilidade real de ganhar algo? Além disso, há 40 prêmios principais. Qual é a minha probabilidade de ganhar um prêmio principal?
Para simplificar, vamos ignorar o fato de que, quanto mais bilhetes você compra, menor se torna o valor de cada bilhete, pois você está competindo consigo mesmo. Dito isso, a probabilidade de perder todos os cinco bilhetes é (12/13) 5 = 67,02%. Portanto, a probabilidade de ganhar pelo menos um prêmio é de 32,98%. Há um total de 7033 × 13 = 91.429 bilhetes no tambor antes de você comprar qualquer um. 91.429 - 40 = 91.389 não são prêmios grandes. A probabilidade de não ganhar nenhum prêmio grande com cinco bilhetes é (91.389/91.429) 5 = 99,78%. Portanto, a probabilidade de ganhar pelo menos um prêmio grande é de 0,22%, ou 1 em 458.
No jogo de copas, cada jogador recebe 13 cartas. O naipe com o maior número de cartas dentre as 13 é chamado de "naipe longo", que pode ter de 4 a 13 cartas. Qual é a probabilidade de cada um desses totais?
Probabilidades para o naipe longo em Copas
| Cartões | Combinações | Probabilidade |
| 4 | 222766089260 | 0,35080524800183 |
| 5 | 281562853572 | 0,44339660045899 |
| 6 | 105080049360 | 0,16547685914958 |
| 7 | 22394644272 | 0,03526640326564 |
| 8 | 2963997036 | 0,00466761219692 |
| 9 | 235237860 | 0,00037044541245 |
| 10 | 10455016 | 0,00001646424055 |
| 11 | 231192 | 0,00000036407412 |
| 12 | 2028 | 0,00000000319363 |
| 13 | 4 | 0,00000000000630 |
| Total | 635013559600 | 1 |
A Regra dos 72 afirma que você divide a taxa de retorno anual por 72, e isso lhe dará o número de anos necessários para dobrar seu dinheiro. Por exemplo, um investimento que paga 10% ao ano levará 72/10 = 7,2 anos para dobrar de valor. Minha pergunta, talvez um tanto casual, é: por que 72?
Primeiramente, a "regra dos 72" é uma aproximação do tempo necessário para dobrar seu dinheiro, não uma resposta exata. A tabela a seguir mostra os valores da "regra dos 72" e o número exato de anos para diversas taxas de juros anuais.
Regra dos 72 — Anos para Dobrar o Dinheiro
| Taxa de juro | Regra dos 72 | Exato | Diferença |
|---|---|---|---|
| 0,01 | 72,00 | 69,66 | 2,34 |
| 0,02 | 36,00 | 35,00 | 1,00 |
| 0,03 | 24,00 | 23:45 | 0,55 |
| 0,04 | 18h00 | 17,67 | 0,33 |
| 0,05 | 14h40 | 14.21 | 0,19 |
| 0,06 | 12h00 | 11,90 | 0,10 |
| 0,07 | 10.29 | 10.24 | 0,04 |
| 0,08 | 9,00 | 9.01 | -0,01 |
| 0,09 | 8,00 | 8.04 | -0,04 |
| 0,10 | 7.20 | 7,27 | -0,07 |
| 0,11 | 6,55 | 6,64 | -0,10 |
| 0,12 | 6,00 | 6.12 | -0,12 |
| 0,13 | 5,54 | 5,67 | -0,13 |
| 0,14 | 5.14 | 5.29 | -0,15 |
| 0,15 | 4,80 | 4,96 | -0,16 |
| 0,16 | 4,50 | 4,67 | -0,17 |
| 0,17 | 4.24 | 4.41 | -0,18 |
| 0,18 | 4,00 | 4.19 | -0,19 |
| 0,19 | 3,79 | 3,98 | -0,20 |
| 0,20 | 3,60 | 3,80 | -0,20 |
Por que 72? Não precisa ser exatamente 72. Esse é apenas o número que funciona bem para taxas de juros realistas que você provavelmente encontrará em um investimento. Ele funciona quase exatamente para uma taxa de juros de 7,8469%. Não há nada de especial em 72, como há em π ou e. Por que qualquer número funciona? Se a taxa de juros for i, então vamos calcular o número de anos (y) necessários para dobrar um investimento.
2 = (1+i) y
ln(2) = ln(1+i) y
ln(2)= y×ln(1+i)
y = ln(2)/ln(1+i)
Esta pode não ser a minha melhor resposta de sempre, mas tente seguir esta lógica: seja y=ln(x).
dy/dx=1/x.
1/x ≈ x para valores de x próximos de 1.
Assim, dy/dx ≈ 1 para valores de x próximos de 1.
Portanto, a inclinação de ln(x) será próxima de 1 para valores de x próximos de 1.
Portanto, a inclinação de ln(1+x) será próxima de 1 para valores de x próximos de 0.
A "regra de 72" diz que 0,72/i =~ 0,6931/ln(1+i).
Estabelecemos que i e ln(1+i) são semelhantes para valores de i próximos de 0.
Assim, 1/i e 1/ln(1+i) são semelhantes para valores de i próximos de 0.
Usar 72 em vez de 69,31 ajusta as diferenças entre i e ln(1+i) para valores de i em torno de 8%.
Espero que isso faça algum sentido. Meus conhecimentos de cálculo estão bem enferrujados; levei horas para explicar isso para mim mesmo.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Numa feira de rua recente, havia um jogo com um tabuleiro de números, copos rasos e um copo com bolinhas, que envolvia adição. Não perguntei o nome do jogo e procurei na internet por cerca de uma hora, mas não encontrei nada a respeito. Pensei que você talvez tivesse alguma informação sobre ele, as probabilidades, ou pelo menos o nome.
O nome que a indústria dá a esse jogo é Razzle Dazzle. Lembro-me de tê-lo visto no sul da Califórnia quando criança e, no ano passado, em San Felipe, no México. Geralmente, ele é adaptado para se parecer com um jogo de futebol. Na minha opinião, esse jogo é o pior dos golpes em parques de diversões. O estado de Nova York deveria ter vergonha de permiti-lo. Segundo algumas pesquisas, as regras variam de lugar para lugar, mas a essência do golpe é sempre a mesma.
Baseia-se na mesma ilusão da aposta de campo no craps. Para aqueles que não estão familiarizados com a aposta de campo, o jogador ganha se a soma do lançamento de dois dados for 2, 3, 4, 9, 10, 11 ou 12. Os números perdedores são 5, 6, 7 e 8. As vitórias pagam o mesmo valor apostado, exceto o 2, que paga 2 para 1, e o 12, que paga 3 para 1 (exceto nos cassinos Harrah's, onde o pagamento é de 2 para 1 apenas no 12). O jogador com dificuldades em matemática pode erroneamente concluir que é uma boa aposta porque existem 7 totais vencedores e apenas 4 perdedores. A razão pela qual as probabilidades favorecem a casa é que os números perdedores têm a maior probabilidade de serem lançados.
Aqui estão as regras específicas do Razzle Dazzle, conforme extraídas do artigo "Probabilidades de Ganhar um Determinado Jogo de Parque de Diversões" , de Donald A. Berry e Ronald R. Regal, publicado na edição de novembro de 1978 da revista The American Statistician.
- O objetivo do jogo é avançar 100 jardas pelo campo de futebol. O jogador receberá algum tipo de prêmio ao conseguir.
- O jogador começa a pagar uma taxa específica por partida, como por exemplo, 1 dólar.
- O jogador irá espalhar 8 bolinhas de gude em uma grade de 11 por 13. Cada bolinha cairá em um dos 143 buracos.
- Cada buraco possui uma pontuação de 1 a 6. A tabela a seguir mostra a frequência de cada pontuação.
Distribuição de Pontos Razzle Dazzle
Pontos Número
a bordoProbabilidade 1 11 0,076923 2 19 0,132867 3 39 0,272727 4 44 0,307692 5 19 0,132867 6 11 0,076923 Total 143 1.000000 - O total de pontos será somado. O funcionário do parque de diversões consultará a tabela de conversão para verificar quantos metros o jogador avança. A tabela de conversão é mostrada abaixo.
Gráfico de Conversão Razzle Dazzle
Pontos Quintais
Ganho8 100 9 100 10 50 11 30 12 50 13 50 14 20 15 15 16 10 17 5 18 a 38 0 39 5 40 5 41 15 42 20 43 50 44 50 45 30 46 50 47 100 48 100 - Se o jogador rolar um total de 29, a taxa para todas as rolagens subsequentes será dobrada, e o jogador receberá um prêmio extra se e quando chegar ao outro lado do campo de futebol.
A média de pontos por bolinha de gude é 3,52, e o desvio padrão é 1,31. Observe como 3 e 4 pontos têm a maior probabilidade. Isso mantém o desvio padrão baixo e a soma de muitas bolinhas de gude próxima do esperado. Em comparação, o desvio padrão do lançamento de um único dado é 1,71.
Em seguida, observe como há 20 totais vencedores e 21 totais perdedores na tabela de conversão de jardas. O tipo de apostador que aposta em jogos de parque de diversões pode concluir erroneamente que sua probabilidade de avançar é de 20/41 ou 48,8%. Não me surpreenderia se os operadores do parque de diversões afirmassem falsamente que essas eram as probabilidades de avançar. No entanto, assim como na aposta no campo, os resultados mais prováveis não rendem nenhum prêmio.
A próxima tabela mostra a probabilidade de cada número de pontos por turno, jardas ganhas e jardas esperadas ganhas. A célula inferior direita mostra que a média de jardas ganhas por turno é de 0,0196.
Jardas esperadas por turno
| Pontos | Probabilidade | Quintais Ganho | Esperado Quintais Ganho |
| 8 | 0,00000000005 | 100 | 0,00000000464 |
| 9 | 0,00000000176 | 100 | 0,00000017647 |
| 10 | 0,00000002586 | 50 | 0,00000129285 |
| 11 | 0,00000022643 | 30 | 0,00000679305 |
| 12 | 0,00000143397 | 50 | 0,00007169849 |
| 13 | 0,00000713000 | 50 | 0,00035650022 |
| 14 | 0,00002926510 | 20 | 0,00058530196 |
| 15 | 0,00010234709 | 15 | 0,00153520642 |
| 16 | 0,00031168305 | 10 | 0,00311683054 |
| 17 | 0,00083981462 | 5 | 0,00419907311 |
| 18 | 0,00202563214 | 0 | 0,00000000000 |
| 19 | 0,00441368617 | 0 | 0,00000000000 |
| 20 | 0,00874847408 | 0 | 0,00000000000 |
| 21 | 0,01586193216 | 0 | 0,00000000000 |
| 22 | 0,02642117465 | 0 | 0,00000000000 |
| 23 | 0,04056887936 | 0 | 0,00000000000 |
| 24 | 0,05757346716 | 0 | 0,00000000000 |
| 25 | 0,07566411880 | 0 | 0,00000000000 |
| 26 | 0,09221675088 | 0 | 0,00000000000 |
| 27 | 0,10431970222 | 0 | 0,00000000000 |
| 28 | 0,10958441738 | 0 | 0,00000000000 |
| 29 | 0,10689316272 | 0 | 0,00000000000 |
| 30 | 0,09677806051 | 0 | 0,00000000000 |
| 31 | 0,08125426057 | 0 | 0,00000000000 |
| 32 | 0,06317871335 | 0 | 0,00000000000 |
| 33 | 0,04540984887 | 0 | 0,00000000000 |
| 34 | 0,03009743061 | 0 | 0,00000000000 |
| 35 | 0,01833921711 | 0 | 0,00000000000 |
| 36 | 0,01023355162 | 0 | 0,00000000000 |
| 37 | 0,00520465303 | 0 | 0,00000000000 |
| 38 | 0,00239815734 | 0 | 0,00000000000 |
| 39 | 0,00099365741 | 5 | 0,00496828705 |
| 40 | 0,00036673565 | 5 | 0,00183367827 |
| 41 | 0,00011909673 | 15 | 0,00178645089 |
| 42 | 0,00003349036 | 20 | 0,00066980729 |
| 43 | 0,00000797528 | 50 | 0,00039876403 |
| 44 | 0,00000155945 | 50 | 0,00007797235 |
| 45 | 0,00000023832 | 30 | 0,00000714969 |
| 46 | 0,00000002632 | 50 | 0,00000131607 |
| 47 | 0,00000000176 | 100 | 0,00000017647 |
| 48 | 0.00000000005 | 100 | 0,00000000464 |
| Totais | 1,00000000000 | 0 | 0,01961648451 |
Aqui estão alguns resultados de uma simulação aleatória de 17,5 milhões de jogos.
Resultados da Simulação Razzle Dazzle
| Pergunta | Responder |
| Probabilidade de avanço por turno | 0,0028 |
| Jardas esperadas por turno | 0,0196 |
| Jardas esperadas por avanço | 6,9698 |
| Número esperado de turnos por partida | 5238,7950 |
| Média de duplas por jogo | 559,9874 |
| Prêmios médios por jogo | 560,9874 |
Eu gostaria de ter indicado a aposta total média por jogo, mas meu computador não consegue processar números tão grandes. Em média, o jogador dobrou sua aposta 560 vezes ao longo de 5.239 rodadas por jogo. Em um dos jogos da simulação, o jogador dobrou sua aposta 1.800 vezes. Mesmo com uma média de 560 dobradas, a aposta por rodada seria de US$ 3,77 × 10¹⁶⁸ , considerando uma aposta inicial de US$ 1. Isso é muitas ordens de magnitude maior que o número de átomos no universo conhecido ( fonte ).
Até o jogador mais ingênuo não jogará por muito tempo se estiver avançando apenas uma vez a cada 355 jogadas. O que os operadores de cassino farão é trapacear a favor do jogador no início. Eles podem perceber que o jogador está jogando de graça ou mentir na soma dos pontos, dando ao jogador totais vencedores para aumentar sua confiança. Nunca joguei, mas imagino que, quando o jogador se aproxima da zona vermelha (20 jardas ou menos de um touchdown), o operador começará a jogar limpo. O jogador pode se perguntar por que de repente não está progredindo, mas com o dinheiro já investido e estando tão perto da linha de gol, ele hesitará em desistir e entregar as jardas pelas quais já pagou.
Ligações
- Razzle Dazzle , trecho do livro On the Midway.
- Fraude no jogo de tabuleiro Razzle Dazzle Carny em fliperama .
- Probabilidades de Ganhar um Determinado Jogo de Parque de Diversões por Donald A. Berry e Ronald R. Regal
Num carnaval recente, havia um jogo no estilo jogo da velha. Por £1 a rodada, você arremessava três bolas incrivelmente saltitantes em direção a uma grande caixa de madeira com 9 compartimentos no fundo. Supondo que cada bola caísse em um quadrado diferente, qual seria a probabilidade de ganhar?
Existem oito maneiras de ganhar: três linhas, três colunas e duas diagonais. Existem combin (9,3)=84 maneiras de escolher 3 quadrados de 9. Portanto, a probabilidade de ganhar é 8/84 = 9,52%.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Qual é a sua dica para jogar Monopoly?
Eis a estratégia básica do meu mago para o Monopoly:
- Compre tudo. Jogadores experientes podem abrir exceções se a propriedade não ajudar a criar um monopólio, bloquear outro jogador ou tiver pouco valor como moeda de troca. Serviços públicos também podem ser recusados em situações de falta de dinheiro.
- Negocie da melhor forma possível. É aqui que a habilidade entra em jogo. Tente negociar para obter o melhor conjunto que puder. Aqui está a minha classificação geral: Laranja, Amarelo, Azul Claro, Azul Escuro, Roxo Claro, Vermelho, Verde, Roxo Escuro. Essa classificação pode variar dependendo das circunstâncias. Em um jogo com pouco dinheiro, priorize os conjuntos mais baratos para desenvolver, como os azuis claros. Em um jogo com muito dinheiro, opte por aqueles em que há maior potencial de investimento, como os amarelos ou azuis escuros.
- Assim que você conseguir um conjunto de casas, seja por meios naturais ou comerciais, expanda rapidamente. Tente chegar a três casas em cada propriedade o mais rápido possível. O retorno marginal por casa cai depois de três. Hipoteque a maioria das suas outras propriedades e gaste seu dinheiro. Você precisa manter um pouco de patrimônio para pequenas despesas. Não gastar seu dinheiro é como um soldado em batalha que não usa suas balas.
- Rejeite todas as regras da casa absurdas. Isso vale especialmente para o prêmio em dinheiro do Estacionamento Gratuito (eu detesto isso!). Se você for mais habilidoso que seus oponentes, é importante minimizar o fator aleatório do jogo.
Se um macaco estivesse brincando com o Cubo de Rubik, qual seria a probabilidade de ele estar no padrão resolvido em um dado momento?
As seis faces centrais do cubo são fixas. Girando as faces, tudo o que você pode fazer é reorganizar os vértices e as arestas. Se você desmontasse o cubo, haveria 8! = 40.320 maneiras de organizar os oito vértices, sem levar em consideração a orientação de cada peça. Da mesma forma, existem 12! = 479.001.600 maneiras de organizar as 12 arestas, também sem levar em consideração a orientação.
Existem 3 maneiras de orientar cada canto, totalizando 3⁸ = 6.561 orientações de canto. Da mesma forma, existem duas maneiras de orientar cada peça da aresta, totalizando 2¹² = 4.096 orientações de aresta.
Portanto, se pudéssemos desmontar o cubo e reorganizar os grupos de arestas e vértices, haveria 8! × 12! × 3 8 × 2 12 = 519.024.039.293.878.000.000 permutações possíveis. No entanto, nem todas essas permutações podem ser obtidas a partir da posição inicial pela rotação das faces.
Primeiro, é impossível girar apenas um canto e deixar todo o resto igual. Nenhuma combinação de giros conseguirá isso. Basicamente, toda ação tem uma reação. Se você quiser girar um canto, isso afetará as outras peças de alguma forma. Da mesma forma, é impossível inverter apenas uma peça da borda. Por esses motivos, temos que dividir o número de permutações por 3 × 2 = 6.
Em segundo lugar, é impossível trocar duas peças de aresta sem perturbar o resto do cubo. Esta é a parte mais difícil de explicar desta resposta. Tudo o que você pode fazer com um Cubo de Rubik é girar uma face de cada vez. Cada movimento gira quatro peças de aresta e quatro peças de canto, totalizando oito peças movidas. Uma sequência de rotações pode ser representada por um número de movimentos de peças divisível por 8. Frequentemente, uma sequência de movimentos resultará em dois movimentos que se cancelam. No entanto, sempre haverá um número par de peças movidas em qualquer sequência de rotações. Trocar duas peças de aresta seria um movimento, um número ímpar, o que não pode ser alcançado com a soma de nenhum conjunto de números pares. Os matemáticos chamariam isso de problema de paridade. Portanto, temos que dividir por 2 novamente, porque duas peças de aresta não podem ser trocadas sem que outras peças sejam perturbadas.
Existem, portanto, 3 × 2 × 2 = 12 grupos possíveis de permutações do Cubo de Rubik. Se você desmontasse um Cubo de Rubik e o remontasse aleatoriamente, haveria uma chance de 1 em 12 de que ele fosse solucionável. Assim, o número total de permutações em um Cubo de Rubik é 8! × 12! × 3 = 12 × 2 = 12 / 12 = 43.252.003.274.489.900.000. Se você tivesse sete bilhões de macacos, aproximadamente a população mundial da humanidade, brincando aleatoriamente com o Cubo de Rubik, a uma taxa de uma rotação por segundo, um cubo passaria pela posição resolvida em média uma vez a cada 196 anos.
Ligações
Eu estava jogando Copas e recebi 10 cartas desse tipo. Qual a probabilidade disso acontecer?
Para quem não conhece as regras de Copas, o jogo começa com a distribuição de 13 cartas para cada um dos quatro jogadores. O naipe de copas é importante para o jogo, portanto, a quantidade de cartas de copas que você recebe é crucial. A tabela a seguir mostra as probabilidades de receber de 0 a 13 cartas de copas.
Probabilidade de 0 a 13 Copas em 13 cartas
| Corações | Combinações | Probabilidade | Inverso |
|---|---|---|---|
| 13 | 1 | 0,0000000000016 | 1 em 635.013.559.600,0 |
| 12 | 507 | 0,0000000007984 | 1 em 1.252.492.228,0 |
| 11 | 57.798 | 0,0000000910185 | 1 em 10.986.773,9 |
| 10 | 2.613.754 | 0,0000041160601 | 1 em 242.950,8 |
| 9 | 58.809.465 | 0,0000926113531 | 1 em 10.797,8 |
| 8 | 740.999.259 | 0,0011669030492 | 1 em 857,0 |
| 7 | 5.598.661.068 | 0,0088166008164 | 1 em 113,4 |
| 6 | 26.393.687.892 | 0,0415639752774 | 1 em 24,1 |
| 5 | 79.181.063.676 | 0,1246919258321 | 1 em 8,0 |
| 4 | 151.519.319.380 | 0,2386080062219 | 1 em 4,2 |
| 3 | 181.823.183.256 | 0,2863296074662 | 1 em 3,5 |
| 2 | 130.732.371.432 | 0,2058733541286 | 1 em 4,9 |
| 1 | 50.840.366.668 | 0,0800618599389 | 1 em 12,5 |
| 0 | 8.122.425.444 | 0,0127909480376 | 1 em 78,2 |
| Total | 635.013.559.600 | 1,0000000000000 |
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Para promoções de cassino que ainda usam bilhetes físicos em um tambor de verdade (não os eletrônicos), onde você imprime seus bilhetes no balcão de atendimento e os coloca no tambor, você dobra/amarra os bilhetes antes de colocá-los no tambor? Você acha que os bilhetes amassados têm mais chances de serem escolhidos?
Espero que você esteja feliz. Para responder a essa pergunta, comprei um rolo grande de bilhetes na Office Depot. Depois, coloquei 500 deles em um saco de papel, metade dobrado ao meio, em um ângulo de aproximadamente 90 graus, e a outra metade desdobrada. Em seguida, pedi a seis voluntários que sorteassem de 40 a 60 bilhetes cada, com reposição, enquanto eu anotava os resultados. Aqui estão os resultados.
Experimento de sorteio de bilhetes
| Assunto | Dobrado | Desdobrado | Total |
|---|---|---|---|
| 1 | 25 | 25 | 50 |
| 2 | 38 | 22 | 60 |
| 3 | 25 | 15 | 40 |
| 4 | 34 | 16 | 50 |
| 5 | 27 | 23 | 50 |
| 6 | 26 | 24 | 50 |
| Total | 175 | 125 | 300 |
Portanto, 58,3% dos bilhetes sorteados foram dobrados!
Se assumirmos que a desistência não teve efeito, então esses resultados estariam a 2,89 desvios padrão das expectativas. A probabilidade de obter essa quantidade de bilhetes desviados, ou mais, assumindo que a desistência não afetou as probabilidades, é de 0,19%, ou 1 em 514.
Eu acrescentaria que os participantes que sortearam os bilhetes às pressas tiveram muito mais probabilidade de tirar bilhetes dobrados. Já aqueles que dedicaram tempo a cada sorteio tiveram uma proporção de acerto próxima a 50/50.
Portanto, minha conclusão é definitivamente dobrá-las.
Para discutir este assunto, visite meu fórum no Wizard of Vegas .