Esportes - Perguntas frequentes
As probabilidades atuais para uma luta de boxe entre Vargas e Quartey são de -240 para Vargas e +190 para Quartey. Como isso funciona se eu apostar $100 em Vargas ou $100 em Quartey?
Uma aposta de $240 em Vargas renderá $100. Uma aposta de $100 em Quartey renderá $190. Claro, você pode apostar qualquer valor, mas os ganhos serão proporcionais. Se você apostar $100 em Vargas, ganhará $100 × (100/240) = $41,67.
Nas apostas esportivas contra o spread, parece-me que o vencedor paga a comissão de 10%, e não o perdedor. O que estou deixando passar?
Você pode encarar isso de duas maneiras. Por exemplo, suponha que você aposte 11 dólares para ganhar 10 dólares em um jogo.
Quem perde paga: Pode-se dizer que é uma aposta com chances iguais, com uma taxa reembolsável de US$ 1 caso você ganhe. Portanto, apenas quem perde acaba pagando a taxa.
O vencedor paga: Uma aposta justa com odds de 1 para 1 renderia US$ 11 para uma aposta de US$ 11. No entanto, se a aposta for vencedora, o ganhador recebe apenas US$ 10. O dólar faltante pode ser considerado uma comissão ou taxa.
Pessoalmente, considero que ambos os métodos de pagamento representam uma vantagem da casa de 4,54%, assumindo uma probabilidade de vitória de 50%.
Existem outros estados, além de Nevada, onde é legal apostar em esportes profissionais como beisebol e futebol americano?
O único estado além de Nevada com apostas esportivas legais é Delaware. Nesse estado, elas são administradas por meio de loteria, então as probabilidades são bem ruins.
Recentemente, estava olhando um bolão de futebol que estava rolando. Era um daqueles com uma grade de 100 quadrados, onde os números de 0 a 9 corriam nos eixos X e Y e correspondiam ao último gol do placar. Não sou fã de futebol e não apostei nesse bolão, mas como sou apostador, não acho que seja uma aposta muito boa.
Estou partindo do princípio de que você sabe a que tipo de bolão me refiro. Cada caixa custa US$ 5 e os prêmios são pagos a cada trimestre. Se a sua caixa for vencedora, você ganha US$ 125, e é possível ganhar nos 4 trimestres se os últimos números permanecerem os mesmos, ganhando US$ 500, o que representa um pagamento de 100 para 1.
A pessoa que me ofereceu a aposta estava tentando me convencer de que as chances de ganhar os 500 dólares são de 100 para 1. Discordo. Primeiro, a combinação com 0 + 7 tem uma chance muito maior de ganhar do que a combinação com 2 + 9. No entanto, a probabilidade de 0 + 7 permanecerem como os dois últimos números durante todo o jogo deve ser alta. Se as combinações forem escolhidas aleatoriamente, você poderia me dizer qual a probabilidade aproximada de ganhar o prêmio de 500 dólares?
Supondo que as células na grade sejam escolhidas aleatoriamente, a probabilidade de ganhar qualquer trimestre seria de 1/100. Supondo que cada trimestre fosse um evento independente, o que não é o caso, a probabilidade de ganhar todos os quatro trimestres seria de (1/100) ⁴ = 1 em 100 milhões.
Acabei de ler sua última seção "Pergunte ao Mago". Você disse que as apostas esportivas seriam uma das maneiras de ganhar a vida. Poderia explicar um pouco melhor? Elas oferecem uma vantagem semelhante sobre a casa de apostas, assim como o blackjack com contagem de cartas oferece sobre o cassino? Obrigado.
Infelizmente, não posso dar muitos detalhes. Apostas esportivas não são meu forte, embora eu pretenda aprender mais sobre o assunto quando tiver tempo. Posso dizer que é difícil comparar a lucratividade das apostas esportivas com a contagem de cartas. A contagem de cartas é muito técnica e segue regras à risca. Ganhar dinheiro com apostas esportivas exige mais discernimento e é mais sujeito a opiniões. Existem várias estratégias que podem ser usadas para ganhar dinheiro com apostas esportivas, por exemplo, buscar arbitragem apostando em ambos os lados em diferentes cassinos com diferentes spreads de pontos, explorar apostas de proposição incomuns ou apostar em acumuladas correlacionadas. Recomendo o livro "Sharp Sports Betting" de Stanford Wong para mais informações sobre como ganhar com apostas esportivas.
Já vi vários especialistas em apostas da NFL se gabando de suas porcentagens de acertos. Qual a probabilidade de um apostador aleatório acertar 50%, 55% e 60% dos palpites ao longo de 1, 3 e 5 temporadas?
A tabela a seguir mostra a probabilidade de atingir cada porcentagem de 50% a 60%, em incrementos de 1%, para cada número de temporadas de 1 a 5. Isso se baseia em uma temporada de 259 jogos. Também presumo que a porcentagem geral seja arredondada para baixo. Por exemplo, se um apostador acertasse 132 dos 259 jogos, para uma porcentagem de 50,97%, ele receberia crédito apenas por 50%, já que não atingiu 51%. Não me surpreenderia se esses apostadores exibicionistas estivessem arredondando os números a seu favor.
Probabilidade de apostas percentuais na NFL
| Razão | 1 Temporadas | 2 temporadas | 3 temporadas | 4 Estações | 5 estações |
| 0,5 | 0,5 | 0,517523 | 0,5 | 0,512393 | 0,5 |
| 0,51 | 0,354641 | 0,314437 | 0,282985 | 0,257059 | 0,234993 |
| 0,52 | 0,267178 | 0,178085 | 0,125486 | 0,101366 | 0,074229 |
| 0,53 | 0,160065 | 0,086589 | 0,049447 | 0,025155 | 0,015098 |
| 0,54 | 0,106982 | 0,035817 | 0,013066 | 0,004959 | 0,001926 |
| 0,55 | 0,053095 | 0,012519 | 0,002569 | 0,000687 | 0,000152 |
| 0,56 | 0,023385 | 0,00282 | 0,000373 | 0,000051 | 0,000007 |
| 0,57 | 0,012645 | 0,00067 | 0,000053 | 0,000003 | 0 |
| 0,58 | 0,00453 | 0,000133 | 0,000004 | 0 | 0 |
| 0,59 | 0,00213 | 0,000022 | 0 | 0 | 0 |
| 0,6 | 0,000617 | 0,000003 | 0 | 0 | 0 |
Gostaria da sua opinião sobre um bolão da NFL. Os bilhetes custam US$ 25 cada e consistem em três times aleatórios, em uma ordem específica. A cada semana, o ganhador com os três times com a maior pontuação, na ordem correta, ganha US$ 1.000. Qual é o valor real de cada bilhete?
A temporada regular da NFL tem 17 semanas e 32 times. A probabilidade de ganhar em qualquer semana é de 1 em 32 * 31 * 30 = 29760. O valor esperado de cada bilhete é de $1000 * 17 / 29760 = 57,12 centavos. Portanto, o retorno esperado é de 2,28%, ou uma vantagem da casa de 97,72%!
Desculpe incomodá-lo, como indica sua página na internet, mas você já utilizou seus conhecimentos de matemática para encontrar anomalias nas probabilidades de apostas esportivas ou calculou uma maneira de obter um retorno garantido com base nessas informações?
Nos últimos dois anos, tenho dedicado muito tempo às apostas esportivas, muito mais do que a qualquer outra forma de jogo. A menos que você possa apostar em duas casas de apostas diferentes, uma oportunidade muito rara, não há maneiras garantidas de ganhar dinheiro com apostas esportivas. É cedo demais para revelar segredos, mas procuro por qualquer aposta que pareça oferecer vantagem ao jogador e então faço minha aposta. Talvez você queira conferir algumas informações que publiquei recentemente no meu apêndice 2 sobre apostas esportivas .
Se o time de futebol americano de uma universidade tem 10% de chance de vencer o primeiro jogo, 30% de chance de vencer o segundo e 65% de chance de perder ambos os jogos, qual é a probabilidade de ele vencer exatamente uma vez?
Se assumíssemos que os jogos são independentes, a probabilidade de perder ambos seria de 90% * 70% = 63%. Mas, como você disse que a probabilidade de perder ambos é, na verdade, de 65% (que é maior que 63%), isso significa que os dois eventos estão correlacionados. Se a probabilidade de perder ambos é de 65% e a probabilidade de perder apenas o jogo 2 é de 70%, então a probabilidade de ganhar o jogo 1 e perder o jogo 2 deve ser de 5%. Usando a mesma lógica, a probabilidade de perder o jogo 1 e ganhar o jogo 2 deve ser de 25%. Isso deixa apenas 5% de probabilidade de ganhar ambos os jogos. Portanto, a probabilidade de ganhar exatamente uma vez é de 25% + 5% = 30%.
Minha pergunta era específica para o jogo de futebol americano de segunda-feira à noite (Dallas x Washington). Está chovendo em Washington há algumas horas. A chuva deve continuar durante o jogo e no dia seguinte. Gostaria de saber qual o efeito da chuva em uma aposta de mais/menos pontos na NFL? Existe alguma tendência ou outra dica que você possa me dar?
Não sei qual o efeito da chuva no total. No entanto, sei que os apostadores mais experientes levam o clima muito a sério e ajustam as linhas de acordo com a temperatura, a precipitação, a velocidade do vento e outros fatores semelhantes.
Olá, Wiz. Vamos supor que eu crie um sistema de apostas esportivas que exija apostas de US$ 1.000 para gerar um retorno de US$ 80.000 por ano. Para alcançar esse retorno, seriam necessárias aproximadamente 250 a 300 apostas por ano. As casas de apostas eventualmente me baniriam, da mesma forma que os cassinos banem os contadores de cartas? É possível se tornar um apostador esportivo bem-sucedido abertamente, ou é preciso agir às escondidas como um contador de cartas?
Primeiramente, duvido que alguém consiga ganhar 80 mil dólares com apostas de 1 mil dólares e uma banca de apenas 250 a 300 dólares. E nem me fale sobre a palavra "sistema". Respondendo à sua pergunta, na maioria das vezes, os melhores apostadores esportivos praticam abertamente. Mesmo que uma casa de apostas proibisse a atuação de um profissional ou o banisse do estabelecimento, seria fácil encontrar outra pessoa para fazer as apostas. Por outro lado, certa vez participei de um seminário sobre apostas especiais no Super Bowl ministrado por Fezzik, um apostador profissional, e ele fez a apresentação usando uma máscara de Halloween.
Você tem alguma dica para escolher o dígito final nos bolões do Super Bowl?
Nos bolões que eu vi, as tabelas eram randomizadas atribuindo um dígito aleatório a cada linha e coluna. No entanto, se você puder escolher os dígitos finais, a tabela a seguir mostra a frequência de cada dígito final para o placar final de cada time, com base em todos os jogos da NFL de 1983 a 2003.
Dígitos do terminal da NFL por lado
Dígito | Freqüência | Probabilidade |
0 | 1887 | 17,75% |
1 | 1097 | 10,32% |
2 | 348 | 3,27% |
3 | 1382 | 13,00% |
4 | 1608 | 15,13% |
5 | 396 | 3,73% |
6 | 848 | 7,98% |
7 | 1945 | 18,30% |
8 | 631 | 5,94% |
9 | 488 | 4,59% |
Total | 10630 | 100% |
Portanto, esta tabela mostra que 7 é a melhor opção, seguida por 0, 4 e 3.
Adoraria ver mais detalhes sobre seu modelo numérico de "palpites da NFL" . Aliás, se você começar a usar isso para fazer apostas de verdade, não seria considerado um "sistema de apostas"?
Algumas delas eu gosto mais do que outras. Meu modelo cria o que estima ser uma distribuição justa em cada jogo e eu listo aquelas que têm uma disparidade maior do que um número escolhido de pontos. Pessoalmente, aposto mais nas que têm as maiores disparidades. No entanto, até que eu prove que minhas escolhas são boas, acho que seria pretensioso publicar graus de confiança.
Com relação às suas escolhas na NFL, elas têm todas o mesmo peso, ou seja, alguma das escolhas é mais forte que as outras de acordo com o seu modelo?
Algumas delas eu gosto mais do que outras. Meu modelo cria o que estima ser uma distribuição justa em cada jogo e eu listo aquelas que têm uma disparidade maior do que um número escolhido de pontos. Pessoalmente, aposto mais nas que têm as maiores disparidades. No entanto, até que eu prove que minhas escolhas são boas, acho que seria pretensioso publicar graus de confiança.
Você é torcedor dos Packers de coração? Eu sou. Parece que você está apostando com o coração e os Packers estão arruinando suas ótimas apostas na NFL . Ótima porcentagem mesmo com os Packers não dando certo para você. Só achei que você gostaria da observação.
O motivo não tem nada a ver com lealdade à equipe. Meu programa os classificou como o quinto melhor time ao final da temporada de 2004, e mantive essa classificação para a temporada de 2005. No entanto, talvez seja uma reação lenta demais ao histórico recente. Algo para eu refletir.
Vi alguém oferecer 2 para 1 contra um jogador que acertou 57% dos jogos contra o spread em 100 partidas. Embora eu ache 57% um número difícil, considerando a pequena amostra, acredito que possa ser uma boa aposta. Minha pergunta é a seguinte: se o apostador tivesse um aproveitamento de 50% na carreira, ignorando a comissão e empates (ou seja, uma situação de cara ou coroa), essa seria uma boa aposta? Caso contrário, qual seria a porcentagem geral necessária para que o negócio fosse vantajoso para o apostador?
Para apostas de 2 para 1, o maior tamanho de amostra em que essa é uma boa aposta é de 14 jogos. Escolhendo aleatoriamente, você teria 39,5264% de chance de acertar 57% ou mais dos resultados, ou seja, 8 ou mais. Você precisa de uma probabilidade superior a 33,3333% para que seja uma boa aposta. 21 é um número próximo do justo, mas a probabilidade é ligeiramente baixa, de 33,1812%. Quanto maior o número de palpites necessários, menor deve ser a porcentagem exigida. Por exemplo, se fossem necessários 1000 palpites, o maior número necessário para ter mais de 1/3 de chance de ganhar seria 507. A probabilidade de acertar 507 ou mais resultados em 1000 palpites é de 34,05%.
Sou fã de futebol há muito tempo e também gosto de apostar. Estou muito interessado no seu modelo numérico para futebol e estou tentando criar o meu próprio, já que sei que não consigo ganhar apostando em futebol apenas com o meu conhecimento (já tentei). Então, resolvi experimentar uma abordagem estatística. Estou usando o programa estatístico SPSS. Minha pergunta é: quais variáveis você está usando no seu modelo?
Os únicos fatores que entram no modelo são as pontuações e a vantagem de jogar em casa. Às vezes, busco opiniões externas sobre lesões importantes, como a de Ben Roethlisberger na semana 6, ou sobre o New Orleans Saints jogando em casa em San Antonio.
Bem-vindo de volta, Mago! Você não é mais apenas o Mago das Probabilidades, mas, pelo seu desempenho, também é o Mago dos Palpites da NFL . Estou com apenas 51,7% de acerto no bolão do cassino. Tenho um pedido simples: seria possível listar seus palpites para TODOS OS JOGOS a cada semana, se não for muito incômodo?
Obrigado. Você provavelmente enviou isso antes da quarta semana, que foi uma semana ruim para mim. Agora, depois de cinco semanas, meu retrospecto é de 17 vitórias e 13 derrotas, com uma média de 56,7%, o que é bom, mas não ótimo. Acho que, como um bônus para os leitores da minha newsletter, vou compartilhar minhas impressões sobre todos os jogos.
Já que você está falando de futebol americano agora, tenho uma pergunta sobre apostas combinadas. Recentemente, fiz uma aposta em que escolhi o total de pontos (mais/menos) em cada um dos quatro quartos do jogo Steelers/Chargers Monday Night Football e ganhei. (Apenas quartos, sem considerar metade ou total.) Agora, a casa de apostas não quer pagar porque dizem que há correlação — que ganhar em um quarto aumenta a probabilidade de eu ganhar em outro. Acredito que cada quarto de um jogo seja mutuamente exclusivo, mas eles discordam. O que você acha?
Primeiro, quem aceitou essa aposta deve honrá-la, por princípio. Um cavalheiro honra suas dívidas, especialmente as de jogo. Segundo, embora eu não tenha estudado o assunto, acredito que os quartos possam ter uma correlação negativa. Por exemplo, se o primeiro quarto tiver uma pontuação baixa, é mais provável que uma das equipes esteja em boa posição de campo no início do segundo quarto, e, portanto, com maior probabilidade de ter uma pontuação alta no segundo quarto, e vice-versa.
Mago, tenho uma dúvida sobre minha porcentagem de acertos "real" em palpites da NFL . Digo aos meus amigos que não tive uma temporada perdedora nos últimos 5 anos (o que é verdade), apostando das semanas 3 a 16 com uma média de 2 a 3 palpites por semana. O meu lance é que tenho um ótimo feeling para os jogos e aposto bem mais naqueles em que acredito que as probabilidades estão a meu favor. Por exemplo, fiz 9 apostas este ano, 4 delas de US$ 55, acertando 3. Fiz 3 apostas de US$ 110, ganhando 1 delas. Mas adorei dois jogos em que apostei US$ 330 em um e US$ 600 (linha de 1/1), e ganhei ambos. Com certeza, estou com 6 de 9, o que dá 66% de aproveitamento, mas como acertei nos jogos em que tinha mais certeza, isso na realidade significa cerca de 80% de aproveitamento (em termos financeiros). Faz sentido para você? Descobri que, aproximadamente, consegui fazer isso ao calcular os últimos 5 anos (60-70% em palpites, mas cerca de 80% considerando o valor apostado). Você poderia me indicar uma maneira fácil de incluir o valor apostado nesse cálculo e confirmar se minhas suposições estão corretas? Muito obrigado.
Tenho pensado muito sobre isso ultimamente. Na minha opinião, a porcentagem de acertos deve ter o mesmo peso em cada jogo. Você também deve ter uma estatística separada sobre o seu retorno geral do investimento, porém qualquer estatística deve ser respaldada por uma lista com o lado, a data, a fonte da linha, o spread de pontos e as odds (geralmente -110). Outra questão que você não mencionou é o que fazer se tiver que apostar contra -120 em um spread de 3 ou 7 pontos. Seria mais fácil atingir uma boa porcentagem de acertos se você incluísse essas apostas em suas apostas. Portanto, acredito que uma métrica de retorno sobre o investimento deva ser mantida mesmo em apostas fixas. Outra coisa que me incomoda em alguns outros apostadores é que eles citam linhas que não estão disponíveis. Acho que pesquisar um pouco é válido, mas as linhas citadas não deveriam ser difíceis de encontrar. Admito que não faço algumas dessas coisas nesta temporada, porque não pensei nisso quando comecei. No próximo ano, se eu fizer isso novamente, também documentarei meus resultados como um investimento.
Você recomenda apostar na linha de dinheiro ou no spread em suas escolhas na NFL , ou tanto faz?
Independentemente do motivo da aposta, em geral é melhor apostar nos azarões na linha de dinheiro e nos favoritos contra o spread.
Sempre quis fazer minhas próprias análises de jogos da NFL, mas estou com dificuldade para encontrar um site, de preferência gratuito, para baixar dados históricos por time. Alguma sugestão? Arquivos para download seriam minha preferência, já que copiar e colar de uma página da web não é muito prático, mas eu faria isso se necessário. Além disso, informações como clima e condições do gramado seriam de grande ajuda.
Pessoalmente, eu uso o banco de dados NFL Access do Mr. NFL , que custa US$ 99. Se existe algo tão bom por menos, eu desconheço.
Seu sistema de palpites na NFL parece estar muito inclinado para o azarão. Em apenas 8 dos 49 jogos, você escolheu o favorito. Em um deles, você escolheu um time com odds iguais. Isso é uma falha no seu sistema ou as pessoas tendem a escolher favoritos e seu sistema está tentando se aproveitar dessa tendência? Não fiz uma análise, mas, pela minha observação, poucas apostas são ganhas na faixa de spread sem que o time vença a partida.
Historicamente falando, apostar nos azarões é uma opção melhor. Aqui estão os resultados de todos os jogos disputados desde o início da temporada de 1983 até a 10ª semana da temporada de 2005.
Vitórias do favorito contra o spread: 2554 jogos
Vitórias do azarão contra o spread: 2724 jogos
O jogo termina exatamente no spread: 150 jogos
Assim, em apostas resolvidas, o azarão venceu 51,61% das vezes. Também é sabido que os apostadores que apostam no "quadrado" preferem apostar nos favoritos, criando valor nas apostas nos azarões.
Este ano, nosso "Apostador de Futebol" aumentou a comissão nas apostas de mais/menos de 10% para 20% e eliminou a comissão de 10% nas apostas combinadas. Então, este ano, em vez de fazer duas apostas separadas de mais/menos, tenho combinado as duas apostas com um pagamento de 2,5 para 1. Essa é uma boa estratégia?
O retorno esperado nas apostas simples seria (0,5*1 + 0,5*(-1,2))/1,2 = -8,33%. O retorno esperado na aposta combinada seria 0,25*2,5 + 0,75*-1 = -12,5%. No entanto, se eu fosse apostar apenas em dois jogos e quisesse ganhar ou perder tudo, optaria pela aposta combinada. Mais importante ainda, eu boicotaria essa casa de apostas por princípio, pois nunca ouvi falar de ter que pagar -120 em apostas simples.
Em duas seções diferentes do seu site, você menciona que, em geral, é melhor apostar nos azarões do que nos favoritos contra a linha de dinheiro. No entanto, como você aponta no Apêndice 3 de Apostas Esportivas, a vantagem da casa na linha de dinheiro é MENOR ao apostar no favorito. Isso não é uma contradição? Não é verdade que, em qualquer tipo de aposta, o ideal é buscar a menor vantagem da casa possível?
Boa observação. Depois de refletir um pouco, decidi remover meu apêndice 3 sobre apostas esportivas. Ele se baseava na premissa de que a linha justa estaria exatamente entre as duas linhas de dinheiro. Por exemplo, no último Super Bowl, as linhas de dinheiro eram geralmente Seattle +160 e Pittsburgh -180. Meu apêndice partia da premissa irrealista de que as linhas de dinheiro justas seriam +/- 170. Na realidade, as linhas de dinheiro são determinadas pelo mercado. Apostas equilibradas na linha de dinheiro tendem a favorecer o favorito, criando valor no azarão. Considerando que Pittsburgh fosse favorito por 4 pontos, os dados históricos sugerem que um favorito por 4 pontos tem cerca de 61% de chance de vencer. Isso tornaria as linhas de dinheiro justas +156 para Seattle e -156 para Pittsburgh. Lembrando que a maioria dos cassinos tinha as linhas de dinheiro em +160/-180. Claro que Pittsburgh venceu o jogo desta vez, mas historicamente falando, tenho certeza de que você teria um retorno melhor apostando nos azarões na linha de dinheiro do que nos favoritos.
Estou participando de um bolão da NFL e tirei números muito bons: 7 e 4 para Pittsburgh e 4 e 0 para Seattle. Gostaria de saber qual a probabilidade de eu ganhar este ano?
Para os meus leitores que talvez não tenham entendido a pergunta, um bolão do Super Bowl tem uma grade de 10 por 10. Os jogadores compram quadrados por um valor fixo cada, escrevendo o nome do comprador em cada quadrado. Depois que todos os 100 quadrados forem comprados, as linhas e colunas devem receber cabeçalhos aleatórios de 0 a 9. Algo parecido com uma tabuada de multiplicação de 10 por 10, só que com os cabeçalhos das linhas e colunas embaralhados aleatoriamente. Então, o último dígito do placar de cada time será usado para determinar o vencedor. O motivo do embaralhamento é que alguns dígitos finais são muito mais prováveis do que outros, como você verá abaixo. Por exemplo, quem ficasse com o quadrado "Seattle 0, Pittsburgh 1" teria ganhado o bolão, porque o placar final foi Seattle 10, Pittsburgh 21.
A tabela a seguir mostra a frequência de cada combinação em todos os jogos da NFL das temporadas de 1983 a 2005. Deve-se notar que a regra da conversão de dois pontos foi introduzida por volta de 1998, o que teria o efeito de suavizar um pouco a distribuição.
Dígito terminal na NFL - Total de jogos fora de casa
| Time visitante | Time da casa | Total | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 0 | 126 | 104 | 34 | 160 | 138 | 37 | 99 | 237 | 64 | 32 | 1031 |
| 1 | 73 | 40 | 17 | 41 | 103 | 21 | 36 | 117 | 67 | 31 | 546 |
| 2 | 25 | 15 | 1 | 20 | 30 | 9 | 13 | 33 | 9 | 12 | 167 |
| 3 | 194 | 69 | 33 | 66 | 102 | 40 | 102 | 132 | 43 | 40 | 821 |
| 4 | 122 | 133 | 27 | 78 | 108 | 27 | 48 | 215 | 59 | 35 | 852 |
| 5 | 32 | 12 | 12 | 21 | 21 | 9 | 13 | 36 | 22 | 5 | 183 |
| 6 | 91 | 47 | 17 | 75 | 57 | 7 | 28 | 57 | 25 | 39 | 443 |
| 7 | 217 | 115 | 35 | 135 | 195 | 47 | 65 | 125 | 69 | 47 | 1050 |
| 8 | 43 | 59 | 12 | 24 | 41 | 23 | 20 | 38 | 15 | 7 | 282 |
| 9 | 48 | 28 | 17 | 33 | 40 | 14 | 29 | 33 | 14 | 7 | 263 |
| Total | 971 | 622 | 205 | 653 | 835 | 234 | 453 | 1023 | 387 | 255 | 5638 |
A próxima tabela mostra a probabilidade de cada combinação com base nos totais da tabela acima.
Dígito terminal na NFL — Probabilidade de jogo fora de casa contra jogo fora
| Time visitante | Time da casa | Total | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 0 | 0,0223 | 0,0184 | 0,006 | 0,0284 | 0,0245 | 0,0066 | 0,0176 | 0,042 | 0,0114 | 0,0057 | 0,1829 |
| 1 | 0,0129 | 0,0071 | 0,003 | 0,0073 | 0,0183 | 0,0037 | 0,0064 | 0,0208 | 0,0119 | 0,0055 | 0,0968 |
| 2 | 0,0044 | 0,0027 | 0,0002 | 0,0035 | 0,0053 | 0,0016 | 0,0023 | 0,0059 | 0,0016 | 0,0021 | 0,0296 |
| 3 | 0,0344 | 0,0122 | 0,0059 | 0,0117 | 0,0181 | 0,0071 | 0,0181 | 0,0234 | 0,0076 | 0,0071 | 0,1456 |
| 4 | 0,0216 | 0,0236 | 0,0048 | 0,0138 | 0,0192 | 0,0048 | 0,0085 | 0,0381 | 0,0105 | 0,0062 | 0,1511 |
| 5 | 0,0057 | 0,0021 | 0,0021 | 0,0037 | 0,0037 | 0,0016 | 0,0023 | 0,0064 | 0,0039 | 0,0009 | 0,0325 |
| 6 | 0,0161 | 0,0083 | 0,003 | 0,0133 | 0,0101 | 0,0012 | 0,005 | 0,0101 | 0,0044 | 0,0069 | 0,0786 |
| 7 | 0,0385 | 0,0204 | 0,0062 | 0,0239 | 0,0346 | 0,0083 | 0,0115 | 0,0222 | 0,0122 | 0,0083 | 0,1862 |
| 8 | 0,0076 | 0,0105 | 0,0021 | 0,0043 | 0,0073 | 0,0041 | 0,0035 | 0,0067 | 0,0027 | 0,0012 | 0,05 |
| 9 | 0,0085 | 0,005 | 0,003 | 0,0059 | 0,0071 | 0,0025 | 0,0051 | 0,0059 | 0,0025 | 0,0012 | 0,0466 |
| Total | 0,1722 | 0,1103 | 0,0364 | 0,1158 | 0,1481 | 0,0415 | 0,0803 | 0,1814 | 0,0686 | 0,0452 | 1 |
Embora exista um time da casa simbólico no Super Bowl, acho que podemos ignorar isso. Vamos também ignorar tudo sobre ambos os times e nos basear estritamente nas médias históricas acima. Finalmente, vamos ignorar o fato de que o Super Bowl não pode terminar empatado, o que tornaria uma partida como 4/4 um pouco menos provável de ser vencida. Então, vamos calcular a média quando os dígitos finais forem diferentes. Por exemplo, a probabilidade do seu quadrado "Pittsburgh 7, Seattle 4" seria a média de "Visitante 7, Casa 4" e "Visitante 4, Casa 7". Fazendo isso, obtemos a seguinte probabilidade para cada um dos seus quadrados.
Pitts 7, Mar 4: (0,0346+0,0381)/2 = 0,0364
Pitts 7, Mar 0: (0,0385+0,0420)/2 = 0,0403
Pitts 4, Mar 4: 0,0192
Pitts 4, Mar 0: (0,0216+0,0245)/2 = 0,0231
Portanto, sua probabilidade total de ganhar um desses é de 11,90%. Considerando que você cobriu apenas 4% dos quadrados, você se saiu bem.
Embora você não tenha perguntado especificamente, aqui está a frequência com que cada dígito terminal ocorreu. Isso mostra que, no geral, do mais frequente para o menos frequente, a ordem é 7043168952.
Dígito terminal na NFL — Totais fora e em casa
| terminal Dígito | Time visitante | Time da casa | Total |
|---|---|---|---|
| 0 | 1031 | 971 | 2002 |
| 1 | 546 | 622 | 1168 |
| 2 | 167 | 205 | 372 |
| 3 | 821 | 653 | 1474 |
| 4 | 852 | 835 | 1687 |
| 5 | 183 | 234 | 417 |
| 6 | 443 | 453 | 896 |
| 7 | 1050 | 1023 | 2073 |
| 8 | 282 | 387 | 669 |
| 9 | 263 | 255 | 518 |
Finalmente, aqui está a probabilidade de cada dígito terminal.
Dígito terminal na NFL — Probabilidades de jogos em casa e fora
| terminal Dígito | Time visitante | Time da casa | Total |
|---|---|---|---|
| 0 | 0,1829 | 0,1722 | 0,1775 |
| 1 | 0,0968 | 0,1103 | 0,1036 |
| 2 | 0,0296 | 0,0364 | 0,033 |
| 3 | 0,1456 | 0,1158 | 0,1307 |
| 4 | 0,1511 | 0,1481 | 0,1496 |
| 5 | 0,0325 | 0,0415 | 0,037 |
| 6 | 0,0786 | 0,0803 | 0,0795 |
| 7 | 0,1862 | 0,1814 | 0,1838 |
| 8 | 0,05 | 0,0686 | 0,0593 |
| 9 | 0,0466 | 0,0452 | 0,0459 |
Para mais informações sobre este tópico, visite Football Squares Mathematical and Statistical Strategy .
Existe um equívoco comum de que os limites de apostas esportivas em Las Vegas são muito altos, o que, na minha experiência, só se aplica ao futebol americano e nem sempre. Você poderia me informar os limites aproximados nas casas de apostas esportivas de Las Vegas para os quatro principais esportes? Agradeço a sua atenção.
Não considero o hóquei um esporte importante porque tem pouca movimentação. Me disseram que os cassinos da Costa têm os limites mais altos. Não há um limite máximo definido que eu saiba, mas eles aceitam apostas altas caso a caso. Aqui está o que eu acho que eles provavelmente aceitariam em uma partida média.
Lado da NFL: US$ 50.000
Total da NFL: US$ 5.000
Linha de dinheiro da MLB: US$ 10.000
Total da MLB: US$ 2.000
Lado da NBA: US$ 10.000
Total da NBA: US$ 2.000
Com muitas casas de apostas online oferecendo apostas no intervalo, gostaria de saber sua opinião sobre o "dutching". Às vezes é óbvio, mas em que momento você consideraria apostar o oposto da sua aposta inicial no intervalo? Além disso, qual valor você consideraria apostar se encontrasse uma situação favorável?
Suponho que por "dutching" você queira dizer cobertura. O sexto dos meus dez mandamentos do jogo é "Não farás cobertura em tuas apostas". A única exceção que eu faria seria quando a própria aposta de cobertura tivesse um valor esperado positivo, ou quando quantias de dinheiro que pudessem mudar a vida de alguém estivessem em jogo.
Qual o valor máximo que posso ganhar em uma aposta de futebol americano universitário em um cassino de Las Vegas sem precisar fornecer minhas informações pessoais ao cassino ao resgatar meu bilhete? Gostaria de saber o valor que posso ganhar (por aposta) e ainda receber o pagamento em dinheiro sem perguntas.
US$ 10.000. Uma transação em dinheiro superior a US$ 10.000, seja em esportes ou não, exigirá um CTR (relatório de transação em dinheiro). Você também pode solicitar o pagamento em fichas, embora o mesmo CTR seja gerado caso você as troque por dinheiro.
Além dos sites gratuitos, você pode recomendar um site onde eu possa obter análises esportivas profissionais mediante uma taxa mensal ou uma porcentagem de acerto?
Não. Eu não endosso nenhum cambista.
Você mencionou suas apostas nos azarões da NFL. Você simplesmente apostava no azarão jogando em casa todas as vezes ou era algo mais complexo do que isso? E, mais importante, qual linha determinava se era um azarão jogando em casa... A linha inicial ou a linha pouco antes do jogo? Obrigado.
Eu não aposto cegamente em azarões, mesmo que tenha que pagar apenas -105, como é o caso nesta temporada no Plaza, no centro de Las Vegas. Se eu detectar uma pequena vantagem em uma aposta esportiva, não aposto. Em esportes, sempre considero uma certa margem de erro, porque, no fim das contas, são as pessoas que jogam, não as estatísticas. No entanto, se eu encontrar uma linha melhor do que a do mercado, ou se a aposta vier com a recomendação de um especialista confiável, então terei prazer em fazer a aposta.
Obrigado pelo excelente site! Meu pai e eu estamos discutindo sobre apostas de cobertura e sua ajuda seria muito bem-vinda! A situação em questão envolve uma aposta no Super Bowl. Antes do início da temporada (meu pai não se lembra do ano), meu tio apostou que o New England Patriots venceria o Super Bowl. A aposta pagou 60 para 1. Pouco antes do Super Bowl (no qual o New England Patriots estava jogando), meu tio fez uma cobertura na aposta (meu pai não se lembra dos detalhes), abrindo mão do potencial prêmio de US$ 6.000, mas garantindo um prêmio de US$ 3.000. Estou convencido de que essa foi uma aposta furada, mas meu pai não me ouve. Argumento que, ao fazer a cobertura nesse momento, ele estava abrindo mão do valor esperado, e um apostador inteligente nunca faz isso. Meu pai argumenta que não há problema em abrir mão do valor esperado devido ao dinheiro envolvido e ao fato de que essa aposta não acontece com frequência, exatamente como fazer um seguro residencial. É claro que defendo que a propriedade de uma casa é inerentemente diferente das apostas esportivas, pois uma pode ser evitada enquanto a outra é praticamente inevitável. Qual a sua opinião? Ajude-nos a resolver essa questão!
O sétimo dos meus Dez Mandamentos do Jogo é: "Não farás apostas seguras". No entanto, em meus comentários, acrescento: "Exceções podem ser feitas para assegurar quantias de dinheiro que mudam a vida". Portanto, se o valor de resgate de US$ 3.000 representa uma quantia que muda a vida dele, e se a probabilidade de ganhar não fosse muito superior a 50%, então eu não criticaria sua decisão. Contudo, a menos que isso tenha ocorrido em 2002, a probabilidade de o New England vencer era muito maior que 50%. Nos outros dois anos em que jogaram no Super Bowl, 2004 e 2005, eram favoritos por 7 pontos. Eu estimaria que a probabilidade de vencer em qualquer um desses anos era de cerca de 71%. Um valor de resgate justo teria sido 0,71 × US$ 6.100 (incluindo sua aposta original de volta) = US$ 4.331. A vantagem da casa na oferta, que era equivalente a uma aposta de 1 para 1 no outro time, era de 29% - 71% = 42%. Então, se eu estiver certo sobre o ano, ele tomou uma decisão muito ruim. Ele poderia ter conseguido odds muito melhores no mercado aberto apostando na vitória do outro time. Quem ofereceu apenas US$ 3.000 ou era muito ignorante sobre o jogo ou se aproveitou da situação de forma injusta. Curiosamente, o New England venceu todos os seus três Super Bowls recentes por três pontos.
Qual a probabilidade de um jogo da NFL terminar empatado?
Entre as temporadas de 1983 e 2007, ocorreram 10 empates em 5.901 jogos da temporada regular. As regras determinam que um jogo não pode terminar empatado nos playoffs. Portanto, com base em jogos históricos, a probabilidade seria de 0,17%, ou cerca de 1 em 590.
Qual é o desvio padrão da diferença entre o saldo de pontos final entre as duas equipes em um jogo da NFL e o spread de pontos desse jogo?
Para o benefício de outros leitores, vejamos um exemplo do último Super Bowl para ilustrar sua pergunta. Os Patriots eram favoritos por 12 pontos, mas perderam por 3. Portanto, o jogo terminou com uma diferença de 15 pontos em relação ao spread. Se entendi corretamente a pergunta, você está perguntando sobre o desvio padrão dessa diferença. A diferença média foi próxima de zero para cada liga estudada. Aqui está o que obtive para o desvio padrão:
NFL 13.31 (com base nas temporadas de 2000 a 2007)
Futebol americano universitário: 15,72 (com base nas temporadas de 1993 a 2007)
NBA 11,39 (com base nas temporadas de 1987 a 2003)
Assim, o Super Bowl de 2008 terminou 15/13,31 = 1,13 desvios padrão abaixo do esperado. Estou ignorando o fator de ajuste para uma distribuição discreta, para manter as coisas o mais simples possível. A probabilidade de estar a 1,13 desvios padrão ou mais do esperado, em qualquer direção, é de 25,85%. Isso pode ser encontrado no Excel, usando a fórmula 2 × DIST.NORM(-1,13).
Como apostador esportivo, que gosta de apostar nos azarões e de comparar as odds, sei o valor de encontrar cada meio ponto extra possível. Em um jogo típico da NFL ou da NBA, quanto vale cada meio ponto para você? Sei que um apostador com odds de -110 em uma linha justa precisa acertar 52,4% das apostas para não ter prejuízo. Sei que as linhas são ditadas pelo mercado, mas quanto você diria que cada meio ponto realmente vale? Se você conseguisse meio ponto extra na linha justa de cada jogo em que aposta, isso faria com que seu ponto de equilíbrio fosse realmente de 50%? Existe alguma maneira de calcular isso? Obrigado.
Como mostro na minha página sobre a NBA , ao comprar meio ponto, a probabilidade de vitória é de 51,01%, a de derrota é de 47,01% e a de empate é de 1,98%, assumindo que o apostador nunca compre o meio ponto com um spread de 0 ou -1, o que não deveria fazer. Se você tivesse que apostar apenas 110 para obter o meio ponto extra, o retorno esperado seria (0,5101 - 1,1 × 0,4701) / 1,1 = -0,64%. Portanto, meio ponto grátis não seria suficiente para compensar a vantagem da casa.
Você não perguntou, mas se você apostar contra 120, pode comprar meio ponto na maioria das casas de apostas. Se você já estava disposto a apostar contra o spread, vale a pena comprar meio ponto extra? Apostando contra 110, a vantagem da casa para um apostador aleatório é de 4,45%, incluindo empates. Apostando contra 120, a vantagem da casa com o meio ponto é de 4,50%. Portanto, comprar meio ponto não compensa o preço.
O valor de apostar em meio ponto no futebol americano depende muito da diferença de pontos, pois algumas margens de vitória são muito mais prováveis do que outras. A única situação em que vale a pena apostar em meio ponto na NFL é quando a diferença de pontos é de 3. Infelizmente, as casas de apostas também sabem disso e, na maioria das vezes, não permitem apostas com diferença de 3.
Sabendo que o time A marca em média 1,5 gols por jogo e o time B marca em média 1,2 gols por jogo, qual a probabilidade de que em uma partida entre A e B:
1) A marcará mais pontos que B.
2) B terá uma pontuação maior que A.
3) O jogo termina empatado.
As informações fornecidas são suficientes para calcular as probabilidades de cada resultado?
Isso não leva em consideração que as pontuações individuais devem ter uma correlação negativa, e que a média de pontos que cada time cede é tão importante quanto a média de pontos marcados. Se pudermos assumir que 1,5 e 1,2 são os números esperados de pontos marcados na partida, considerando tanto o ataque quanto a defesa, e ignorarmos o fator de correlação, então podemos obter uma estimativa razoável para suas três probabilidades. Existem muitas apostas semelhantes para o Super Bowl, baseadas em quem marcará mais touchdowns, field goals, interceptações, etc.
O primeiro passo é usar a distribuição de Poisson para estimar a probabilidade de cada número de gols para cada equipe. A fórmula geral para a probabilidade de uma equipe marcar g gols, com uma média de m, é e^ (- m × m ) / g!. No Excel, você pode usar a fórmula poisson(g,m,0). A tabela a seguir mostra a probabilidade de 0 a 10 gols para ambas as equipes, usando essa fórmula.
Probabilidades de 0 a 8 gols para cada equipe
| Metas | Equipe A | Equipe B |
| 0 | 0,223130 | 0,301194 |
| 1 | 0,334695 | 0,361433 |
| 2 | 0,251021 | 0,216860 |
| 3 | 0,125511 | 0,086744 |
| 4 | 0,047067 | 0,026023 |
| 5 | 0,014120 | 0,006246 |
| 6 | 0,003530 | 0,001249 |
| 7 | 0,000756 | 0,000214 |
| 8 | 0,000142 | 0,000032 |
O próximo passo é bastante mundano, mas você precisa criar uma matriz com todas as 81 combinações possíveis de pontuações de 0 a 8 para cada equipe. Isso é feito multiplicando a probabilidade de x pontuações para a equipe A pelas probabilidades de y pontuações para a equipe B, conforme a tabela acima. A tabela a seguir mostra a probabilidade de cada combinação de pontuação de 0-0 a 8-8.
A próxima tabela mostra o vencedor de acordo com cada combinação de gols, onde T representa um empate.
Combinações vencedoras para ambas as equipes
| Objetivos da Equipe A | Objetivos da Equipe B | ||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 0 | T | B | B | B | B | B | B | B | B |
| 1 | UM | T | B | B | B | B | B | B | B |
| 2 | UM | UM | T | B | B | B | B | B | B |
| 3 | UM | UM | UM | T | B | B | B | B | B |
| 4 | UM | UM | UM | UM | T | B | B | B | B |
| 5 | UM | UM | UM | UM | UM | T | B | B | B |
| 6 | UM | UM | UM | UM | UM | UM | T | B | B |
| 7 | UM | UM | UM | UM | UM | UM | UM | T | B |
| 8 | UM | UM | UM | UM | UM | UM | UM | UM | T |
Por fim, você pode usar a função SOMASE no Excel para somar as células correspondentes aos três resultados possíveis da aposta. Nesse caso, as probabilidades são:
A vence = 44,14%
B vence = 30,37%
Empate = 25,48%
O Apêndice C do livro "Sharp Sports Betting" de Stanford Wong apresenta as probabilidades de vitória, derrota e empate para apostas como essa. Para este caso específico, ele lista 44%, 30% e 25%. Se alguém souber uma fórmula simples para esse tipo de problema, ficarei muito grato.
Complemento: Recebi um e-mail do Bob P., que sempre me mantém alerta quando o assunto é matemática. Aqui está o que ele escreveu.
Pesquisei a distribuição da diferença entre duas distribuições de Poisson não correlacionadas. É uma distribuição de Skellam (novidade para mim).De qualquer forma, a questão pode então ser formulada como P(Z=0), P(Z>0) e P(Z<0), onde Z é um Skellam com parâmetros 1,5 e 1,2.
Se você ainda não fez isso, ficará feliz em saber
P(Empate) = P(Z=0) = 0,254817
P(A vence B) = P(Z>0) = 0,441465
P(B vence A) = P(Z<0) = 1 - 0,254817 - 0,441465 = 0,303718
Respostas quase idênticas às suas.
A entrada da Wikipédia sobre um Skellam menciona funções de Bessel , que é mais ou menos o ponto do cálculo em que eu fico com medo de ir mais longe. Então, vou confiar na palavra do Bob neste caso.
Tenho tido sorte apostando com times que vêm de uma sequência de 5 derrotas e contra times que vêm de 5 vitórias seguidas. Argumento que, diferentemente de dados e roleta, onde se diz que os dados ou a bola não têm memória, um time profissional de esportes não pode ganhar ou perder indefinidamente. Escolhi a sequência de 5 vitórias seguidas após analisar quando a mudança ocorreria com mais frequência. Não me importa onde eles estão jogando, quem é o arremessador titular, lesões, etc. Você acha que meu raciocínio está correto?
Acho que essas são boas apostas, mas não pelo motivo que você mencionou. Um time esportivo pode, em teoria, perder indefinidamente. Uma das razões pelas quais essas apostas são boas é que, na grande maioria das vezes, elas serão em times com grandes chances de vitória, e azarões geralmente são apostas mais fortes do que favoritos. Além disso, quem aposta no "equilibrado" geralmente aposta no resultado oposto nessas situações, criando valor para você.
Sou um dos seis participantes de um concurso de palpites da NFL. Cada um de nós precisa escolher 70 jogos ao longo da temporada, usando as odds de uma grande casa de apostas online, que oferecem uma linha de 20 centavos. Um dos outros participantes ofereceu uma aposta em "mais/menos" para o placar mais alto no final da temporada. A aposta dele gerou um lucro de 8,5 unidades. Vamos supor que a temporada ainda não começou e que os participantes sejam apostadores esportivos experientes. O que você acha dessa linha e como você a analisaria?
A grande questão a se fazer com uma aposta como essa é qual a probabilidade de uma determinada escolha terminar em vitória, derrota ou empate. Na minha seção sobre apostas na NFL , podemos ver que 2,8% dos jogos terminam exatamente na linha de aposta. Vamos considerar 3%, para simplificar. Vamos chamar de p a probabilidade de uma vitória, dado que a aposta foi resolvida. Para um apostador puramente aleatório, p seria obviamente 50%. É fácil melhorar isso escolhendo apenas os azarões. Como minha página mencionada anteriormente mostra, ao longo de 25 temporadas, apostar sempre nos azarões teria resultado em uma taxa de acerto de 51,5%. Também é fácil melhorar um pouco mais essa taxa escolhendo as linhas mais favoráveis contra o mercado em geral. Com essas duas opções, acho que não é difícil chegar a 52%. Então, vou confiar que esses caras podem chegar pelo menos a 52%.
Assim, assumindo que 52% das apostas resolvidas sejam vencedoras, as probabilidades gerais são:
Vitória: 50,44%
Empate: 3,00%
Perda: 46,56%
Usando estatísticas básicas, é fácil ver que o ganho esperado por palpite, apostando em -110, é de -0,0078. O desvio padrão por palpite é de 1,0333. O ganho esperado em 70 palpites é de -0,5432, e o desvio padrão é de 70 1/2 × 1,0333 = 8,6452. Um ganho de 8,5 unidades está 9,0432 unidades acima das expectativas, ou 9,0432/8,6452 = 1,0460 desvios padrão à direita das expectativas na Curva Gaussiana. Acho que podemos ignorar o ajuste para uma distribuição discreta devido aos empates, e alguns jogos que não são -110/-110 resultarão em uma curva bastante suave, com uma queda de um fator de 0,05 unidades.
Portanto, a probabilidade de qualquer jogador terminar com uma pontuação superior a 1,046 desvios padrão acima do esperado é de 14,77%. Esse valor pode ser encontrado em qualquer tabela da curva gaussiana ou com a fórmula =1-dist.norm(1,046) no Excel. A probabilidade de todos os seis jogadores terminarem com uma pontuação inferior a 1,046 desvios padrão é (1-0,1477) ⁶ = 38,31%. Assim, a probabilidade de pelo menos um jogador terminar com uma pontuação superior a 1,046 desvios padrão é de 61,69%. Isso faz com que a aposta no "mais de" pareça uma aposta sólida com odds de -110. Mostro que é justa com odds de -161.
A tabela a seguir mostra a probabilidade de a aposta "mais de 8,5" vencer, considerando vários valores de p. Talvez a pessoa que definiu a aposta estivesse assumindo um valor mais próximo de 51% para p.
Aposta de handicaps da NFL
| Prob. Escolha correta | Probabilidade de vitórias acima de |
| 50,0% | 41,16% |
| 50,5% | 46,18% |
| 51,0% | 51,33% |
| 51,5% | 56,53% |
| 52,0% | 61,69% |
| 52,5% | 66,72% |
| 53,0% | 71,52% |
O que você acha da decisão dos Patriots de tentar a primeira descida quando estavam na quarta descida na linha de 28 jardas do próprio campo — e vencendo por 6 pontos?! Quais as chances de conseguir uma primeira descida nessa situação, e o que você teria feito?
Para benefício dos demais leitores, isso se refere a um jogo de 15 de novembro de 2009 , no qual os Patriots venciam os Colts por seis pontos. Faltava 1 minuto e 57 segundos para o fim do quarto período, era quarta descida e cerca de 1,5 jarda para avançar, com a bola na linha de 28 jardas dos Patriots. O técnico dos Patriots, Bill Belichick, tomou a agora controversa decisão de garantir a vitória e tentar a primeira descida na quarta descida curta, em vez de adiar a jogada e chutar a bola para longe.
Há uma ótima coluna sobre isso no Las Vegas Review Journal . Ela cita o apostador profissional e também atuário Steve Fezzik, dizendo que as probabilidades favoreciam a tentativa de primeira descida. Concordo plenamente. Em geral, acho que outros treinadores chutam a bola para fora do campo com muita frequência e têm muito medo de arriscar. Para defender meu ponto de vista, perguntei ao meu amigo e apostador esportivo Joel B., que é muito melhor do que eu em analisar probabilidades de futebol americano durante o jogo. Ele me ofereceu as seguintes probabilidades:
- Probabilidade do Patriot conseguir a primeira descida: 60%
- Probabilidade de vitória dos Patriots, caso consigam a primeira descida: 100%
- Probabilidade de vitória dos Patriots, caso não consigam a primeira descida: 50%
- Probabilidade de vitória dos Patriots, caso optem por chutar a bola para fora do campo: 75%
Portanto, a probabilidade de vencer tentando a primeira descida é de 60% × 100% + 40% × 50% = 60% + 20% = 80%. Isso é maior do que os 75% de probabilidade de vencer chutando a bola para longe.
Os críticos de plantão podem demonizar Belichick o quanto quiserem, mas eu aplaudo sua decisão. Ele não deve ser julgado pelo resultado do jogo, mas sim por se as probabilidades estavam a seu favor naquele momento. Acredito firmemente que estavam. Uma semana depois, no jogo entre Ravens e Steelers, os Ravens arriscaram na quarta descida para cinco jardas e conseguiram. Embora fosse uma situação diferente, ainda não ouvi ninguém questionar essa decisão.
Em prol da imparcialidade, estou fornecendo um link para um artigo que apresenta o ponto de vista oposto, intitulado "A quarta descida imprudente de Belichick", de Bill Simmons, no ESPN.com.
Suponha que haja dois jogos de futebol em que eu acredito que um dos jogadores tenha vantagem. Digamos que cada um tenha 55% de chance de vitória, e eu precise apostar contra 110. O que é mais lucrativo: apostar diretamente nos jogos ou fazer uma aposta combinada simples?
Boa pergunta. Resumindo, a vantagem por aposta é 0,55 × (10/11) - 0,45 = 0,05. Como uma aposta combinada, a vantagem é (0,55) ² × ((21/11) ² - 1) - (1 - (0,55) ² ) = 10,25%. Portanto, parece que a aposta combinada é a melhor maneira de maximizar a vantagem.
No entanto, a variância é maior em uma aposta combinada. Se você estiver seguindo o Critério de Kelly , precisará proteger seu saldo para a aposta combinada com uma aposta menor. Neste exemplo, a aposta ideal de Kelly para uma aposta simples é de 5,48% do saldo se os dois jogos coincidirem, 5,50% se o primeiro jogo terminar antes de você apostar no segundo e 3,88% para a aposta combinada. Multiplicando a aposta pela vantagem, obtemos 0,00275 para a aposta simples (com base em uma vantagem de 5,50%) e 0,00397 para a aposta combinada. Portanto, a aposta combinada resulta em um lucro maior.
Considerei o caso geral para esse tipo de pergunta, analisando também apostas combinadas de 3 e 4 equipes e apostas na linha de dinheiro. Assumindo uma pequena vantagem para todas as apostas, como regra geral, se a probabilidade de cada evento vencer for menor que 33%, você deve apostar diretamente. Se cada probabilidade estiver entre 33% e 52%, você deve fazer uma aposta combinada de 2 equipes. Se cada probabilidade estiver entre 52% e 64%, você deve fazer uma aposta combinada de 3 equipes. Se cada probabilidade for maior que 64%, você deve fazer uma aposta combinada de 4 equipes. Se você estiver fazendo apostas diretas, você terá praticamente o mesmo resultado fazendo apostas combinadas de 2 ou 3 equipes, assumindo novamente que você tenha uma vantagem inicial.
Devo ressaltar que, se você é um apostador recreativo que joga contra a vantagem da casa (qual apostador esportivo admitiria isso?), apostar diretamente minimiza a vantagem da casa.
Qual a probabilidade de realizar uma conversão de 2 pontos na NFL?
Nas temporadas da NFL de 2000 a 2009, excluindo os playoffs de 2009, houve 567 tentativas de conversão de dois pontos falhas e 318 tentativas bem-sucedidas. Com base nisso, a probabilidade de sucesso é de 318/(567+318) = 35,9%.
Gostei muito dos guias compactos e práticos do site Wizard of Vegas . Também tenho uma pergunta sobre o guia de apostas esportivas . O painel mostrado não exibe o total de pontos ou a linha de dinheiro para alguns jogos, então presumo que o cassino não oferecia essas apostas. Isso tem a ver com a diferença de pontos ou há algum outro motivo para elas não estarem lá?

Essa foto foi tirada em uma franquia da Leroy's, que é uma casa de apostas esportivas pequena e conservadora. Eles costumam divulgar primeiro o spread e, posteriormente, o total e as linhas de dinheiro.
Também é incomum oferecer apostas com odds muito desequilibradas, como por exemplo, Eastern Michigan vs. Central Michigan com uma diferença de 23 pontos. É difícil definir odds precisas para jogos assim, e o risco de apostas desequilibradas é maior. O melhor cassino para apostar com odds muito desequilibradas em jogos com grandes diferenças de pontos é o Hilton. Por fim, se a diferença de pontos for muito pequena, como 1 ou 1,5, a maioria das casas de apostas nem se dá ao trabalho de oferecer odds com odds muito desequilibradas, porque apostar contra o spread provavelmente resultaria no mesmo resultado.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Agradeço a oportunidade de ganhar um exemplar autografado do seu livro ao prever o placar exato do Super Bowl. No entanto, o valor esperado não é muito baixo? Calculo que a probabilidade de ganhar seja de cerca de 1 em 300.
Acho que as chances são melhores do que isso com um palpite bem fundamentado. Aqui está minha estratégia básica para acertar o resultado exato de qualquer jogo da NFL.
- Usando o total e o spread, estime o total de pontos de cada equipe. Por exemplo, se usarmos um total de 57 e um spread de -5 para o Super Bowl, considerando c = pontos dos Colts e s = pontos dos Saints, então...
(1) c+s=57
(2) c-5=s
Substituindo a equação (2) na equação (1):
c+(c-5)=57
2c-5=57
2c=62
c=31
s=31-5=26
O problema de parar por aqui é que, às vezes, você obtém valores que dificilmente serão alcançados por uma única equipe. Por exemplo, a probabilidade de uma equipe marcar 24 pontos é de 6,5%, mas a probabilidade de marcar 25 é de apenas 0,9%. A tabela abaixo mostra a probabilidade de uma equipe marcar 24 pontos, com base nas temporadas de 2000 a 2009. Portanto, vamos estimar o total de pontos para cada equipe com base em combinações realistas de field goals e touchdowns. - Suponha que o favorito marque 2 gols de campo.
- Suponha que o azarão marque um gol de campo.
- Subtraia os pontos dos field goals de cada um. No exemplo do Super Bowl, isso deixaria os Colts com 25 pontos de touchdown e os Saints com 23 pontos de touchdown.
- Divida os pontos de touchdown por 7 para obter a estimativa de touchdowns. c = 3,57 TD, s = 3,29 TD
- Arredonde o número estimado de touchdowns para o número inteiro mais próximo. c=4, s=3.
- Seguindo este método, obtemos para pontos totais c=(4×7)+(2×3)=34, s=(3×7)+(1×3)=24.
Utilizando esse método em todos os 6.707 jogos das temporadas de 1983 a 2009, teríamos obtido 69 palpites corretos, para uma taxa de sucesso de 1,03%. A última vez que teria acertado foi no jogo entre Titans e Colts na semana 13 de 2009. Naquele jogo, o spread era de Colts -6,5 e o total de pontos era 46. O placar foi Titans 17, Colts 27.
Um crítico sugeriu que uma estratégia melhor e mais simples seria escolher o total de pontos mais próximo entre as duas equipes. Utilizando esse método, obtivemos apenas 51 vitórias, o que representa uma taxa de acerto de 0,76%. Na minha opinião, dividir os pontos marcados em 2 para as equipes mais fortes e 1 para as mais fracas é importante.Totais de uma única equipe nas temporadas da NFL de 2000 a 2009
| Total de uma equipe | Total na amostra | Probabilidade |
| 0 | 93 | 1,75% |
| 1 | 0 | 0,00% |
| 2 | 0 | 0,00% |
| 3 | 148 | 2,79% |
| 4 | 0 | 0,00% |
| 5 | 2 | 0,04% |
| 6 | 114 | 2,15% |
| 7 | 210 | 3,96% |
| 8 | 9 | 0,17% |
| 9 | 76 | 1,43% |
| 10 | 316 | 5,96% |
| 11 | 9 | 0,17% |
| 12 | 49 | 0,92% |
| 13 | 289 | 5,45% |
| 14 | 238 | 4,49% |
| 15 | 55 | 1,04% |
| 16 | 170 | 3,21% |
| 17 | 373 | 7,03% |
| 18 | 33 | 0,62% |
| 19 | 92 | 1,73% |
| 20 | 368 | 6,94% |
| 21 | 234 | 4,41% |
| 22 | 64 | 1,21% |
| 23 | 218 | 4,11% |
| 24 | 347 | 6,54% |
| 25 | 47 | 0,89% |
| 26 | 103 | 1,94% |
| 27 | 282 | 5,32% |
| 28 | 159 | 3,00% |
| 29 | 52 | 0,98% |
| 30 | 127 | 2,39% |
| 31 | 242 | 4,56% |
| 32 | 23 | 0,43% |
| 33 | 57 | 1,07% |
| 34 | 164 | 3,09% |
| 35 | 76 | 1,43% |
| 36 | 27 | 0,51% |
| 37 | 68 | 1,28% |
| 38 | 108 | 2,04% |
| 39 | 11 | 0,21% |
| 40 | 21 | 0,40% |
| 41 | 62 | 1,17% |
| 42 | 31 | 0,58% |
| 43 | 6 | 0,11% |
| 44 | 24 | 0,45% |
| 45 | 33 | 0,62% |
| 46 | 1 | 0,02% |
| 47 | 7 | 0.13% |
| 48 | 28 | 0,53% |
| 49 | 15 | 0,28% |
| 50 | 1 | 0,02% |
| 51 | 5 | 0,09% |
| 52 | 7 | 0,13% |
| 53 | 0 | 0,00% |
| 54 | 2 | 0,04% |
| 55 | 1 | 0,02% |
| 56 | 4 | 0,08% |
| 57 | 1 | 0,02% |
| 58 | 1 | 0,02% |
| 59 | 1 | 0,02% |
| Total | 5304 | 100,00% |
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Qual a probabilidade de um chute curto ser bem-sucedido na NFL antes do quarto período? Quero dizer, a jogada no Super Bowl foi absolutamente genial, mas o técnico dos Saints tinha as estatísticas para embasar sua decisão, ou estava apenas seguindo um palpite?
De acordo com um excelente artigo no advancedfootballanalytics.com, a probabilidade histórica de sucesso é de 26%. No entanto, na maioria dos chutes curtos, o outro time espera por eles, o que diminui a probabilidade de sucesso. Para chutes curtos surpresa, a probabilidade de sucesso é de 60%! A ideia principal do artigo é que uma estratégia inteligente seria usar chutes curtos surpresa com mais frequência. Concordo; foi uma jogada brilhante dos Saints.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Que dinâmicas afetam as apostas em totais no futebol à medida que a temporada avança, o clima piora e há mais informações sobre o desempenho recente das equipes? Quão fácil (ou difícil) é encontrar erros nas linhas de apostas?
Para ajudar a responder a essa pergunta, elaborei um gráfico com a média de pontos marcados por semana na NFL, com base em todas as temporadas de 1983 a 2009. O gráfico a seguir mostra os resultados.
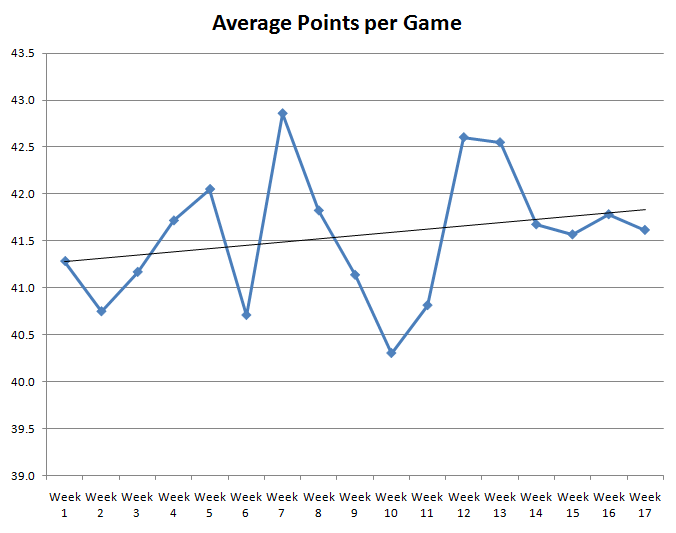
Como você pode ver, a linha oscila bastante. A linha preta fina é a linha de melhor ajuste por mínimos quadrados, que mostra uma tendência geral de alta. Portanto, conforme as estações avançam e as temperaturas caem, a média de pontos marcados aumenta ligeiramente, mas isso pode ser facilmente uma variação aleatória.
Isso é o máximo que posso dizer. Para uma opinião geral sobre como o clima afeta as apostas esportivas, recorri ao meu amigo Jason Been, que é especialista no assunto. Eis o que ele disse:
Na maioria dos casos, o vento é o principal fator climático que afeta um jogo; porém, não é o único. No beisebol e em outros esportes ao ar livre, as sombras podem ter um impacto semelhante, especialmente durante os jogos vespertinos do início e do fim da temporada. Chuva ou neve não são fatores tão relevantes no futebol americano quanto a maioria das pessoas pensa, pois geralmente afetam o ataque e a defesa igualmente. Um exemplo seria um defensor contra um recebedor. A chuva e a neve os atrasariam igualmente, não dando vantagem a nenhum dos lados. O vento pode simplesmente eliminar o jogo aéreo no futebol americano, assim como os chutes. Já vi jogos em que um time que priorizava o passe foi forçado a correr com a bola em quase todas as jogadas devido a um forte vento lateral. Não acontece com frequência, mas ocasionalmente o vento é o fator decisivo em uma partida.Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Na NFL, em média, qual é a probabilidade de que, após uma pontuação, o outro time seja o próximo a marcar?
Com base nas temporadas da NFL de 2000 a 2009, a resposta é 57%.
Se um time da NFL sofreu uma derrota acachapante no último jogo, é melhor apostar nele ou contra ele na próxima partida? A mesma pergunta se aplica a uma grande vitória. Ouço com frequência que, após uma derrota expressiva, um time "terá algo a provar", enquanto um time com uma grande vitória pode estar confiante demais e acomodado. Há alguma verdade nisso?
Demonstro que, após uma derrota por 21 pontos ou mais, a equipe cobrirá o spread em 51,66% das vezes. No entanto, isso está bem dentro da margem de erro. A tabela a seguir mostra os resultados em relação ao spread do último jogo, de acordo com a vitória ou derrota da mesma equipe no jogo anterior. Os resultados nunca se afastam muito de 50% e estão sempre dentro de um desvio padrão desse valor. Basicamente, não encontro correlação estatística entre a vitória/derrota em relação ao spread e quantos pontos a equipe ganhou ou perdeu no jogo anterior.
Vitória, derrota ou empate contra o spread de acordo com a margem de vitória ou derrota do jogo anterior.
| Resultado do jogo anterior | Vitória contra o spread | Perda contra spread | Empate contra spread | Taxa de vitórias | Desvio Padrão |
| Ganhe por 21 ou mais pontos. | 233 | 247 | 17 | 48,54% | 2,28% |
| Vitória por 14 a 20 | 235 | 219 | 11 | 51,76% | 2,35% |
| Vitória por 10 a 13 | 188 | 180 | 8 | 51,09% | 2,61% |
| Vitória por 7 a 9 | 198 | 181 | 12 | 52,24% | 2,57% |
| Vitória por 4 a 6 | 164 | 170 | 12 | 49,10% | 2,74% |
| Vitória por 3 | 202 | 212 | 14 | 48,79% | 2,46% |
| Derrota por 2 a vitória por 2 | 184 | 188 | 14 | 49,46% | 2,59% |
| Derrota por 3 | 209 | 207 | 12 | 50,24% | 2,45% |
| Derrota por 4 a 6 | 174 | 163 | 9 | 51,63% | 2,72% |
| Derrota por 7 a 9 | 187 | 195 | 9 | 48,95% | 2,56% |
| Derrota por 10 a 13 | 173 | 189 | 14 | 47,79% | 2,63% |
| Derrota por 14 a 20 | 220 | 232 | 15 | 48,67% | 2,35% |
| Derrota por 21 ou mais pontos | 249 | 233 | 15 | 51,66% | 2,28% |
Tabela baseada em todos os jogos da NFL, da semana 1 da temporada de 2000 até a semana 4 da temporada de 2010.
A casa de apostas Pinnacle passou a exibir suas odds em formato decimal. Como faço para converter as odds da casa de apostas do formato decimal para o formato americano?
Vejamos, por exemplo, o jogo de futebol americano da noite de segunda-feira, 25 de outubro de 2010. As probabilidades europeias são as seguintes:
New York Giants 2.750
Dallas Cowboys 1.513
Ambos os valores representam o que você receberá de volta por uma unidade apostada se ganhar, incluindo sua aposta inicial. Quando as probabilidades decimais são maiores ou iguais a 2, a conversão é simples: basta subtrair um e multiplicar por 100. Se as probabilidades forem menores que 2, então (1) subtrai-se 1, (2) inverte-se o resultado e (3) multiplica-se por -100.
Para quem prefere uma fórmula, se as probabilidades decimais pagam x, aqui está o cálculo para as probabilidades americanas equivalentes:
Se x>=2: 100*(x-1)
Se x<2: -100/(x-1)
No exemplo acima, as linhas no formato americano são:
New York Giants: 100*(2,750-1) = +175
Dallas Cowboys: -100/(1,513-1) = -195
Você também pode converter automaticamente todas as linhas selecionando "American Odds" no menu suspenso no canto superior esquerdo do site da Pinnacle, acima do logotipo.
Fiz uma aposta com um amigo que trabalhava com apostas esportivas de que eu conseguiria acertar o spread em 50% ou mais de todos os jogos da temporada regular da NFL. Se eu ganhar, levo US$ 1.000. Se ele ganhar, pago US$ 500. Até domingo, 31/10/2010, eu estava com 19 vitórias e ele está falando em fazer um acordo. Qual seria uma boa oferta para aceitar?
Aposta sensacional, é como tirar doce de criança. É como ganhar 2 para 1 no cara ou coroa. Melhor ainda, já que você ganharia mesmo em caso de empate.
No momento em que este texto foi escrito, 95 jogos foram disputados dos 256 previstos para a temporada regular. Utilizando a distribuição binomial, demonstro que sua probabilidade de vitória é de 99,87%. Um valor justo para o acordo seria de US$ 998,02.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Uma casa de apostas em Las Vegas divulgou um total obviamente incorreto para um jogo de futebol americano universitário. O número de pontos anunciado era 43, mas eles ofereceram 53. Então, apostei no "menos de" umas 20 vezes, com valores pequenos, para não chamar atenção nem alterar a linha. Como esperado, ganhei. Agora estou nervoso para apresentar as apostas para pagamento. Os cassinos teriam justificativa para se recusar a pagar?
Eu apostaria 10 para 1 que você receberá o pagamento, embora eles possam ter algumas palavras com você antes. O motivo da minha dúvida é que uma casa de apostas pode cancelar uma aposta que foi obviamente feita por engano, com a permissão do Conselho de Controle de Jogos.
"Uma casa de apostas não pode rescindir unilateralmente qualquer aposta sem a prévia aprovação por escrito do presidente." -- Regulamento de Nevada 22.115
Embora esse direito exista, com base em relatos, ele raramente é invocado. Me avise o que acontecer.
P.S.: Mais tarde, a pessoa que fez a pergunta me informou que o pagamento foi efetuado sem maiores problemas.
Existe uma aposta no Super Bowl sobre o número de pontos no Scrabble que compõem o sobrenome do primeiro jogador a marcar um touchdown. A linha de aposta é de 10½ e -115 tanto para o "mais" quanto para o "menos". Alguma das opções é uma boa aposta?
Gosto de apostas criativas como esta. Elas podem ser encontradas nos cassinos Boyd, assim como no Palms, El Cortez e South Point. Para responder à pergunta, analisei outro conjunto de apostas no jogador específico que marcará o primeiro touchdown. Essas probabilidades são mostradas na segunda coluna da tabela abaixo. Para simplificar, estou ignorando a aposta em todos os jogadores com odds de 5-1 e a aposta em nenhum touchdown com odds de 100-1. Em seguida, converti essas vitórias para a “probabilidade justa” na terceira coluna, ou seja, a probabilidade de vitória necessária para que a aposta seja exatamente justa. Essas probabilidades estão inflacionadas, devido à redução do valor pago por cada vitória, razão pela qual a soma é de 166%. A “probabilidade ajustada” na quarta coluna mostra as probabilidades justas divididas por 1,660842, de modo que a probabilidade total seja de 100%. A quinta coluna mostra o número de pontos de Scrabble no nome de cada jogador. Os “pontos de Scrabble esperados” na sexta coluna são o produto da probabilidade pelos pontos de Scrabble. A célula inferior direita mostra que a média de pontos de Scrabble é de 14,18521.
Considerando a média, a aposta no "mais de" parece ser a mais adequada. Analisando jogador por jogador, a probabilidade de 11 ou mais pontos no Scrabble é de 0,641894, o que corresponde a uma linha justa de -179. Portanto, apostar no "mais de" a -115 é uma excelente opção. Apostando contra 115, o jogador tem uma vantagem de 20% no "mais de".
Infelizmente, quando fui apostar, a cotação já havia subido para -180.
Pontos do Scrabble para o primeiro jogador a marcar um touchdown no Super Bowl
| Nome | Probabilidades divulgadas | Probabilidade justa | Probabilidade Ajustada | Total de pontos no Scrabble | Pontuação esperada no Scrabble |
|---|---|---|---|---|---|
| Mendenhall | 4 | 0,200000 | 0,120421 | 20 | 2,408416 |
| Jennings | 4.5 | 0,181818 | 0,109473 | 22 | 2,408416 |
| Starks | 5 | 0,166667 | 0,100351 | 10 | 1,003507 |
| Wallace | 7 | 0,125000 | 0,075263 | 15 | 1,128945 |
| Ala | 8 | 0,111111 | 0,066900 | 8 | 0,535204 |
| Rodgers | 8 | 0,111111 | 0,066900 | 10 | 0,669005 |
| Nelson | 8 | 0,111111 | 0,066900 | 9 | 0,602104 |
| Moleiro | 10 | 0,090909 | 0,054737 | 11 | 0,602104 |
| Motorista | 10 | 0,090909 | 0,054737 | 11 | 0,602104 |
| Jones | 12 | 0,076923 | 0,046316 | 15 | 0,694735 |
| Roethlisberger | 12 | 0,076923 | 0,046316 | 22 | 1,018945 |
| Sanders | 15 | 0,062500 | 0,037632 | 9 | 0,338684 |
| Marrom | 18 | 0,052632 | 0,031690 | 12 | 0,380276 |
| Homem vermelho | 18 | 0,052632 | 0,031690 | 11 | 0,348587 |
| Quarless | 20 | 0,047619 | 0,028672 | 19 | 0,544761 |
| Kuhn | 25 | 0,038462 | 0,023158 | 12 | 0,277894 |
| Jackson | 30 | 0,032258 | 0,019423 | 24 | 0,466145 |
| Moore | 30 | 0,032258 | 0,019423 | 8 | 0,155382 |
| Totais | 1,660842 | 1.000000 | 14.185214 | ||
Infelizmente, quando voltei ao cassino para apostar, a cotação já havia subido para -180.
PS: Horas antes do jogo, fiz uma aposta com odds de -170. Infelizmente, perdi. O primeiro jogador a marcar um touchdown foi Jordy Nelson. Nelson tem 9 pontos no Scrabble.
Como se saíram os azarões contra o spread durante a temporada 2010-2011 da NFL?
Nos 267 jogos disputados, o favorito venceu o spread 128 vezes, o azarão venceu 133 vezes e 6 jogos terminaram em empate. Das apostas resolvidas, o azarão venceu 51%.
O que é mais interessante são as apostas em "mais" e "menos". A aposta "mais" venceu 148 vezes, a "menos" 114 vezes e houve 5 empates. Das apostas resolvidas, a "mais" venceu 56,5% das vezes. A probabilidade de a "menos" vencer 114 jogos ou menos em 262 jogos resolvidos é de 2,1%.
No jogo entre Rams e Cardinals de 6 de novembro de 2011, os Rams marcaram dois safeties no terceiro quarto. Qual a probabilidade disso acontecer?
A probabilidade de pelo menos um safety por jogo é de 5,77%, com base na experiência histórica.
O número esperado de safeties por jogo seria -ln(1-0,0577) = 0,0594.
O número esperado por trimestre por equipe seria de 0,0594/8 = 0,0074.
A probabilidade de exatamente dois safeties da mesma equipe em um único quarto seria e -0,0074 ×0,0074 2 /fact(2) = 1 em 36.505.
Em uma temporada da NFL, há 267 jogos e 267 × 8 = 2.136 quartos de equipe. Portanto, de acordo com minha estimativa, isso ocorrerá em média uma vez a cada 36.505/2.136 = 17,1 anos.
Isso deve ser considerado apenas um palpite aproximado. Existem fatores no jogo que não estou levando em conta, em prol da simplicidade.
Você já ouviu a história da Princesa, a camela do zoológico Popcorn Park em Nova Jersey, que tem um histórico de 88 vitórias e 51 derrotas em apostas contra o spread na NFL? Quais são as chances disso?
Sem contar os empates, a probabilidade de acertar pelo menos 88 palpites em 139 tentativas é de 0,00107355, ou 1 em 931. Isso é bem decepcionante. Tenho certeza de que existem outros 930 animais por aí que se saíram pior e sobre os quais ninguém escreve. Para mais informações sobre a Princesa, leia o artigo " Camelo de Nova Jersey prevê vitória dos Giants sobre os Patriots" no ESPN.com.
Obrigado pela nova seção sobre cartões de apostas múltiplas . Usei suas dicas e consegui estas linhas (o spread de pontos do mercado está entre parênteses):
- Contas +3,5 (+3)
- Carregadores +7,5 (+7)
- Cardinals -2,5 (-3)
- Golfinhos -2,5 (-3)
- Ursos +2,5 (0)
Qual é a minha vantagem nesta aposta?
Vou assumir que as probabilidades são de 25 para 1, que está disponível no cartão de meio ponto das casas de apostas esportivas Golden Nugget, South Point e William Hill.
A tabela abaixo mostra a linha que você obteve e a linha do preço de mercado.
Primeiro, a probabilidade de um azarão vencer a aposta é de 51,6%. Isso equivale a uma linha justa de -106,6 para o azarão. Portanto, você está ganhando 6,6 pontos-base com os azarões e perdendo-os com os favoritos.
Em segundo lugar, minha tabela sobre a compra de meio ponto na NFL mostra o preço justo a pagar por cada meio ponto extra. Por exemplo, obter o meio ponto extra com um handicap de 3 vale a pena apostar -121,4, ou 21,4 pontos base.
A tabela detalha quantos pontos-base você está recebendo. Para os Bears, dobrei os pontos-base para 1 e 2, já que você transforma uma derrota em vitória se cruzar esses números.
A tabela converte então o total de pontos base em uma probabilidade de vitória. A fórmula é p = (100+b)/(200+b), onde p = probabilidade de vitória e b = número de pontos base.
A última linha mostra o produto de cada aposta vencedora, resultando em uma probabilidade de acerto na aposta combinada de 0,046751. Com odds de 25 para 1, essa aposta tem um retorno esperado de 0,046751 * 25 - 1 = 0,168783. Em outras palavras, uma vantagem de 16,9%. Muito bem!
Cartão Rudeboyoi Parlay
| Equipe | Parlay Cartão | Justo | azarão Base Pontos | Total Extra Pontos | Total | Probabilidade |
|---|---|---|---|---|---|---|
| Contas | 3,5 | 3 | 6.6 | 20,8 | 27,4 | 0,560246 |
| Carregadores | 7,5 | 7 | 6.6 | 11.9 | 18,5 | 0,542334 |
| Cardeais | -2,5 | -3 | -6,6 | 20,8 | 14.2 | 0,533147 |
| Golfinhos | -2,5 | -3 | -6,6 | 20,8 | 14.2 | 0,533147 |
| Ursos | 2,5 | 0 | 0 | 18.0 | 18.0 | 0,541321 |
| Produto | 0,046751 | |||||
Você ouviu falar da concessionária de carros em Seattle que teve que pagar US$ 420.000 porque o Seahawks venceu o Giants sem marcar pontos? Li que eles tiveram que pagar US$ 7.000 pelo seguro contra esse tipo de prejuízo. Qual seria um valor justo de seguro?
De acordo com o artigo " Concessionária de carros de Washington paga US$ 420.000 após derrota dos Seahawks por shutout" , a concessionária realizou uma promoção para pagar US$ 35.000 a doze vencedores caso os Seahawks vencessem os Giants por shutout na partida da semana 15, realizada em 15 de dezembro de 2013. O artigo afirma ainda que a concessionária pagou US$ 7.000 por uma apólice de seguro para cobrir o pagamento caso isso de fato ocorresse.
Com base em todos os jogos da NFL das temporadas de 1983 a 2012, um lado específico de cada partida não marcou pontos. No entanto, como azarão por sete pontos, em um jogo com uma previsão de pontos acima da média, eu diria que a probabilidade dos Giants não marcarem pontos era maior do que a média. A previsão de pontos para aquele jogo era de 41. Vamos fazer um pouco de álgebra para calcular o número esperado de pontos dos Giants.
Deixar:
s = Pontos dos Seahawks
g = Pontos dos Giants
Sabemos que s+g=41 e s=g+7, com base na diferença de pontos e no total de pontos (acima/abaixo).
Substituindo a segunda equação na primeira:
(g+7) + g = 41
2g + 7 = 41
2g = 34
g = 17
Em seguida, vamos analisar a probabilidade de um shutout com base no número estimado de pontos de cada equipe, considerando as temporadas de 1983 a 2012. Ignorei as linhas em que o tamanho da amostra era zero.
Probabilidade de não marcar gols
| Estimado Pontos | Tamanho da amostra | Desligamentos | Razão |
|---|---|---|---|
| 5,25 | 1 | 0 | 0,0% |
| 6,50 | 1 | 0 | 0,0% |
| 7,75 | 1 | 0 | 0,0% |
| 8,00 | 1 | 0 | 0,0% |
| 8,25 | 3 | 0 | 0,0% |
| 8,50 | 2 | 0 | 0,0% |
| 8,75 | 2 | 0 | 0,0% |
| 9,00 | 2 | 0 | 0,0% |
| 9,50 | 4 | 0 | 0,0% |
| 9,75 | 6 | 1 | 16,7% |
| 10,00 | 10 | 1 | 10,0% |
| 10,25 | 7 | 0 | 0,0% |
| 10,50 | 14 | 2 | 14,3% |
| 10,75 | 7 | 1 | 14,3% |
| 11:00 | 13 | 1 | 7,7% |
| 11,25 | 21 | 1 | 4,8% |
| 11,50 | 22 | 3 | 13,6% |
| 11,75 | 23 | 1 | 4,3% |
| 12h00 | 34 | 2 | 5,9% |
| 12,25 | 36 | 7 | 19,4% |
| 12,50 | 41 | 3 | 7,3% |
| 12,75 | 39 | 4 | 10,3% |
| 13:00 | 55 | 1 | 1,8% |
| 13,25 | 58 | 5 | 8,6% |
| 13,50 | 78 | 1 | 1,3% |
| 13,75 | 89 | 5 | 5,6% |
| 14:00 | 92 | 4 | 4,3% |
| 14,25 | 108 | 7 | 6,5% |
| 14,50 | 117 | 8 | 6,8% |
| 14,75 | 141 | 7 | 5,0% |
| 15h00 | 160 | 7 | 4,4% |
| 15,25 | 160 | 7 | 4,4% |
| 15,50 | 213 | 7 | 3,3% |
| 15,75 | 198 | 11 | 5,6% |
| 16:00 | 206 | 6 | 2,9% |
| 16,25 | 221 | 12 | 5,4% |
| 16,50 | 241 | 10 | 4,1% |
| 16,75 | 273 | 7 | 2,6% |
| 17:00 | 306 | 8 | 2,6% |
| 17,25 | 305 | 8 | 2,6% |
| 17,50 | 306 | 10 | 3,3% |
| 17,75 | 323 | 4 | 1,2% |
| 18h00 | 299 | 8 | 2,7% |
| 18,25 | 332 | 8 | 2,4% |
| 18,50 | 309 | 9 | 2,9% |
| 18.75 | 307 | 7 | 2,3% |
| 19h00 | 356 | 8 | 2,2% |
| 19,25 | 389 | 5 | 1,3% |
| 19,50 | 361 | 5 | 1,4% |
| 19,75 | 343 | 6 | 1,7% |
| 20,00 | 402 | 8 | 2,0% |
| 20,25 | 379 | 6 | 1,6% |
| 20,50 | 359 | 3 | 0,8% |
| 20,75 | 353 | 5 | 1,4% |
| 21h00 | 344 | 1 | 0,3% |
| 21,25 | 317 | 3 | 0,9% |
| 21,50 | 341 | 2 | 0,6% |
| 21,75 | 331 | 1 | 0,3% |
| 22h00 | 369 | 1 | 0,3% |
| 22,25 | 336 | 0 | 0,0% |
| 22,50 | 316 | 2 | 0,6% |
| 22,75 | 280 | 3 | 1,1% |
| 23h00 | 311 | 1 | 0,3% |
| 23,25 | 290 | 3 | 1,0% |
| 23,50 | 279 | 1 | 0,4% |
| 23,75 | 255 | 1 | 0,4% |
| 24,00 | 246 | 1 | 0,4% |
| 24,25 | 219 | 0 | 0,0% |
| 24,50 | 230 | 2 | 0,9% |
| 24,75 | 230 | 1 | 0,4% |
| 25,00 | 212 | 2 | 0,9% |
| 25,25 | 207 | 0 | 0,0% |
| 25,50 | 176 | 1 | 0,6% |
| 25,75 | 154 | 0 | 0,0% |
| 26,00 | 154 | 1 | 0,6% |
| 26,25 | 113 | 0 | 0,0% |
| 26,50 | 137 | 0 | 0,0% |
| 26,75 | 122 | 0 | 0,0% |
| 27,00 | 95 | 0 | 0,0% |
| 27,25 | 98 | 0 | 0,0% |
| 27,50 | 83 | 0 | 0,0% |
| 27,75 | 81 | 0 | 0,0% |
| 28,00 | 82 | 0 | 0,0% |
| 28,25 | 55 | 1 | 1,8% |
| 28,50 | 56 | 0 | 0,0% |
| 28,75 | 51 | 0 | 0,0% |
| 29,00 | 48 | 0 | 0,0% |
| 29,25 | 34 | 0 | 0,0% |
| 29,50 | 24 | 0 | 0,0% |
| 29,75 | 25 | 0 | 0,0% |
| 30,00 | 24 | 0 | 0,0% |
| 30,25 | 21 | 0 | 0,0% |
| 30,50 | 18 | 0 | 0,0% |
| 30,75 | 23 | 0 | 0,0% |
| 31,00 | 16 | 0 | 0,0% |
| 31,25 | 15 | 0 | 0,0% |
| 31,50 | 8 | 0 | 0,0% |
| 31,75 | 3 | 0 | 0,0% |
| 32,00 | 6 | 0 | 0,0% |
| 32,25 | 7 | 0 | 0,0% |
| 32,50 | 6 | 0 | 0,0% |
| 32,75 | 3 | 0 | 0,0% |
| 33,00 | 4 | 0 | 0,0% |
| 33,25 | 6 | 0 | 0,0% |
| 33,50 | 5 | 0 | 0,0% |
| 34,75 | 4 | 0 | 0,0% |
| 35,00 | 2 | 0 | 0,0% |
| 35,50 | 1 | 0 | 0,0% |
| 36,00 | 2 | 0 | 0,0% |
| 36,25 | 1 | 0 | 0,0% |
| 36,50 | 1 | 0 | 0,0% |
| 37,25 | 1 | 0 | 0,0% |
| 37,75 | 2 | 0 | 0,0% |
| 42,25 | 1 | 0 | 0,0% |
Os próximos passos são muito complexos para explicar aqui, mas desenvolvi uma fórmula para a probabilidade de um shutout, dado o número estimado de pontos.
p = Pontos estimados.
x = 1,562545 - 0,302485 * p
probabilidade de shutout = e x /(1+e x )
O gráfico a seguir mostra a probabilidade real e estimada de uma partida sem sofrer gols por uma diferença de 14 a 22 pontos.
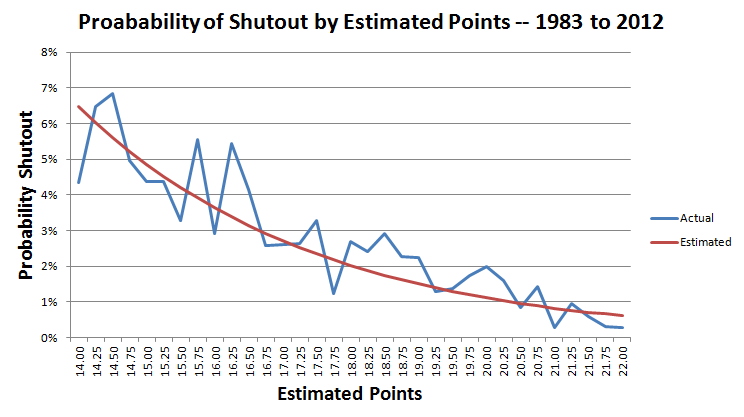
Na partida em questão, esperava-se que os Giants marcassem 17 pontos.
Utilizando a fórmula acima da tabela:
x = 1,562545 -0,302485 * 17 = -3,579706
Probabilidade de shutout = exp(-3,579706)/( exp(-3,579706)+1) = 2,71%. Para ser exato, 0,0271275.
Considerando que a concessionária teria que pagar US$ 420.000 caso o Giants perdesse por 4 a 0, o custo justo do seguro seria de US$ 420.000 × 0,0271275 = US$ 11.394. Normalmente, as seguradoras que oferecem promoções incomuns como essa dobram o custo justo, então eu esperaria um prêmio de US$ 22.788. Portanto, o prêmio de US$ 7.000 pago pela concessionária foi uma pechincha. Supondo que o chefe revise os cálculos, eu não gostaria de estar no lugar de quem calculou esse prêmio de US$ 7.000.
Essa questão foi levantada e discutida no meu fórum no Wizard of Vegas .
Quem oferece as melhores probabilidades para apostas futuras em Las Vegas?
De acordo com as apostas futuras no Super Bowl de 2015, esta é a vantagem média da casa em vários grupos de apostas esportivas de Las Vegas.
Vantagem da casa em futuros esportivos
| Apostas Esportivas | Borda da casa |
|---|---|
| Tecnologia CG | 21,90% |
| William Hill | 26,63% |
| Wynn | 27,96% |
| Césares | 35,49% |
| Estações/El Cortez | 38,33% |
| Pepita de Ouro | 39,75% |
| MGM | 40,88% |
| Boyd/Costa | 49,35% |
| TI | 57,93% |
Para calcular a vantagem média da casa em qualquer conjunto de apostas futuras, utilize minha Calculadora de Apostas Futuras Esportivas .
Ouvi dizer que o Jerry's Nugget não oferece mais as odds atraentes para os teasers da NFL. Isso é verdade?
Infelizmente, sim. O Jerry's Nugget foi o último lugar a oferecer odds generosas de -110 para um teaser de 2 jogos com 6 pontos de vantagem na NFL, +180 para três jogos e +300 para quatro jogos. Ao fazer teasers Wong (cruzando as margens de vitória de 3 e 7 pontos), essa era uma aposta com vantagem sólida.
Você pode encontrar todas as probabilidades atuais de apostas combinadas e teasers em Las Vegas na minha pesquisa de casas de apostas esportivas no Wizard of Vegas.com.
Para mais informações sobre teasers de futebol americano em geral, consulte minha página sobre Apostas Teaser na NFL .
Na NFL, é uma boa aposta apostar em mais de 50 pontos em uma casa de apostas e menos de 52,5 em outra?
Você pode usar meus totais alternativos na NFL para esse tipo de pergunta. Isso mostrará a probabilidade e a linha justa para obter pontos extras em uma aposta no total.
Vamos supor que a linha justa de over/under seja 51. A primeira tabela mostra que a probabilidade de ganhar apostando em menos de 52,5 é de 54,4%, assumindo que não haja empate. A terceira tabela mostra que a probabilidade de ganhar apostando em mais de 52,5 é de 53,5%.
Para vencer a taxa de 10%, você precisa ter uma probabilidade de ganhar de 11/21 = 52,38%. A média dessas duas apostas é de 53,95%, então, sim, jogue na aposta do meio. Sua vantagem é de 3,0%.
Enquanto escrevo esta pergunta, logo após o término da temporada regular da NFL, a Bovada está oferecendo odds de 18 para 1 para o Carolina Panthers vencer o campeonato da NFC. Eles já são favoritos por seis pontos para vencer o primeiro jogo contra o Arizona. Faltam apenas mais dois jogos depois disso.
Você não acha que eu poderia garantir uma vitória apostando na vitória do Carolina no NFC e, ao longo do caminho, apostando no vencedor, independentemente de quem eles enfrentarem?
Não! Apostas futuras e apostas no favorito na linha de dinheiro são duas das piores apostas que você pode fazer em futebol. Isso soa como um sistema de apostas, somando uma sequência de apostas negativas e esperando que o resultado final seja positivo. No entanto, provavelmente precisarei de mais do que isso para te convencer, então vamos analisar os números.
Primeiramente, os Panthers só estão nos playoffs porque são o time menos ruim em uma divisão péssima (a NFC Sul). Seu recorde é de 7 vitórias e 8 derrotas, e eles sofreram 35 pontos a mais do que marcaram em toda a temporada.
Se eles são tão ruins, por que são favoritos por seis pontos contra o Arizona Cardinals, você pode se perguntar? O Arizona chegou aos playoffs principalmente graças aos esforços de Carson Palmer nos primeiros seis jogos. Ele se machucou no sexto jogo, mas mesmo assim eles conseguiram se classificar para os playoffs. Além disso, o Carolina tem a vantagem de jogar em casa.
Considerando que Carolina é favorita por seis pontos contra o Arizona, mostro que a probabilidade de vitória dessa partida é de 70,3%.
Supondo que vençam, provavelmente precisarão derrotar Green Bay e Seattle para conquistar o título da NFC. Quais são as chances de vencer essas duas equipes? Lembre-se que, pelas regras dos playoffs , eles serão os visitantes nas duas partidas.
Existe uma maneira fácil de obter uma estimativa precisa da diferença de pontos em qualquer jogo. Aqui está minha fórmula Wizard para calcular a diferença de pontos para o time da casa:
(Pontos líquidos por jogo da equipe visitante) - (Pontos líquidos por jogo da equipe mandante) - 2,67.
Vamos analisar um confronto hipotético entre Arizona e Green Bay.
Durante a temporada de 2014, o Carolina Panthers teve um saldo de pontos negativo de -35. Já o Green Bay Packers teve um saldo positivo de +138. Dividindo ambos os números por 16, já que a temporada tem 16 jogos, obtemos uma margem média de vitória por jogo de:
Carolina: -2,1875
Green Bay: +8.6250
Usando minha fórmula, o time da casa, Green Bay, deveria ter um spread de -2,1875 - 8,6250 - 2,67 = -13,4825.
Portanto, Green Bay seria o favorito por cerca de 13,5 pontos contra Carolina. Vou pular os cálculos nesta etapa, mas mostro que a probabilidade de Carolina vencer como azarão por 13,5 pontos é de 14,3%.
Seattle tem um desempenho quase tão bom quanto o de Green Bay, com 140 pontos líquidos na temporada. Portanto, Carolina também teria cerca de 14,3% de chance de vencer essa partida.
A probabilidade de Carolina vencer os três jogos é de 70,3% × 14,3% × 14,3% = 1,44%. Portanto, uma aposta futura justa com essa probabilidade é de 68,6 para 1!
Sim, você poderia argumentar que Detroit ou Dallas poderiam ter sorte e chegar à final da conferência. Você também poderia argumentar que as chances de Carolina vencer Green Bay e Seattle são positivamente correlacionadas. No entanto, essas são considerações menores diante do fato de que minha linha de aposta aproximada é de 68,6 e você está recebendo apenas 18.
Você também precisa considerar o custo de apostar nos favoritos na linha de dinheiro. Geralmente, essa é uma aposta ruim. Apostadores conservadores adoram apostar em grandes favoritos na linha de dinheiro, criando valor na direção oposta. É uma aposta razoavelmente justa apostar em azarões com sete pontos ou mais de vantagem na linha de dinheiro, o que significa que os apostadores nos favoritos estão pagando toda a comissão.
Vamos ser generosos e supor que você consiga odds de +250 para o Arizona e aposte 5 para 1 nos dois jogos seguintes. Digamos também que você aposte US$ 100 no Carolina com odds de 18 para 1.
Primeiro, você aposta $40 no Arizona com odds de +250 como proteção. Se eles ganharem, você ganha $100 nessa aposta e perde $100 na aposta futura, ficando no zero a zero.
Se Carolina vencer o Arizona, você aposta US$ 700 para ganhar US$ 140 com Seattle. Se Seattle vencer, o que deve acontecer, você terá um lucro de US$ 140, o que compensará suas perdas com o Arizona e a aposta futura, deixando você no zero a zero.
Se Carolina vencer Carolina, você terá que apostar US$ 4.200 para recuperar os US$ 840 perdidos nas apostas em Arizona, Seattle e na aposta futura. Se Carolina perder, você não terá prejuízo. Se vencer, você perderá US$ 40 + US$ 700 + US$ 4.200 = US$ 4.940. Os US$ 1.800 que você ganhará na aposta futura não serão suficientes para recuperar esse valor.
Em resumo, sua ideia de apostar na vitória do Carolina na NFC e fazer apostas de cobertura ao longo do caminho é altamente imprudente.
Qual é o seu conselho para piscinas de suicídio?
Para quem não sabe, um bolão suicida é uma competição em que o último a ficar de pé vence, geralmente baseada na NFL, embora qualquer liga esportiva sirva. Aqui estão as regras básicas.
- Todos os jogadores pagam o mesmo valor para jogar.
- Toda semana, cada jogador deve prever o vencedor de uma partida. Todos os jogos são pontuados sem considerar o spread.
- Se um jogador errar alguma vez, ele é imediatamente eliminado da competição.
- Nenhum jogador pode escolher a mesma equipe mais de uma vez.
- O último jogador que permanecer em pé ganha o pote.
Poderão existir regras adicionais, como a pessoa que organiza o jogo receber uma parte do prémio e a divisão do prémio quando restarem poucas pessoas, apenas se houver acordo mútuo.
Antes de prosseguirmos, aqui estão os resultados da última temporada, retirados do site officefootballpool.com .
Bolão de Futebol do Escritório — Temporada de 2014
| Semana | Equipe | Espalhar | Escolhas |
|---|---|---|---|
| 1 | Phil | -10,5 | 54 |
| 1 | Chique | -7 | 29 |
| 1 | Poço | -6,5 | 14 |
| 1 | Det | -6 | 6 |
| 1 | KC | -3 | 5 |
| 1 | NYJ | -5,5 | 5 |
| 1 | NE | -4 | 1 |
| 1 | São Francisco | -4,5 | 1 |
| 1 | StL | -3,5 | 1 |
| 2 | Covil | -12,5 | 38 |
| 2 | GB | -8 | 23 |
| 2 | NÃO | -6,5 | 7 |
| 2 | São Francisco | -7 | 5 |
| 2 | TB | -5,5 | 3 |
| 2 | Lavar | -6 | 2 |
| 2 | Cin | -5,5 | 1 |
| 2 | NE | -5,5 | 1 |
| 3 | NE | -14 | 44 |
| 3 | NÃO | -10 | 16 |
| 3 | Atl | -6,5 | 3 |
| 3 | Cin | -6,5 | 1 |
| 3 | Índia | -6 | 1 |
| 4 | SD | -13 | 34 |
| 4 | Índia | -7,5 | 20 |
| 4 | Poço | -7,5 | 10 |
| 4 | Bal | -3 | 1 |
| 5 | NÃO | -10 | 21 |
| 5 | GB | -8 | 13 |
| 5 | Covil | -7,5 | 6 |
| 5 | Det | -6,5 | 5 |
| 5 | Phil | -6,5 | 3 |
| 5 | Dal | -6,5 | 2 |
| 5 | Poço | -6 | 2 |
| 5 | SD | -6,5 | 1 |
| 5 | Mar | -7 | 1 |
| 5 | São Francisco | -5 | 1 |
| 6 | Mar | -8,5 | 21 |
| 6 | Covil | -9,5 | 13 |
| 6 | SD | -7 | 7 |
| 6 | Cin | -6,5 | 5 |
| 6 | Dez | -4 | 2 |
| 6 | Atl | -3 | 1 |
| 6 | São Francisco | -3 | 1 |
| 7 | NE | -9,5 | 9 |
| 7 | Mar | -6,5 | 9 |
| 7 | GB | -6,5 | 3 |
| 7 | Bal | -6,5 | 2 |
| 7 | Buf | -5,5 | 2 |
| 7 | Lavar | -5 | 2 |
| 7 | Dal | -6,5 | 1 |
| 8 | Dal | -9,5 | 12 |
| 8 | KC | -7 | 5 |
| 8 | Clev | -7 | 1 |
| 8 | Mia | -6 | 1 |
| 9 | São Francisco | -10 | 3 |
| 9 | Cin | -10.5 | 2 |
| 9 | Mar | -14,5 | 2 |
| 10 | Bal | -9,5 | 2 |
| 10 | Cin | -6 | 1 |
| 10 | Mar | -9 | 1 |
| 11 | GB | -5,5 | 1 |
| 11 | Meu | -6 | 1 |
| 11 | NÃO | -7 | 1 |
| 12 | Índia | -14 | 2 |
| 13 | Bal | -6,5 | 1 |
| 13 | Det | -7 | 1 |
| 14 | NÃO | -10 | 1 |
A coluna "escolhas" refere-se ao número de jogadores que escolheram aquela equipe.
Note que em nenhum momento alguém escolheu o azarão. Nas 497 apostas feitas, a diferença média de pontos foi de 9,3.
Não sei por que registraram uma escolha na semana 14, já que só restava um jogador naquele momento.
Com base neste estudo do comportamento de outros jogadores, aqui está minha estratégia básica para bolões suicidas. Estas são apenas diretrizes gerais e não regras rígidas que você deve seguir todas as semanas.
- Lembre-se de que seu inimigo são os outros jogadores. Não se concentre muito em analisar os resultados da NFL, mas sim em vencer seus adversários.
- Não escolha o grande favorito. É isso que a maioria das pessoas fará. Com sorte, esse grande favorito perderá e o número de competidores diminuirá significativamente. Você quer ser um sobrevivente, e não uma vítima, quando um grande favorito perde.
- Não se esqueça da regra de que você não pode escolher o mesmo time duas vezes. Dito isso, nem sempre você pode escolher times excelentes. Às vezes, você deve escolher times medianos jogando contra times ruins, para preservar as vitórias fáceis dos melhores times.
- Não se preocupe em analisar as probabilidades. Use apenas a diferença de pontos como um indicador das suas chances de ganhar em qualquer palpite.
- Se uma semana tiver exatamente dois grandes favoritos, eu evitaria ambos. Lembre-se de que você está tentando equilibrar a escolha de jogos com alta probabilidade de vitória, sem seguir a maioria. Como regra geral, acho que escolher o terceiro time com maior handicap é uma boa ideia, especialmente se você não estiver desperdiçando uma das melhores equipes.
Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .
Qual a sua opinião sobre como as novas regras para o ponto após um touchdown afetarão as apostas múltiplas de meio ponto ?
Para benefício de outros leitores, um dos meus truques é aproveitar os meio pontos extras em apostas combinadas de 3 e 7 pontos. Já demonstrei que essa é uma jogada vantajosa confiável, embora muito volátil.
A nova regra recua o chute extra para a linha de 15 jardas. Isso deve diminuir a probabilidade de sucesso do chute e induzir mais tentativas de conversão de dois pontos. Com mais tentativas de conversão de dois pontos, sejam elas bem-sucedidas ou não, não deve haver tantos jogos decididos por três ou sete pontos, diminuindo assim o valor de obter o meio ponto extra nesses números-chave em apostas múltiplas de meio ponto. Devemos nos preocupar? Vamos ver.
Em primeiro lugar, devemos nos preocupar, mas não necessariamente por este motivo. Outras mudanças nas regras prejudicaram a agressividade da defesa, levando a jogos com placares mais altos. O gráfico a seguir mostra a média de pontos marcados por jogo em cada temporada, de 1994 a 2014.
Como mostra o gráfico, a média de pontos por jogo manteve-se próxima de 42 até 2006. No entanto, a partir de 2007, a média vem aumentando em cerca de meio ponto por ano. Isso levanta a questão de se esse aumento na pontuação média tende a achatar a distribuição da margem de vitória, especialmente para os números mágicos de 3 e 7. O próximo gráfico mostra a probabilidade de uma margem de vitória de três e sete pontos por ano.
Como você pode ver, a probabilidade de uma vitória por sete pontos se mantém estável em 9,1%. No entanto, a probabilidade de uma vitória por três pontos vem diminuindo constantemente, especialmente desde 2004. Isso é ruim porque há muitas partidas com diferença de três pontos na NFL.
Independentemente da causa da diminuição das margens de vitória por três pontos, o valor das apostas combinadas de meio ponto está caindo. Será que a situação vai piorar ainda mais com a nova regra do ponto extra?
Minha resposta é que deveria doer, mas não muito. Antes da mudança na regra, calculo que cerca de 4,8% dos touchdowns eram seguidos por uma tentativa de conversão de dois pontos. Enquanto escrevo isto, ocorreram apenas duas semanas de jogos desde a mudança na regra. Nas duas primeiras semanas da temporada de 2015, houve 167 touchdowns e 15 foram seguidos por uma tentativa de conversão de dois pontos, resultando em uma taxa de tentativas de 9,0%.
Matematicamente falando, acho que tentar a conversão de dois pontos deveria ser muito mais comum, especialmente para times mais fracos que buscam variar o jogo, e não entendo por que não é. Não foi isso que você perguntou, mas eu precisava desabafar.
Digamos, por exemplo, que eu consiga acertar 54% das apostas contra o spread consistentemente. Para aumentar meu saldo o mais rápido possível, qual seria a opção mais lucrativa: apostar em acumuladas de três jogos com odds de 6 para 1?
Boa pergunta. Sua vantagem ao apostar contra 11 para 10 é de 3,09%, enquanto na aposta combinada é de 10,22%. Isso parece ser um ótimo argumento a favor da aposta combinada.
No entanto, lembre-se de que a estratégia ideal para aumentar a banca em qualquer jogo com vantagem é usar o Critério de Kelly . De acordo com Kelly, o tamanho ideal da aposta é aquele que maximiza o logaritmo esperado da banca após a aposta. Para apostas com apenas dois resultados possíveis, o tamanho ideal da aposta é, convenientemente, a vantagem dividida pelo pagamento da aposta em uma proporção de "um para um".
As apostas simples pagam de 10 a 11. Isso tornaria o tamanho ideal da aposta 0,030909/(10/11) = 0,034000. Com uma vantagem do jogador de 3,09%, você pode esperar ganhar 0,001051 vezes o seu saldo por jogo em apostas simples.
O tamanho ideal da aposta combinada é 0,102248/6 = 0,017041. Com uma vantagem do jogador de 0,102248, você pode esperar ganhar 0,001742 vezes o seu saldo por jogo apostando diretamente.
No entanto, as apostas simples são melhores porque permitem apostar três vezes. Portanto, multiplique o ganho esperado por aposta simples por três para obter 3 × 0,001051 = 0,003153. Isso representa um aumento de 81% em relação ao crescimento da banca em apostas múltiplas.
Se você tem um saldo tão grande que chega a atingir os limites máximos de apostas, provavelmente é melhor fazer primeiro uma aposta combinada, que geralmente não altera as linhas, e depois fazer suas apostas simples.
Essa questão é levantada e discutida no meu fórum no Wizard of Vegas .
Como você sabe, o ponto extra agora deve ser tentado da linha de 15 jardas na NFL, enquanto a tentativa de conversão de dois pontos permanece na linha de duas jardas. Você acha que isso muda o cálculo da decisão? Em outras palavras, qual é a jogada correta agora?
É uma decisão controversa, que acredito ser o objetivo da NFL ao alterar a regra. Alguns fatores a serem considerados na tomada de decisão são:
- Probabilidade de sucesso ao chutar.
- Probabilidade de sucesso ao tentar a conversão de dois pontos.
- Probabilidades gerais de vitória de cada equipe.
No final do jogo, também é crucial considerar os números-chave. Por exemplo, se estiver bem perto do fim e você acabou de marcar um touchdown, colocando seu time três pontos à frente, então você deve chutar. Se acertar, você estará quatro pontos à frente e forçará o outro time a marcar um touchdown para vencer. Se tentar a conversão de dois pontos e errar, o outro time pode empatar com apenas um field goal. Portanto, vou limitar minha discussão ao início do jogo, quando os números-chave não são um fator tão importante.
Para responder à sua pergunta, escrevi um programa de simulação. Embora seja um tanto rudimentar, acredito que ele reflita com bastante precisão a natureza da NFL em termos de field goals, touchdowns e turnovers.
De acordo com o artigo " Qual o efeito de mover os pontos extras para a linha de 15 jardas?" de Kevin Rudy, a probabilidade de converter o ponto extra a partir da linha de 15 jardas é de 94,2%. Inseri 94% no meu programa para manter os números arredondados.
Existe mais divergência quanto à probabilidade de conversão de dois pontos. Parece óbvio que isso também varia significativamente de acordo com a defesa e o ataque específicos. O que eu fiz foi executar simulações com taxas de sucesso de conversão de dois pontos entre 46% e 50%, em grupos de 1%.
Em cada simulação, eu fiz com que uma equipe sempre chutasse a bola e a adversária tentasse a conversão de dois pontos para cada probabilidade de sucesso. Também realizei simulações onde ambas as equipes sempre chutavam a bola, para ter um parâmetro de comparação para os resultados da conversão de dois pontos.
A Tabela 1 abaixo mostra os resultados de duas equipes com habilidades equivalentes. A equipe A sempre chuta a bola após um touchdown. A tabela mostra a probabilidade de vitória da equipe B e a média de pontos adicionais marcados por jogo, de acordo com a decisão da equipe B de chutar a bola ou tentar a conversão de dois pontos (2PC), bem como a probabilidade de sucesso dessa tentativa.
Tabela 1 — Equipes Iguais
| Equipe B Estratégia | Equipe B Provavelmente. Ganhar | Média Adicional Pontos |
|---|---|---|
| Chute | 50,00% | 0,0001 |
| 2PC -- 46% | 49,76% | 0,0491 |
| 2PC -- 47% | 49,90% | 0,0000 |
| 2PC -- 48% | 50,05% | 0,0492 |
| 2PC -- 49% | 50,19% | 0,0980 |
| 2 peças -- 50% | 50,33% | 0,1461 |
Note que, com uma probabilidade de sucesso de 47%, os pontos adicionais esperados são de 0,94, tanto para um chute quanto para uma conversão de dois pontos. No entanto, a probabilidade de vitória é 0,1% menor ao optar pela conversão de dois pontos. Acredito que isso se deva ao fato de que, se o chute for errado, o outro time tem a chance de empatar com dois field goals. É importante ressaltar que esse efeito numérico é bastante pequeno, mas favorece uma abordagem conservadora, optando pelo chute, considerando todas as outras variáveis iguais. Em resumo, com duas equipes de nível semelhante, a probabilidade de sucesso na conversão de dois pontos deve ser de pelo menos 49% para optar por ela.
A Tabela 2 abaixo mostra os resultados de duas equipes desiguais, onde a equipe A é mais forte. A equipe A sempre chuta a bola após um touchdown. Ela apresenta as mesmas estatísticas da Tabela 1 acima.
Tabela 2 — Equipe A Mais Forte
| Equipe B Estratégia | Equipe B Provavelmente. Ganhar | Média Adicional Pontos |
|---|---|---|
| Chute | 28,83% | -7,0039 |
| 2PC -- 46% | 29,01% | -7,0519 |
| 2PC -- 47% | 29,16% | -7,0039 |
| 2PC -- 48% | 29,30% | -6,9568 |
| 2PC -- 49% | 29,45% | -6,9083 |
| 2 peças -- 50% | 29,60% | -6,8595 |
A Tabela 2 mostra que a equipe mais fraca deve tentar a conversão de dois pontos em todas as probabilidades de sucesso listadas. Mesmo em 45%, onde o número esperado de pontos totais marcados é menor. Por que isso acontece, você pode perguntar. Isso ocorre porque, em qualquer jogo, a equipe mais fraca deve buscar a variação, enquanto a equipe mais forte deve evitá-la.
A Tabela 3 abaixo mostra os resultados de duas equipes desiguais, onde a equipe B é mais forte. A equipe A sempre chuta a bola após um touchdown. Ela mostra as mesmas estatísticas das Tabelas 1 e 2 acima.Tabela 3 — Equipe B Mais Forte
| Equipe B Estratégia | Equipe B Provavelmente. Ganhar | Média Adicional Pontos |
|---|---|---|
| Chute | 71,17% | 7,0042 |
| 2PC -- 46% | 70,53% | 6,9349 |
| 2PC -- 47% | 70,67% | 7.0030 |
| 2PC -- 48% | 70,82% | 7,0725 |
| 2PC -- 49% | 70,97% | 7.1412 |
| 2 peças -- 50% | 71,12% | 7.2109 |
Observe que a tabela 3 mostra uma probabilidade de vitória da equipe B igual a 71,17% por meio de um chute. Essa probabilidade é menor do que a de todas as outras probabilidades de sucesso apresentadas, mesmo que o número esperado de pontos seja maior com uma probabilidade de sucesso de 49% ou 50%. A razão, novamente, é que equipes mais fracas devem buscar a variação, enquanto as mais fortes devem evitá-la. A tentativa de conversão de dois pontos adiciona volatilidade ao jogo, e é por isso que equipes mais fracas, em igualdade de condições, tendem a ser mais propensas a tentar esse tipo de conversão do que equipes mais fortes.
Quais são as chances do Carolina Panthers terminar a temporada regular com 16 vitórias e nenhuma derrota? Alguma dessas apostas é boa?
Sim, +425?
Sem -550?
Tenho um método para estimar a diferença de pontos esperada para qualquer jogo que se aproxima notavelmente da diferença real, exceto em casos de lesões graves, recuperações, suspensões ou outros imprevistos. Aqui está a fórmula para calcular os pontos esperados de cada equipe:
[(Média de pontos ofensivos) + (Média de pontos sofridos pela equipe adversária)]/2 + (1,5 se jogar em casa, caso contrário -1,5).
A diferença de pontos será (Pontos esperados da equipe visitante) - (Pontos esperados da equipe da casa).
Vamos analisar o jogo da semana 13 contra os Saints como exemplo. Os Panthers são o time visitante. Os Panthers marcaram uma média de 32,3 pontos de ataque por jogo nesta temporada. Os Saints sofreram uma média de 30,8 pontos por jogo. Usando minha fórmula, os Panthers podem esperar marcar (32,3 + 30,8) / 2 - 1,5 = 30,05 pontos.
Em seguida, faça o mesmo para os Saints. Eles marcaram uma média de 23,7 pontos ofensivos por jogo nesta temporada. Os Panthers sofreram uma média de 18,6 pontos por jogo. Minha fórmula resulta em (23,7 + 18,6)/2 + 1,5 = 22,65 pontos marcados pelos Saints.
Portanto, os Panthers podem esperar vencer por 30,05 - 22,65 = 7,4 pontos. Em seguida, use minha Calculadora de Apostas Especiais para determinar a probabilidade de vitória em cada jogo. Minha calculadora perguntará sobre o total de pontos (over/under) da partida, mas descobri que, para determinar quem vencerá o jogo, o que realmente importa é o spread. Para o total, basta inserir a média da NFL nesta temporada, que é 46. Você verá que, para um spread de 7,4 pontos, a linha justa para a vitória do time da casa é +271. Isso significa que a linha justa para os Panthers é -271. Isso equivale a uma probabilidade de vitória de 271/371 = 73,05%.
Em seguida, basta fazer isso para os outros quatro jogos e calcular o produto. Ou você pode simplesmente usar a tabela abaixo.
Semanas 13 a 17 dos Panthers
| Semana | Opondo-se Equipe | Localização | Esperado Pantera Pontos | Esperado Adversário Pontos | Panteras Vencendo Margem | Panteras Justo Linha | Probabilidade Ganhar |
|---|---|---|---|---|---|---|---|
| 13 | Santos | Ausente | 30.05 | 22,65 | 7.4 | -271 | 0,730458 |
| 14 | Falcões | Lar | 28.3 | 19,6 | 8.7 | -323 | 0,763593 |
| 15 | Gigantes | Ausente | 27.05 | 23,85 | 3.2 | -154 | 0,606299 |
| 16 | Falcões | Ausente | 25.3 | 22,6 | 2.7 | -144 | 0,590164 |
| 17 | Bucaneiros | Lar | 30,35 | 19h05 | 11.3 | -458 | 0,820789 |
Multiplicando a coluna de probabilidade, você obtém a probabilidade de ganhar todos os cinco jogos, que é 0,163813. Isso corresponde a uma linha razoável de +510. Portanto, nenhuma das linhas que você citou é boa.
Essa questão foi levantada e discutida no meu fórum no Wizard of Vegas .
Qual foi a última jogada do primeiro tempo da partida entre Panthers e Saints na semana 13 da temporada de 2015?
Acredito que seja chamado de "retorno de ponto extra após touchdown". De acordo com uma mudança de regra em vigor nesta temporada, se uma tentativa de chute após um touchdown falhar, e o time adversário marcar um touchdown, então valerá como dois pontos para o time que pontuou. Antes da temporada de 2015, a bola teria sido considerada morta. Este foi o primeiro, e até agora único, lance desse tipo na NFL. Você pode ver um vídeo no YouTube .
Essa questão foi levantada e discutida no meu fórum no Wizard of Vegas .
Como você provavelmente sabe, o time da UMBC, 16º cabeça de chave, venceu o time da Universidade da Virgínia, 1º cabeça de chave, no torneio de basquete universitário da NCAA. Isso nunca havia acontecido antes nos 34 anos de história do March Madness em seu formato atual. Como isso afeta a probabilidade de preencher um chaveamento perfeito?
Após ajustar meu modelo para esse jogo e todos os outros da temporada de 2018, cheguei a uma probabilidade de um palpite perfeito de 1 em 42.743.890.552. Você pode ler minha estratégia e como cheguei a esse número na minha página Probabilidade de um Palpite Perfeito .
Como faço para converter as probabilidades em apostas esportivas entre as formas americana e europeia de expressá-las?
Vamos considerar que "a" representa as probabilidades expressas à maneira americana e "e" à maneira europeia.
Para ir do estilo americano ao europeu:
Se a>0, então e=1+(a/100).
Se a<0, então e=(a-100)/a.
Para ir do estilo europeu ao americano:
Se e>=2, então a=100×(e-1).
Se e<2, então a=100/(1-e).
Já vi apostas de proposição na casa de apostas esportivas William Hill sobre se algum jogo da Major League Baseball terá um Grand Slam em um determinado dia. Qual é a probabilidade justa e a linha de aposta para isso, considerando o número de jogos disputados?
Para benefício de outros leitores, aqui estão as linhas para um Grand Slam de 11 de maio de 2019. Os títulos das colunas devem dizer "sim" e "não", e não "casa" e "visitante".

Para responder a essa pergunta, analisei todos os jogos da MLB das temporadas de 2011 a 2018. Nessas oito temporadas, houve 858 Grand Slams em 19.440 jogos. Isso resulta em uma média de 0,0441 Grand Slams por jogo. Essa média não é a mesma que a probabilidade de um jogo específico ter um Grand Slam, pois um jogo pode ter mais de um. Usando a distribuição de Poisson, a probabilidade de um jogo específico ter pelo menos um Grand Slam é de 4,3176%.
Com essa probabilidade, é fácil criar a seguinte tabela que mostra a probabilidade e a linha justa para pelo menos um Grand Slam por número de jogos.
Probabilidade de Grand Slam
| Jogos | Probabilidade Grand Slam | Linha justa |
|---|---|---|
| 1 | 4,32% | 2216 |
| 2 | 8,45% | 1084 |
| 3 | 12,40% | 706 |
| 4 | 16,18% | 518 |
| 5 | 19,80% | 405 |
| 6 | 23,27% | 330 |
| 7 | 26,58% | 276 |
| 8 | 29,75% | 236 |
| 9 | 32,78% | 205 |
| 10 | 35,68% | 180 |
| 11 | 38,46% | 160 |
| 12 | 41,12% | 143 |
| 13 | 43,66% | 129 |
| 14 | 46,09% | 117 |
| 15 | 48,42% | 107 |
| 16 | 50,65% | -103 |
Devo acrescentar uma ressalva: minha resposta se baseia nas médias da MLB. Para qualquer dia específico, o jogador deve levar em consideração os jogos que estão sendo disputados. Em particular, quanto maiores as linhas de over/under, maiores as chances de um Grand Slam.
Diversas casas de apostas esportivas, como a MGM em Nova Jersey, estão oferecendo uma aposta totalmente grátis — se a aposta for perdedora, eles reembolsam em DINHEIRO que você pode sacar. É como um reembolso de 100% das perdas em caça-níqueis, mas aplicado a apostas esportivas. Que tipo de aposta devo fazer com essa promoção?
Em qualquer torneio freeroll como este, você deve mirar alto. Se permitirem apostas combinadas, aposte o máximo permitido pela promoção e combine eventos suficientes para atingir o prêmio máximo, que em Las Vegas costuma ser em torno de US$ 100.000.
Se você tiver que apostar em um único evento, escolha a aposta mais improvável que conseguir.
Como exemplo de por que essa estratégia é a melhor, considere a mesma promoção na roleta de duplo zero com uma aposta de $100. Se você fizer uma aposta com probabilidade de 1/1 (ou seja, com chances iguais), o valor esperado de retorno será (18/38) × $200 + (20/38) × $100 = $147,37. No entanto, se você apostar em um único número, poderá esperar receber (1/38) × $3600 + (37/38) × $100 = $192,11.
Vi uma promoção em uma casa de apostas online onde uma aposta no vencedor de um jogo da NFL seria automaticamente considerada vencedora se o time escolhido estivesse vencendo por 17 pontos ou mais. Qual é a vantagem disso?
Esta promoção transformará uma aposta que seria perdedora em vencedora se o time escolhido estiver vencendo por 17 pontos ou mais e depois perder. Um bom exemplo dessa situação é uma aposta no Atlanta Falcons no Super Bowl 51. Em determinado momento do terceiro quarto, os Falcons estavam vencendo por 28 a 3, uma vantagem de 25 pontos. No entanto, eles acabaram perdendo por 28 a 34.
Para responder a essa pergunta, analisei 4.131 jogos disputados em todas as temporadas da NFL de 2000 a 2015. A tabela a seguir mostra a maior desvantagem que o time vencedor teve durante a partida. A coluna de probabilidade exclui os cinco jogos que terminaram empatados.
Superar o maior déficit
| Déficit | Jogos | Probabilidade |
|---|---|---|
| Gravata | 5 | 0,000000 |
| 0 | 1804 | 0,437227 |
| 1 | 100 | 0,024237 |
| 2 | 29 | 0,007029 |
| 3 | 560 | 0,135725 |
| 4 | 235 | 0,056956 |
| 5 | 23 | 0,005574 |
| 6 | 131 | 0,031750 |
| 7 | 622 | 0,150751 |
| 8 | 39 | 0,009452 |
| 9 | 34 | 0,008240 |
| 10 | 195 | 0,047261 |
| 11 | 84 | 0,020359 |
| 12 | 14 | 0,003393 |
| 13 | 49 | 0,011876 |
| 14 | 104 | 0,025206 |
| 15 | 10 | 0,002424 |
| 16 | 6 | 0,001454 |
| 17 | 36 | 0,008725 |
| 18 | 14 | 0,003393 |
| 19 | 2 | 0,000485 |
| 20 | 4 | 0,000969 |
| 21 | 22 | 0,005332 |
| 22 | 0 | 0,000000 |
| 23 | 2 | 0,000485 |
| 24 | 5 | 0,001212 |
| 25 | 1 | 0,000242 |
| 26 | 0 | 0,000000 |
| 27 | 0 | 0,000000 |
| 28 | 1 | 0,000242 |
| Total | 4131 | 1.000000 |
A linha "Empate" representa os cinco jogos nas 16 temporadas que terminaram empatados, então não vamos contá-los. A linha "0" representa os 43,7% dos jogos em que o time vencedor nunca esteve atrás no placar.
A tabela mostra que em 87 jogos uma equipe perdeu por 17 pontos ou mais e depois venceu. Considerando os 4126 jogos resolvidos (ou seja, sem contar os cinco empates), essa probabilidade é de 2,11%.
Considerando que essas situações transformariam uma derrota em vitória, dobramos essa probabilidade para obter um valor de 4,22%. A vantagem da casa nas apostas na linha de dinheiro é aproximadamente a mesma que nas apostas contra o spread, em 4,76%. Subtraindo 4,22%, obtemos uma vantagem da casa muito baixa de 0,54% nesta promoção.
Agora que o March Madness 2023 terminou, como mudou sua probabilidade de acertar todos os palpites e o número de vitórias esperadas por posição no ranking?
Minha estratégia para um chaveamento perfeito é escolher o time com a melhor classificação (ou seja, com um número de classificação menor) em todos os jogos. No final, quando chegar ao confronto direto entre os dois melhores colocados, escolho aleatoriamente. Baseado em dados de 38 temporadas. Aqui estão algumas probabilidades para cada possível jogo:
- 1º vs. 16º cabeça de chave = 99,31%
- 2º vs. 15º cabeça de chave = 93,06%
- Cabeça de chave 3 vs. 14 = 84,72%
- Cabeça de chave 4 vs. 13 = 78,47%
- Cabeça de chave 5 vs. 12 = 64,58%
- 6º vs. 11º cabeça de chave = 62,50%
- 7º vs. 10º cabeça de chave = 60,42%
- Cabeça de chave 8 vs. 9 = 51,39%
Para sobreviver à primeira rodada, você precisaria vencer cada um dos oito jogos listados acima quatro vezes. A probabilidade disso é de 1/4354.
Aqui estão os vários confrontos possíveis na segunda rodada, supondo que você chegue até lá usando essa estratégia.
- 1º vs. 8º cabeça de chave = 80,00%
- 2º vs. 7º cabeça de chave = 69,51%
- Cabeça de chave 3 vs. 6 = 60,00%
- Cabeça de chave 4 vs. 5 = 56,00%
Para sobreviver à segunda rodada, você precisaria vencer cada um dos quatro jogos listados acima quatro vezes. A probabilidade disso é de 1/811.
Aqui estão os vários confrontos possíveis na rodada 3, supondo que você chegue até lá usando esta estratégia.
- 1º vs. 4º cabeça de chave = 73,44%
- 2º vs. 3º cabeça de chave = 60,71%
Para sobreviver à segunda rodada, você precisaria vencer cada um dos jogos listados acima quatro vezes. A probabilidade disso é de 1/54.
Na rodada 4, haverá jogos entre o cabeça de chave 1 e o cabeça de chave 2. A probabilidade de o cabeça de chave 1 vencer é de 53,73%. A probabilidade de isso acontecer quatro vezes é 0,5373 ÷ 4 = 0,112355.
Na rodada 5, haverá dois jogos 1 contra 1. A probabilidade de vencer cada um é 1/2, portanto a probabilidade de vencer os dois é 1/4.
Na rodada 6, haverá um jogo 1 contra 1. A probabilidade de vitória é de 1/2.
O produto de todas essas probabilidades resulta em uma probabilidade de um colchete perfeito de 1 em 13.569.150.522.
Para responder às suas outras perguntas, aqui está a média de vitórias por equipe, por classificação.
- Cabeça de chave número 1 = média de 3,29 vitórias
- Cabeça de chave número 2 = média de 2,32 vitórias
- Cabeça de chave número 3 = média de 1,85 vitórias
- Cabeça de chave número 4 = média de 1,55 vitórias
- Cabeça de chave número 5 = média de 1,16 vitórias
- Cabeça de chave número 6 = média de 1,07 vitórias
- Cabeça de chave número 7 = média de 0,9 vitórias
- Cabeça de chave número 8 = média de 0,74 vitórias
- Cabeça de chave número 9 = média de 0,59 vitórias
- Cabeça de chave número 10 = média de 0,61 vitórias
- Cabeça de chave número 11 = média de 0,63 vitórias
- Cabeça de chave número 12 = média de 0,51 vitórias
- Cabeça de chave número 13 = média de 0,25 vitórias
- Cabeça de chave número 14 = média de 0,16 vitórias
- Cabeça de chave número 15 = média de 0,11 vitórias
- Cabeça de chave número 16 = média de 0,01 vitórias


