Texas Hold'em - Perguntas frequentes
Adoro seu site! Sou formado em matemática e conto cartas no blackjack , tendo viajado várias vezes para Las Vegas . Gostaria de começar a usar minhas habilidades matemáticas para jogar pôquer. Já assisti a partidas de pôquer de longe em Las Vegas e agradeceria qualquer conselho ou explicação sobre as regras. Posso obter uma vantagem semelhante à contagem de cartas no blackjack?
Primeiramente, gostaria de deixar claro que não sou especialista em pôquer. Não é segredo que o Texas Hold'em é a modalidade mais popular. Nesse jogo, há cinco cartas comunitárias e apenas duas cartas fechadas por jogador, o que dá mais margem para quem tem habilidade em calcular probabilidades. No entanto, mesmo o melhor gênio da matemática pode se tornar um jogador de pôquer ruim se não conseguir ler os outros jogadores ou se os outros jogadores conseguirem lê-lo facilmente (e acredito que ambos os casos sejam verdadeiros para mim).
Tenho uma pergunta simples. Sei que você é o Mago das Probabilidades, mas preciso de ajuda. Jogo Craps e Texas Hold'em nos cassinos. Sinto que poderia ser uma força intimidadora (AUMENTANDO, ASSIM, MINHAS CHANCES DE GANHAR) se conseguisse descobrir como embaralhar minhas fichas de pôquer. Já pratiquei, mas simplesmente não consigo. Gostaria que você me indicasse um caminho para aprender isso. Obrigado pelo seu tempo.
Você perguntou para a pessoa certa! Sou bastante bom em embaralhar fichas de pôquer. Infelizmente, não tenho muitas oportunidades de demonstrar isso, pois quando jogo com fichas, geralmente é para contar cartas ou ler a carta fechada, e em nenhum dos casos quero parecer um profissional. Enfim, comece com uma pilha de 10 fichas. Depois, corte-as ao meio, colocando duas pilhas de 5 fichas lado a lado. Imagine as duas pilhas formando um 8. Posicione o 8 em um ângulo de aproximadamente 45 graus em relação ao seu plano de simetria. Coloque o polegar na parte inferior do 8, o indicador onde as duas pilhas se encontram e os outros três dedos na parte superior do 8. Todos os cinco dedos devem estar quase tocando a mesa. Em seguida, usando o indicador, levante delicadamente as duas pilhas enquanto os outros quatro dedos as empurram suavemente uma contra a outra. Quando o indicador estiver a cerca de meio centímetro da parte inferior da mesa, afaste-o rapidamente e continue empurrando as pilhas com os outros quatro dedos. É preciso prática. Recomendo comprar 10 fichas de argila de boa qualidade e praticar em casa ou no trabalho. Durante os intervalos comerciais ou sempre que tiver um minuto livre, você pode praticar. Antes que perceba, estará embaralhando fichas como um profissional e intimidando seus colegas jogadores de pôquer.
Como você decidiu simular 5.197.920.000 partidas de 10 mãos cada para a sua página de Texas Hold'em ? Esse número é significativo?
Configurei meu simulador para funcionar por um determinado período de tempo. A cada 10.000 movimentos do ponteiro de ponteiro, o programa verifica o tempo e, quando ultrapassa o tempo final definido, ele para onde estiver.
Fico feliz em saber que você começou a jogar Texas Hold'em. Eu adoro o jogo e estou ganhando online, mas por pouco. Já li mais de uma dúzia de livros sobre pôquer, mas queria saber sua opinião sobre alguns pontos.
- Qual a sua opinião sobre "Posição"? Exemplo: Você acha que realmente existem mãos lucrativas em posições tardias, mas que nunca deveriam ser jogadas em posições iniciais?
- E quanto às "Pot Odds"? Eu entendo o conceito, mas já desisti de muitas mãos que seriam vencedoras, simplesmente porque não tinha as odds corretas para continuar na mão e tentar um flush... Os gráficos no seu site sugerem que as mãos iniciais mais fortes têm um certo "Valor Esperado" se não forem descartadas. Vocês recomendam continuar jogando com essas mãos até o river, a menos que seja óbvio que você está perdendo (independentemente das pot odds)?
Obrigado pelo seu tempo.
Primeiramente, ainda sou iniciante, então não sou a pessoa mais indicada para responder. A posição é muito importante no pôquer. Quanto mais tarde você jogar, mais informações terá sobre as cartas dos seus oponentes quando chegar a sua vez. Por exemplo, se você formar um par na carta do meio do flop e todos derem check para você, e você for o último a jogar, então você pode se sentir confortável em aumentar a aposta sabendo que provavelmente ninguém formou um par na carta mais alta. No entanto, você verá como as coisas se desenrolam ao longo da mesa. Se você tiver uma mão boa, mas não excepcional, e aumentar a aposta, ela pode ser re-aumentada por jogadores com mãos mais fortes. Se você der check com uma mão assim, todos os outros jogadores podem dar check e você perderá a chance de aumentar o pote e intimidar os outros jogadores. Portanto, não aposte apenas o valor das suas cartas; em vez disso, você precisa compará-las com as cartas de todos os outros jogadores. Quanto mais tarde você jogar, mais informações terá sobre as cartas dos outros jogadores quando chegar a sua vez.
As probabilidades do pote são um conceito importante. Como em qualquer forma de jogo de azar, o valor de uma aposta depende da sua probabilidade de ganhar, do valor da aposta e do valor do ganho. A tabela a seguir mostra algumas situações comuns. A coluna de probabilidade mostra a probabilidade de fazer uma sequência ou um flush. A coluna de probabilidades do pote mostra o número mínimo de unidades de aposta já presentes no pote para que a aposta seja vantajosa, assumindo que você certamente ganhará se fizer a sua mão (a menos que você tenha o flush máximo, o que é uma grande incógnita).
Sorteios frequentes
| Mão | Depois | Probabilidade de Fazendo mão | Probabilidades do pote |
|---|---|---|---|
| 4 para uma descarga | Fracasso | 34,97% | 1,86 |
| 4 para uma reta externa | Fracasso | 31,45% | 2.18 |
| 4 para uma reta interna | Fracasso | 16,47% | 5.07 |
| 4 para uma descarga | Vez | 19,57% | 4.11 |
| 4 para uma reta externa | Vez | 17,39% | 4,75 |
| 4 para uma reta interna | Vez | 8,70% | 10,50 |
Há muitos outros fatores a considerar. Poderíamos escrever um livro inteiro sobre isso, e de fato, muitas pessoas já o fizeram. Pessoalmente, recomendo "Get the Edge at Low-Limit Texas Hold 'em", de Bill Burton, como um livro introdutório sobre Hold'em. Sobre as minhas tabelas, não, definitivamente não confie em uma boa mão inicial durante toda a partida. Haverá muitas vezes em que você deve desistir de um par de ases. Minhas tabelas servem apenas para ajudar o jogador a apostar antes do flop. Após o flop, o valor esperado da sua mão provavelmente mudará substancialmente.
Quando vocês vão fazer alguma coisa em relação aos jackpots de bad beat?
Me perguntam sobre jackpots de bad beat cerca de uma vez por mês. Quando tiver tempo, pretendo adicionar uma seção sobre isso ao meu site. Minha hesitação é que acabem me perguntando sobre todos os jackpots de bad beat em todas as salas de poker do mundo.
Numa partida amistosa de pôquer em casa, restavam apenas dois jogadores numa mão de Texas Hold'em. Eu estava fora da mão e olhei as cartas do meu vizinho. Ele estava prestes a desistir quando eu disse, sem pensar, que ele tinha uma sequência, o que obviamente ele não tinha percebido. O outro jogador, com uma mão mais fraca, disse que isso era uma quebra de etiqueta do pôquer. Ele estava certo?
Sim, ele estava. No pôquer, se você não estiver na mão, não jogue. Não me incomoda que jogadores que ainda estão na partida mostrem suas cartas para outros jogadores, mas ainda assim não gosto. No entanto, se você não estiver na mão e vir outras cartas, deve ficar calado. O que é ainda mais irritante é quando alguém desiste da mão e depois começa a dar conselhos para a namorada que ainda está jogando. Oferecer conselhos é uma grande quebra de etiqueta se você tem informações que o jogador não tem, ou seja, as cartas que você descartou.
Um torneio de Hold'em começa com a disputa pela carta mais alta no botão. A carta mais alta vence, e espadas vence copas, que vence ouros, que vence paus. Qual é a carta média que vence em uma mesa de 10 pessoas? Tentei simular atribuindo um valor numérico a cada carta, mas não consigo descobrir de jeito nenhum! Obrigado e continuem assim!
Para simplificar a questão, digamos que as cartas estejam numeradas de 1 a 52. A tabela a seguir mostra a probabilidade de que a 10ª à 52ª carta seja a de maior valor. Existem combin (x-1,9) maneiras de escolher 9 números abaixo de x e combin(52,10) maneiras de escolher qualquer número entre 52. Portanto, a probabilidade de x ser o maior número pode ser expressa como combin(x-1,9)/combin(52,10). A coluna "esperado" representa o produto da probabilidade pelo número de bolas. A soma da coluna "esperado" mostra que, em média, a bola de maior valor será 48,18. Arredondando para a carta mais próxima, a carta de maior valor esperado é o rei de espadas.
A maior das 10 cartas
| Carta mais alta | Probabilidade | Esperado |
|---|---|---|
| 10 | 0,000000000063 | 0,000000000632 |
| 11 | 0,000000000632 | 0,000000006953 |
| 12 | 0,000000003477 | 0,000000041719 |
| 13 | 0,000000013906 | 0,000000180784 |
| 14 | 0,000000045196 | 0,000000632742 |
| 15 | 0,000000126548 | 0,000001898227 |
| 16 | 0,000000316371 | 0,000005061939 |
| 17 | 0,000000723134 | 0,000012293281 |
| 18 | 0,00000153666 | 0,000027659882 |
| 19 | 0,00000307332 | 0,000058393084 |
| 20 | 0,000005839308 | 0,000116786168 |
| 21 | 0,000010616924 | 0,000222955411 |
| 22 | 0,000018579618 | 0,000408751587 |
| 23 | 0,00003144243 | 0,000723175884 |
| 24 | 0,00005165542 | 0,001239730087 |
| 25 | 0,000082648672 | 0,002066216811 |
| 26 | 0,000129138551 | 0,003357602319 |
| 27 | 0,000197506019 | 0,005332662506 |
| 28 | 0,000296259028 | 0,008295252787 |
| 29 | 0,000436592252 | 0,012661175306 |
| 30 | 0,000633058765 | 0,01899176296 |
| 31 | 0,000904369665 | 0,028035459607 |
| 32 | 0,001274339073 | 0,040778850337 |
| 33 | 0,001772993493 | 0,058508785267 |
| 34 | 0,002437866053 | 0,082887445794 |
| 35 | 0,003315497832 | 0,116042424112 |
| 36 | 0,004463170158 | 0,160674125694 |
| 37 | 0,005950893544 | 0,220183061136 |
| 38 | 0,007863680755 | 0,298819868684 |
| 39 | 0,010304133403 | 0,401861202713 |
| 40 | 0,013395373424 | 0,535814936951 |
| 41 | 0,017284352805 | 0,708658464999 |
| 42 | 0,022145577031 | 0,930114235312 |
| 43 | 0,028185279858 | 1,211967033891 |
| 44 | 0,035646089232 | 1,568427926212 |
| 45 | 0,044812226463 | 2.016550190844 |
| 46 | 0,056015283079 | 2,576703021634 |
| 47 | 0,069640622206 | 3,273109243697 |
| 48 | 0,086134453782 | 4,134453781513 |
| 49 | 0,106011635423 | 5.194570135747 |
| 50 | 0,129864253394 | 6,493212669683 |
| 51 | 0,158371040724 | 8.076923076923 |
| 52 | 0,192307692308 | 10 |
| Total | 1 | 48,181818181818 |
Embora você não tenha perguntado, a carta mediana é o ás de paus. A probabilidade da carta mais alta ser menor que o ás de paus é de 41,34%, exatamente no ás de paus é de 10,60% e maior que o ás de paus é de 48,05%.
Agradeceria imensamente se pudesse responder à minha pergunta. Enviei e-mails para vários profissionais de pôquer, incluindo o canadense (Blount). Nenhum deles respondeu. A maioria sequer respondeu, inclusive o Blount. Minha pergunta é: poderia me dizer a fórmula para calcular as probabilidades e porcentagens de receber as duas primeiras cartas no Hold'em e a porcentagem de essa mão específica vencer as outras mãos — supondo que você saiba quais são — como as que vemos na TV? Eu já conheço a fórmula e o método mais simples para calcular se você completa a mão após o flop. Sei da existência da calculadora de pôquer, mas gostaria de saber a fórmula para meu próprio conhecimento. A gente ouve falar que os profissionais sabem todas as probabilidades. Estou começando a achar que é tudo balela, porque ninguém respondeu à minha pergunta. Muito obrigado por dedicar seu tempo para ler isto.
Não existe uma fórmula simples. Pessoalmente, meu programa percorre todas as cartas restantes e registra o número de mãos vencedoras de cada jogador, calculando uma porcentagem com base nesses totais. Imagino que todos os outros façam o mesmo ou usem simulação aleatória.
(Bluejay acrescenta: Quanto à sua dúvida de que os profissionais realmente conhecem as probabilidades do pôquer porque não lhe responderam, não lhe ocorreu que outra explicação provável é que eles não se importaram em servir como um serviço de ajuda gratuito para o mundo todo? Britney Spears deve ser uma fraude, porque ela também nunca me respondeu.)
No Texas Hold'em, se um jogador acidentalmente mostrar suas cartas antes do término da rodada de apostas, a mão desse jogador é considerada inválida?
Não. Ainda seria uma mão viva.
Sou iniciante no Texas Hold'em e meu primeiro livro sobre o assunto foi "Play Poker Like the Pros" , de Phil Hellmuth. Depois de comparar as dez melhores mãos de Hold'em dele com as suas, notei diferenças significativas. Por exemplo, ele coloca 7-7 como a décima melhor mão, enquanto você a classifica bem abaixo na lista. Há outras discrepâncias importantes. Confio nas suas análises de diversos jogos de cassino e gostaria de saber como suas listas podem ser tão diferentes. Obrigado.
É difícil dar conselhos sobre pôquer porque o comportamento dos outros jogadores é desconhecido. Meu modelo assume que todos os jogadores permanecem na mão até o final, por uma questão de simplicidade. Embora eu respeite a opinião de Phil , o livro "Get the Edge at Low-Limit Texas Hold'em", de Bill Burton, lista as mãos em três grupos, e 7-7 é o menor par a ser jogado apenas em posições intermediárias ou finais. Ele diz que 6-6 só deve ser jogado em posições finais. Em outras palavras, ele também não parece ter uma opinião muito positiva sobre 7-7.
Em "Ken Warren Teaches Texas Hold 'Em", ele afirma que contra um par de ases (onde os naipes são da mesma cor), nenhuma outra mão vence com mais frequência do que 6/5 do mesmo naipe e de cor oposta. Concordo que essa mão vence 22,89% das vezes na situação descrita. No entanto, existem doze maneiras de organizar um par de ases, e apenas duas delas incluem a situação acima. Minha pergunta é, então: qual é a melhor mão inicial contra dois ases aleatórios?
A melhor mão contra dois ases aleatórios são os outros dois ases. Além disso, usando minha calculadora de Hold'em para 2 jogadores, podemos ver que o valor esperado (probabilidade de ganhar menos probabilidade de perder) é maior com um 5 e um 6 do mesmo naipe, independentemente de um dos ases ser do mesmo naipe que o 5 e o 6. Portanto, contra um par de ases aleatórios, o 5 e o 6 do mesmo naipe ainda são melhores. Corrigindo sua observação, se você tem um 5 e um 6 do mesmo naipe e sabe que alguém tem um par de ases, há 50% de chance de que um deles tenha ases do mesmo naipe que você.
Você consideraria fazer uma análise sobre o Texas Hold'em Bonus? Esse jogo é muito popular em Atlantic City e também está presente no Flamingo, em Las Vegas. Obrigado.
Por coincidência, tenho quatro computadores rodando esse jogo sem parar neste momento. O número de combinações possíveis é tão grande que são necessários cerca de 56 dias de processamento para analisá-las todas. Devo concluir a análise por volta de 20 de outubro.
O Party Poker adicionou uma aposta paralela no Hold'em . Ela paga 7 para 1 se o flop for todo vermelho ou todo preto. (Você precisa escolher a cor correta.) Essa aposta é uma aposta para trouxas, ou eu deveria perguntar o quão ruim ela é? Obrigado pelo ótimo site.
Obrigado pelo elogio. A probabilidade de que o flop seja todo igual a uma determinada cor é combin (26,3)/combin(52,3) = 2600/22100 = 2/17 = 11,765%. O retorno esperado desta aposta é (2/17)*7 - (15/17) = -1/17 = -5,882%.
Estou confuso com sua afirmação na coluna de 25 de setembro de 2005 de que um 5/6 do mesmo naipe é a melhor mão contra um par de ases no Hold'em. Embora seu programa esteja indubitavelmente correto e em consonância com todos os outros programas, ainda estou um pouco intrigado com o motivo de 5/6 ser melhor que 6/7 (no sentido de perder menos em vez de ganhar mais), especialmente quando há várias mãos óbvias em que é pior, principalmente o fato de que a sequência A234 perde para quatro ases quando essa é a quinta carta, enquanto a sequência correspondente 2345 não tem esse problema. Há algumas outras anomalias que estou analisando, mas o que me interessa é que o que parece ser um problema de lógica pura está longe de ser simples e requer o auxílio de uma máquina para guiar a intuição.
Bem, um 5/6 do mesmo naipe contra um par de ases, ambos de naipes diferentes, vencerá 22,87% das vezes, empatará 0,37% e perderá 76,75%. Um 6/7 do mesmo naipe vencerá 22,88% das vezes, empatará 0,32% e perderá 76,80%. Portanto, o 6/7 do mesmo naipe vencerá 0,01% mais. No entanto, o 5/6 do mesmo naipe é melhor porque empata 0,05% mais. A razão para isso parece estar relacionada às sequências. Haverá mais esperas para formar uma sequência na mesa se todas as cartas do meio estiverem no baralho. Remover um 7, em vez de um 5, torna mais difícil formar sequências com as cartas restantes, tornando os empates menos prováveis e, portanto, o valor esperado menor.
No pôquer Hold'em , queimar cartas afeta as probabilidades? Queimar cartas afeta as probabilidades e o jogo em geral?
Não. As probabilidades não se alteram em nenhuma carta obtida ao queimar cartas.
O Party Poker oferece um jackpot para mãos altas, concedido às mesas que formam um Royal Flush. Quais são as chances de uma mesa formar um Royal Flush em um jogo de Texas Hold'em com 10 jogadores?
Se assumirmos que todas as mãos são jogadas até o final, a probabilidade de qualquer jogador ter um royal flush é 4 * combin (47,2) / combin(52,7) = 1 em 30.940. Para simplificar, vamos assumir que cada mão é independente. A probabilidade de pelo menos um jogador em 10 ter um royal flush seria 1 - (1 - (1 / 30.940)) / 10 = 0,00032, ou 1 em 3094.
Parece que temos um debate no escritório sobre mostrar as cartas no Texas Hold'em. Um jogador pode mostrar suas cartas fechadas para a mesa se decidir desistir, mesmo que ainda haja jogadores apostando? Existe alguma regra específica sobre isso?
Isso é uma péssima demonstração de etiqueta no pôquer. Se você fizesse isso em Las Vegas, provavelmente seria avisado para não repetir na primeira vez. Na segunda vez, provavelmente seria convidado a se retirar da mesa.
No seu artigo sobre o bônus de Texas Hold'em, notei que você mencionou que a única parte da estratégia que quantifiquei é que o jogador deve desistir de mãos não-suitadas de 2/3 a 2/7 em qualquer conjunto de regras, e de mãos não-suitadas de 3/4 apenas nas regras de Atlantic City. Esses são os critérios que você criou para sua simulação? Também gostaria de saber como você determina se deve apostar no turn ou no river. Estou tentando descobrir qual seria exatamente a jogada "ótima". Gostaria também de saber o que exatamente você quer dizer com valor "esperado" das mãos iniciais. Resumindo, minha pergunta é: como você determinou a estratégia ótima para este jogo?
Sei que deve ser frustrante declarar a vantagem da casa em um jogo com estratégia ideal, mas não especificar qual é essa estratégia, como acontece no Texas Hold'em Bonus. O motivo é que eu também não sei qual é a estratégia ideal. O número de combinações na maioria dos jogos de pôquer é tão vasto que seria uma tarefa tediosa e demorada quantificar exatamente qual é a estratégia correta. Em vez disso, programo meu computador para percorrer todos os conjuntos de cartas possíveis e fazer a jogada com o maior valor esperado. O valor esperado é o quanto o jogador pode esperar ganhar (positivo) ou perder (negativo). Isso reduz bastante o número de linhas de código necessárias. Portanto, não há simulação aleatória. Meu programa prevê o futuro percorrendo todas as combinações de cartas possíveis e escolhendo a jogada que resulta na maior vitória ou na menor perda.
É necessário revelar as cartas se você pagar uma aposta total de um jogador? Já vi isso acontecer várias vezes na televisão, mas posso simplesmente esperar até o final da mão?
Segundo diversas fontes, revelar as cartas é obrigatório em jogos de torneio, mas opcional em jogos a dinheiro.
Na sua coluna de 20 de março, você respondeu a uma pergunta sobre revelar a mão de Hold'em depois de um all-in e quando todas as apostas terminam. Você mencionou que seu amigo estava meio inseguro, então posso te dizer que em praticamente todas as principais salas de pôquer dos Estados Unidos, a regra é a seguinte: em um torneio de NL, você DEVE revelar sua mão assim que todas as apostas forem concluídas (ou seja, todos os jogadores restantes estiverem all-in). Isso acelera o jogo, pois permite que a mão vencedora seja determinada muito mais rapidamente. Em um jogo a dinheiro de NL, revelar a mão de all-in é OPCIONAL... na verdade, fazer isso é sinal de novato e alguns consideram rude revelá-la antes do river. Então é isso. - Pete de Nova York
Gostaria de responder à pergunta da semana passada sobre revelar as cartas em uma situação de all-in. Acredito ter lido que uma das principais razões para exigir que as cartas sejam mostradas em uma situação como a descrita acima é mais específica para torneios. Exigir que as cartas sejam mostradas ajuda a identificar possíveis conluios e a transferência de fichas de um jogador para outro para ajudar um jogador específico a obter vantagem em fichas.
Agradeço a ambos pela correção.
Fiz uma aposta all-in após o flop. O único jogador restante na mão pensou por alguns segundos e me mostrou as cartas dele. As cartas nunca tocaram a mesa, ele não disse uma palavra, mas interpretei isso como um sinal de desistência. Então, descartei minhas cartas e peguei as fichas, e ele afirmou que ainda não havia desistido. Agora que ele viu minhas duas cartas, decidiu pagar e ganhou com a carta do river. Isso é legal ou não?
O pôquer é um dos meus jogos mais fracos quando se trata de apostas, então recorro novamente ao JB para esta. Aqui está o que ele disse.
Essa jogada é completamente ilegal. Sempre que alguém mostra suas cartas para um oponente, a mão é encerrada. A única exceção é quando ambos os jogadores declaram "all-in". Nesse momento, ambas as mãos são mostradas e a mão é concluída. Nesse caso, o jogador que mostrou as cartas para o oponente perde a mão e o outro jogador vence.Depois de receber essa resposta, lembrei-me de uma cena de um filme, acho que era Stuey , em que um jogador se oferece para virar uma de suas cartas, escolhida pelo outro jogador, por 100 dólares. Perguntei ao JB se a cena era realista. Aqui está a resposta dele para essa pergunta.
Isso sempre acontecia em torneios e era perfeitamente aceitável naquela época. Foi por volta de 2001 ou 2002 que essa regra foi formalmente alterada em quase todas as salas de poker. Eu estava em um torneio na semana passada e estava com poucas fichas. Dei all-in com AQ suited. Todos desistiram até o big blind, que tinha muitas fichas. Depois de pensar por uns dois minutos, ele me mostrou o KQ que tinha e voltou a pensar se deveria pagar. Chamei o supervisor e disse que ele havia me mostrado as cartas antes de tomar uma decisão e que a mão deveria ser considerada morta. Ele concordou comigo, a mão foi automaticamente declarada morta e ele recebeu uma penalidade de cinco minutos, durante a qual teve que sair da mesa, o que lhe custou cerca de cinco mãos. Os blinds e antes eram altos, então a penalidade lhe custou vários milhares de fichas de torneio.
Na sua coluna recente "Pergunte ao Mago" , surgiu uma pergunta sobre um jogador que mostra as cartas antes de declarar uma decisão no Hold'em. Dependendo das regras da casa, isso pode ser permitido em uma situação de heads-up, onde nenhum outro jogador está envolvido (por exemplo: uma mão em um jogo de ring game que chegou aos dois jogadores restantes, OU um torneio heads-up). Em um torneio padrão, você não pode expor suas cartas antecipadamente (mesmo que esteja em um heads-up com outro jogador), pois, teoricamente, isso afetaria todos os outros jogadores ainda na disputa.
Você é a terceira pessoa a afirmar que a resposta de JB estava incorreta. Para obter uma terceira opinião imparcial, perguntei ao supervisor de pôquer do hotel/cassino Red Rock. Ele disse que revelar as cartas não é permitido em torneios ou se mais de dois jogadores ainda estiverem na mão. No entanto, com apenas dois jogadores restantes em uma mão de cash game, se um deles quiser ser imprudente e revelar suas cartas, isso seria permitido no Red Rock. Mais tarde, fiz a mesma pergunta no Wynn e a resposta foi a mesma.
Uma aposta paralela cada vez mais comum que tenho visto em jogos de Texas Hold'em é a aposta no "valor" total do flop, onde o valor de uma carta é atribuído pelas regras do Blackjack (ou seja, A=11, KQJ10=10, as demais são as cartas com valor nominal). Os jogadores têm a opção de escolher um ou mais valores totais, colocando uma aposta paralela no pote. O jogo continua até que o flop atinja um valor que seja coberto por um jogador (portanto, um flop KK4 enviaria o pote para um jogador que apostou em 24). Matematicamente, qual é o melhor número para apostar? Na maioria dos jogos que joguei, há a estipulação de que não se pode apostar em 30, o que levaria a pensar que seria o "melhor" número para apostar, mas considerando que 30 tem um número muito limitado de combinações possíveis (três cartas de valor 10, A-9-10 ou AA-8), não tenho certeza se isso é verdade. Além disso, mãos em que mais jogadores têm cartas de valor dez e ases têm maior probabilidade de ver o flop. Você teria interesse em fazer uma análise dessa aposta paralela?
Vou assumir que, se ninguém ganhar no flop, as apostas são reembolsadas ou o próximo flop é usado para resolvê-las, em vez de usar as cartas do turn e do river. Vou ignorar a regra de que, se todos desistirem, a aposta não é resolvida. Claramente, essa regra ajuda os totais mais baixos, mas considerá-la na análise a tornaria complicada e subjetiva. Dito isso, a tabela abaixo mostra a probabilidade de cada total. Como você pode ver, a melhor aposta seria em um total de 23, com uma probabilidade de 8,3982%.
Pontos de Blackjack no Flop
| Total | Combinações | Probabilidade |
| 33 | 4 | 0,000181 |
| 32 | 96 | 0,004344 |
| 31 | 504 | 0,022805 |
| 30 | 840 | 0,038009 |
| 29 | 784 | 0,035475 |
| 28 | 920 | 0,041629 |
| 27 | 1108 | 0,050136 |
| 26 | 1264 | 0,057195 |
| 25 | 1472 | 0,066606 |
| 24 | 1652 | 0,074751 |
| 23 | 1856 | 0,083982 |
| 22 | 1800 | 0,081448 |
| 21 | 1508 | 0,068235 |
| 20 | 1408 | 0,06371 |
| 19 | 1336 | 0,060452 |
| 18 | 1196 | 0,054118 |
| 17 | 1080 | 0,048869 |
| 16 | 896 | 0,040543 |
| 15 | 740 | 0,033484 |
| 14 | 512 | 0,023167 |
| 13 | 352 | 0,015928 |
| 12 | 268 | 0,012127 |
| 11 | 200 | 0,00905 |
| 10 | 136 | 0,006154 |
| 9 | 92 | 0,004163 |
| 8 | 48 | 0,002172 |
| 7 | 24 | 0,001086 |
| 6 | 4 | 0,000181 |
Seu site é incrível, aprendi muito com ele. No flop do pôquer Hold'em, se você tem 20 cartas que formam a mão vencedora, por que a porcentagem de você completar a mão até o river é de 67,5% e não de 86% (20/47 + 20/46)? Procurei em todos os lugares e não consigo entender, mesmo sabendo que provavelmente é algo muito básico. Agradeceria muito a ajuda, obrigado!
Obrigado! Seu método conta duas vezes, pois você consegue duas das 20 cartas necessárias. A probabilidade de conseguir uma das 20 cartas necessárias no turn é 20/47 = 0,4255. A probabilidade de não conseguir no turn e conseguir no river é (27/47)*(20/46) = 0,2498. Portanto, a probabilidade total é 0,4255 + 0,2498 = 0,6753.
Não entendo muito de pôquer, mas acho divertido, então talvez você possa me esclarecer uma dúvida. Em uma viagem recente a Las Vegas com minha esposa, ficamos no Arizona Charlie's Decatur. Escolhemos o hotel porque eles anunciavam mesas de Hold'em de $2 a $4 no site. Na nossa primeira manhã, fomos até a sala de pôquer e nos inscrevemos para jogar $2-$4. Percebi que o funcionário do pôquer estava anotando nossos nomes nas colunas de $4-$8. Então, expliquei que queríamos jogar $2-$4 (havia uma coluna com a inscrição “$2-$4” na mesma folha). Ele disse que era $2-$4: $2 antes do flop, $4 depois do flop e $8 depois do turn e do river. Expliquei o que eu queria dizer com $2-$4: $2 antes e depois do flop e $4 depois do turn e do river. Ele riu de nós como se não soubéssemos do que estávamos falando e disse que não era assim que o jogo funcionava. Acabamos jogando pôquer no Gold Coast pelo resto da viagem. Esse tipo de aposta é normal em salas de pôquer? (Acabei dizendo ao supervisor da sala de pôquer que se pudéssemos bancar uma partida de Hold'em de US$ 4 a US$ 8, não estaríamos hospedados no Arizona Charlie's.)
Concordo que um jogo "2/4" significa que as apostas são de $2 antes do turn e $4 depois do turn. No entanto, o small blind provavelmente é de $1. Parece que quando o Arizona Charlie's chama um jogo de "2/4", eles estão se referindo aos blinds, o que significaria um small blind de $2 e um big blind de $4, o que implicaria apostas de $8 após o turn. Nunca ouvi esse uso antes, então não te culpo por estar surpreso.
P.S.: Mais tarde, recebi a seguinte mensagem de Anthony, um supervisor da sala de pôquer.
Sou supervisor de uma sala de poker. Estou escrevendo para informar sobre a terminologia correta para os limites no Texas Hold'em. Quando um jogo é mencionado como $2/$4, está se referindo às apostas. (Um jogo só é mencionado pelos blinds se for No-Limit.) $2 no pré-flop e pós-flop, $4 no turn e no river. Um jogo listado como $2/$4/$8 (que é exatamente o que suspeito que o autor da carta anterior estava se referindo) significa $2 no pré-flop, $4 no pós-flop, $8 no turn e no river. Também é possível que um jogo seja listado como $2/$4/$6/$8. Estou apenas repassando a informação, pois bons supervisores de poker querem que as pessoas tenham o máximo de informações possível.
Considere a mão inicial 6,5 suited no Hold'em. De acordo com as probabilidades publicadas, em um jogo de 2 jogadores, essa mão está classificada em 128º lugar entre 169 mãos possíveis. Mas em um jogo de 10 jogadores, essa mão está classificada em 61º lugar entre 169 mãos possíveis. Estou muito curioso para saber o porquê disso. Obrigado pela ajuda.
Grande parte do valor dos conectores suited vem da probabilidade relativamente alta de formar uma sequência, um flush ou um straight flush. Essas são mãos premium, que geralmente vencem contra qualquer número de jogadores. Em um jogo de dois jogadores, você só recebe o dinheiro de uma pessoa, mas em um jogo de 10 jogadores, você pode maximizar o pote.
Tenho uma dúvida que gerou muita discussão no nosso grupo. Ela diz respeito a jogadores que não têm fichas suficientes para pagar o small blind (ou big blind). Exemplo: Em um torneio, com blinds de 20/40. O jogador na posição de small blind tem apenas 15 fichas. Esse jogador deve ser eliminado por não conseguir pagar o valor do blind, ou deve ser permitido que ele jogue (all-in) com as fichas que possui?
Um jogador pode pagar menos nessa situação, mas só poderá ganhar o valor da sua aposta de cada um dos outros jogadores que pagaram o small blind. No exemplo acima, 15 fichas de cada jogador que pagou o small blind seriam colocadas no pote. Todo o restante do dinheiro seria colocado em um pote paralelo, do qual o jogador com menos fichas não teria direito.
Meus agradecimentos a Ashley Adams pela ajuda com esta questão.
No Colorado, cada aposta tem um limite máximo de $5. No Texas Hold'em Bonus, o ante mínimo/máximo é de $5 e o mínimo/máximo para o flop, turn e river também é de $5. Qual o impacto de a aposta no flop ser igual ao ante em vez de ser o dobro do ante?
Supondo que o jogador seguisse a estratégia das regras convencionais de Las Vegas, onde o jogador ganha a aposta inicial com uma sequência ou uma mão melhor, a vantagem da casa aumentaria de 2,04% para 3,51%. Tenho certeza de que isso poderia ser reduzido com mudanças estratégicas específicas para cada regra. No entanto, meu computador leva 71 dias para analisar este jogo, então peço desculpas se encerrar minha resposta aqui.
Tive uma dúvida que surgiu durante um torneio em casa na outra noite. O jogador com mais fichas foi all-in e o jogador com menos fichas deu call. O jogador com menos fichas mostrou um par de ases enquanto estávamos juntando fichas. O jogador com mais fichas disse "você me venceu" e tentou descartar as cartas. Ele passou as cartas para o dealer para que ele as entregasse. Um jogador pode desistir da mão nesse momento se optar por descartar as cartas? Outro jogador na mão disse que não podia desistir, então continuamos a rodada. Ele acertou uma sequência de cartas para um flush, mas eu considerei a mão encerrada, já que ele disse verbalmente "estou perdendo" e passou as cartas para o dealer com a face para baixo. Acredito que se as cartas dele tocaram a pilha de descarte, elas estão mortas, mas ele pode desistir nesse momento por vontade própria? O jogador com mais fichas não era muito experiente e achou que estava perdendo. Agradeceria muito se você pudesse esclarecer isso para nós.
Para os detalhes das regras do pôquer, recorri ao meu amigo Jason. Eis o que ele disse: "Isso é muito interessante. Sempre que duas cartas são descartadas, a mão é considerada morta, sem exceção. No entanto, como se tratava de uma situação de all-in, isso não deveria ter acontecido. Em um torneio, quando alguém está all-in, todas as mãos devem ser reveladas. Se dois dos jogadores não estiverem all-in, o jogo continua sem que todas as mãos sejam expostas. Na minha opinião, a mão está morta, já que ele descartou as cartas. Não entendo por que ele faria isso! Espero que isso ajude um pouco."
Estive recentemente em Las Vegas e joguei um jogo novo para mim: World Poker Tour: All in Poker . Não usei os bônus e segui suas dicas de como jogar. Apostei US$ 15 no blind, então, em média, minhas apostas totais foram de aproximadamente US$ 100. Em um cassino, fui classificado como um jogador de US$ 15 e em outro, como um jogador de US$ 45. Não entendo por que dois cassinos, ambos do mesmo grupo empresarial, me deram duas classificações diferentes para as mesmas apostas no mesmo jogo, e também não entendo por que não fui classificado como um jogador de 90 a 100.
O primeiro cassino estava corretamente baseando o tamanho da sua aposta apenas no valor inicial (ante). O segundo estava contabilizando os aumentos (raises). Se o segundo cassino inclui os aumentos no cálculo da aposta média, então deveria usar uma vantagem da casa menor para fins de classificação. Na minha opinião, muitos cassinos não concedem benefícios aos jogadores de forma precisa. Cada cassino tem suas próprias políticas, independentemente do grupo empresarial ao qual pertence. O importante no seu caso é qual cassino lhe oferece o maior retorno pelo seu jogo. Há muitos fatores que influenciam essa decisão, além do tamanho médio da aposta.
Excelente site! Imperdível para novatos em Las Vegas e para quem pensa em ficar rico com jogos de azar. Existe uma proporção ideal entre a aposta inicial (ante) e a aposta bônus no jogo de mesa Texas Hold'em Bonus? Seria simplesmente 10% de bônus para a aposta inicial, já que você calculou que 90,4% das apostas bônus são perdedoras?
Obrigado pelas palavras gentis. Essa é uma pergunta que me fazem com frequência em relação a jogos com duas ou mais apostas. Você deve apostar 100% na aposta mais vantajosa. No caso do Texas Hold'em Bonus, o risco na aposta inicial (ante) é de 0,53% e na aposta bônus é de 8,54%, considerando as regras de Las Vegas para ambos os casos. Para comparar uma aposta com outra, acredito que o fator de risco deva ser considerado. Portanto, nesse caso, a proporção entre a aposta inicial e a aposta bônus deve ser infinita, já que a aposta bônus deve ser zero. O mesmo se aplica ao Three Card Poker, que geralmente é o jogo sobre o qual essa pergunta é feita. Nesse jogo, você deve apostar 100% na aposta inicial e 0% no Pairplus.
Tenho uma pergunta muito complexa que dividiu a minha opinião com a de um amigo. Em uma partida de Texas Hold'em com três jogadores, dois têm K/3 de naipes diferentes e um tem K/2 de naipes diferentes. Antes do flop, qual é a mão mais forte: K/2 ou K/3?
A situação com K/2 é muito melhor, porque os jogadores com K/3 podem ter que dividir o pote. Como mostra minha calculadora de Texas Hold'em para três a cinco jogadores , o jogador com K/2 pode esperar ganhar 42,96% do pote, e cada jogador com K/3, 28,52%.
Comecei a jogar Texas Hold'em sem limite recentemente. Minha dúvida é a seguinte: depois que os blinds (big blind e small blind) são pagos e todos dão check ou call, e então vem o flop, qual é a aposta mínima que deve ser feita? Ela precisa ser pelo menos igual ao big blind, ou pode ser de qualquer valor (inclusive menor que o big blind)? A aposta muda depois do turn e do river?
Em um jogo sem limite, a aposta mínima é igual ao valor do big blind. Isso é válido antes e depois do flop.
Olá, todo-poderoso Mago. Meus amigos e eu fizemos uma aposta sobre Texas Hold'em. Eles disseram que 7/2 é sempre a pior mão que você pode ter, não importa o que seu oponente tenha. Mas eu disse que 6/2 teria menos chances de ganhar contra 7/2 pré-flop. Quem está certo?
Se um jogador com 7/2 de naipes diferentes enfrentasse um jogador com 6/2 de naipes diferentes, os possíveis resultados seriam os seguintes, de acordo com minha calculadora de Texas Hold 'Em .
7/2 vitórias: 57,07%
6/2 vitórias: 25,13%
Empate: 17,80%
No entanto, isso não prova que 7/2 seja a melhor mão em geral. Considerando apenas a sua própria mão, de acordo com minhas várias tabelas de classificação de poder, 7/2 de naipes diferentes é pior que 6/2 de naipes diferentes. Para quatro jogadores ou menos, a pior mão é 3/2 de naipes diferentes.
Portanto, se a aposta fosse formulada como quem venceria entre 6/2 e 7/2 offsuit, você ganharia. No entanto, isso não prova que 7/2 seja a melhor mão em geral, apenas para essa situação específica.
Olá! Ótimo site! Espero que você possa responder a mais uma pergunta bônus sobre Texas Hold'em, já que existe uma variação diferente onde eu jogo, no Colorado. Ao contrário das regras de Las Vegas e Atlantic City, no Colorado todas as apostas devem ser iguais a US$ 5 (o mínimo da mesa é igual ao limite de aposta de US$ 5 imposto pela lei do Colorado), então a aposta no flop deve ser igual (e não o dobro) da aposta inicial. De resto, as regras do jogo parecem corresponder à versão de Las Vegas que você analisou.
Obrigado. Normalmente, a vantagem da casa no Texas Hold 'Em Bonus é de 2,04% pelas regras de Las Vegas e de 5,59% pelas regras de Atlantic City. Você está certo ao afirmar que nenhuma aposta individual pode ultrapassar US$ 5 no Colorado. De acordo com a versão das regras do Colorado que você descreveu acima, a vantagem da casa é de 2,35%.
Já ouvi em jogos de pôquer o termo "estrangular o cego" ou algo parecido. O que significa isso?
Perguntei ao meu amigo Jason sobre isso. Eis o que ele disse:
"Acho que o que ela quis dizer é um blind straddle. Isso significa que a pessoa que age depois do big blind aumenta para o dobro do big blind, antes de olhar suas cartas. Geralmente, isso é feito para estimular a ação em uma mesa onde os potes estão pequenos e há muitos folds pré-flop. Digamos que seja um jogo de limit hold'em de $6-$12, com o small blind de $3 e o big blind de $6. Estou na posição seguinte ao big blind e faço um straddle, aumentando para $12 antes de olhar minhas cartas." — Jason
Estava jogando em uma liga de pôquer uma noite e essa situação aconteceu. Os blinds eram de $300/$600 e o primeiro jogador a agir apostou $2.000, e os dois seguintes desistiram quando chegou a minha vez. Como não vi a aposta inicial, apostei $3.000 sem dizer se ia aumentar ou pagar, já que achei que tinha sido o primeiro a apostar. Comecei a retirar $1.000 para pagar, mas me disseram que minhas fichas tinham que permanecer na mesa e que eu teria que colocar mais $1.000 para aumentar a primeira aposta ou simplesmente desistir da mão. Poderiam me dar a regra correta para essa situação? Obrigado.
Acho que nenhum de vocês está certo. É correto afirmar que, ao apostar mais de US$ 2.000, você estava insinuando que aumentaria o pote. O aumento mínimo deveria ter sido de US$ 1.400, totalizando uma aposta de US$ 3.400, contrariando as regras da mesa. Isso porque a última aposta de US$ 2.000 foi um call de US$ 600 e um aumento de US$ 1.400. Sua aposta foi de apenas US$ 1.000. Portanto, você precisava apostar mais US$ 400 ou desistir da mão. ( fonte )
Você acha que jogadores que ganham algo em um torneio de poker ao vivo devem dar uma gorjeta adicional se compraram um "add-on do dealer" no início do torneio? Eu jogo em muitos torneios com buy-in baixo que usam esses add-ons, e os vencedores são sempre lembrados de que "gorjetas são muito apreciadas". Me parece que eu já dou gorjeta, mesmo nos torneios em que não ganho prêmios, e dar gorjeta adicional só reduz a pequena vantagem que eu possa ter em uma modalidade de jogo que já é difícil de vencer (devido à "comissão", formatos que diminuem a importância da habilidade, etc.). Por outro lado, não quero parecer mesquinho. O que você sugere?
Como não jogo muito pôquer, precisei perguntar a David Matthews o que é um "adicional do dealer". Eis o que ele disse.
A taxa adicional do dealer é uma taxa extra e opcional que você paga no momento da inscrição. Esse valor é destinado exclusivamente aos dealers como forma de compensá-los pelo tempo dedicado a distribuir as cartas no torneio. Normalmente, você recebe um número adicional de fichas iniciais, por exemplo, 2500 em vez de 2000.Concordo com o Dave. Gostaria de acrescentar que também me oponho à prática de extorquir jogadores em torneios com taxas opcionais, como recompras e compra de curingas, a menos que esses valores sejam de alguma forma devolvidos aos jogadores, o que geralmente não acontece. Se o torneio não for lucrativo para o cassino, por favor, abandonem as pretensões e façam os jogadores pagarem mais antecipadamente para participar.Dar gorjeta, independentemente de comprar o complemento ou não, deveria ser sempre opcional. Se eu tivesse comprado o complemento, estaria menos inclinado a dar gorjeta. Aliás, eu sempre compro o complemento. Não sei se é matematicamente correto do ponto de vista do valor esperado, mas parece ser a coisa certa a fazer se vou participar do torneio.
Se não houvesse acréscimo para o dealer, eu acho apropriado que os vencedores deem gorjeta aos dealers. Se fosse obrigado a dizer, eu sugeriria de 1% a 2% do prêmio, e quanto menor o prêmio, maior a porcentagem. Na situação em questão, eu reduziria a gorjeta pelo produto do valor total do acréscimo para o dealer e a proporção do meu prêmio em relação ao prêmio total. Se isso resultar em gorjeta zero ou negativa, então você tem um dilema. Eu provavelmente faria como faço quando os restaurantes exigem uma gorjeta obrigatória de 18% a 20%: deixaria apenas um pequeno valor simbólico para manter as aparências.
Por que sua tabela de classificação de mãos difere daquela de David Sklansky (publicada em seu livro "Hold 'Em Poker for Advanced Players" , que também aparece na entrada da Wikipédia sobremãos iniciais de Texas Hold'em )? Por exemplo, Sklansky classifica 76 suited e A9 offsuit igualmente, com uma classificação de 5. Sua tabela classifica 76 suited como "11", mas classifica A9 suited como "16"! Poderia explicar por que existem essas discrepâncias?
Acho que você interpretou mal a tabela do Skanskey. Ele classifica 7-6 suited como equivalente a A-9 offsuited, com nota 5. Eu classifico 7-6 suited com nota 11 e A-9 offsuited com nota 10. Portanto, ambos os classificamos de forma semelhante.
No cassino Buffalo Thunder em Santa Fé, Novo México, existe uma aposta paralela progressiva no Ultimate Texas Hold 'Em que eu nunca vi antes. Você tem alguma ideia das probabilidades?
Obrigado pela informação. Abordo esse assunto na minha página sobre Ultimate Texas Hold 'Em .
Você acha que jogadores que ganham prêmios em torneios de poker ao vivo devem dar uma gorjeta adicional se compraram o add-on "dealer's add-on" no início do torneio? Eu jogo em muitos torneios com buy-in baixo que usam esses add-ons, e os vencedores são sempre lembrados de que "gorjetas são muito apreciadas". Me parece que eu já dei gorjeta, mesmo nos torneios em que não ganho prêmios, e dar gorjeta adicional só reduz a pequena vantagem que eu possa ter em uma modalidade de jogo que já é difícil de vencer (devido à "comissão", formatos que diminuem a importância da habilidade, etc.). Por outro lado, não quero parecer mesquinho. O que você sugere?
Para benefício de outros leitores, um "adicional do dealer" é uma compra opcional de fichas adicionais em um torneio de pôquer. Normalmente, o custo por ficha do adicional do dealer é menor do que a taxa de inscrição original, sendo, portanto, uma boa opção. Respondendo à sua pergunta, acredito que você tem todo o direito de reduzir a gorjeta caso esteja entre os premiados, independentemente de ter comprado ou não o adicional do dealer. É como dar gorjeta em um restaurante, onde já há uma taxa de serviço de 18%. Uma gorjeta apropriada para o vencedor, na minha opinião, é o valor que os dealers teriam recebido se estivessem trabalhando em jogos a dinheiro durante o torneio, menos o valor que receberam do adicional do dealer.
Gostaria de aproveitar esta oportunidade para declarar que me oponho a quaisquer custos adicionais em torneios, a menos que o dinheiro extra pago seja destinado ao prêmio total, o que geralmente não acontece. Os torneios costumam ser estruturados de forma que o pagamento das taxas adicionais represente um bom custo-benefício, por isso a maioria dos jogadores exerce esse direito, inclusive eu. Suas chances de ganhar diminuem significativamente se você não pagar. No entanto, se todos os jogadores pagam as taxas adicionais, então deveriam abandonar as pretensões e simplesmente cobrar um valor maior pelo torneio desde o início.
Não entendo como é possível que nas suas tabelas de poder do Texas Hold'em, o A-7 tenha uma classificação inferior ao KJ suited, mas na sua calculadora o A7 tenha uma probabilidade maior de ganhar.
Boa pergunta. Para benefício de outros leitores, aqui estão as probabilidades contra uma mão aleatória com cada uma dessas duas mãos iniciais em um jogo de dois jogadores:
KJ de terno vs. A-7 sem terno
| Mão | Ganhar | Perder | Empate | Valor Esperado |
K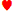 J J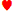 | 0,6148 | 0,3634 | 0,0218 | 0,2513 |
UM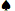 7 7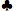 | 0,5717 | 0,3949 | 0,0334 | 0,1768 |
No entanto, de acordo com minha calculadora de Texas Hold'em para dois jogadores, as probabilidades dessas duas mãos se enfrentarem são:
A7 vence = 53,52%
Vitórias de KJ = 46,10%
Empate = 0,39%
Então, o Rei Valete de naipe único está classificado mais alto na minha tabela, mas é inferior ao Ás 7 de naipe único em um confronto direto. Por quê?
A resposta é difícil de explicar. Com duas mãos se enfrentando, é preciso considerar como elas interagem entre si. Por exemplo, na tabela de força inicial das mãos, AK fora do naipe é apenas ligeiramente melhor que AQ fora do naipe, com valores esperados de 0,3064 e 0,2886, respectivamente. No entanto, se as compararmos diretamente, o AK supera o AQ, como segue:
AK vence 71,72%
AQ vence = 23,69%
Empate = 4,58%
No jogo A7 offsuit contra KJ suited, o ás é muito superior ao rei e ao valete. A maior chance de vitória do jogador com KJ ocorre se ele formar um par com o rei ou o valete e nenhum ás aparecer. Demonstro que a probabilidade disso é de apenas 37,73%. Os 46,10% restantes da probabilidade de vitória do KJ vêm de mãos mais fortes.
Embora A7 seja forte contra KJ, é mais frequentemente dominado do que KJ por mãos aleatórias.
Talvez seja uma comparação inadequada, mas é semelhante ao jogo pedra, papel e tesoura . Entre jogadores habilidosos, individualmente, cada lançamento deveria ter aproximadamente a mesma força. No entanto, se um jogador joga papel e o outro tesoura, a força não importa, e a tesoura vencerá.
Gostaria de saber sua opinião sobre uma discussão acalorada que presenciei no poker do Wynn. Aqui está um resumo: um jogador fez um all-in e empurrou todas as suas fichas para o pote. Outro jogador também fez o mesmo e perdeu. O dealer começou a contar as fichas, que incluíam duas fichas pretas de $100 escondidas em meio a várias fichas azuis de $1 e vermelhas de $5. Descobriu-se que o primeiro jogador as tinha no fundo de suas pilhas de fichas azuis e vermelhas. O segundo jogador argumentou que não teria feito o all-in se soubesse das fichas pretas. O Wynn decidiu a favor do primeiro jogador, mas ele ficou furioso. O Wynn tomou a decisão correta?
Não sou especialista nos detalhes das regras do pôquer, então recorri a David Matthews para me ajudar com isso. Aqui está o que ele disse:
Jogo bastante poker, principalmente NL 2-5 e NL 5-10. A regra é que as fichas maiores devem estar visíveis na frente ou por cima, e se o dealer soubesse da existência de fichas pretas, deveria ter solicitado que fossem exibidas. O problema é que, se as fichas estiverem escondidas, como o dealer vai vê-las? As pilhas também devem ser de uma única denominação. Uma pilha de fichas vermelhas (US$ 5) sobre uma ficha de US$ 1 é considerada uma pilha suja, porque se alguém fosse olhar para a pilha, provavelmente chutaria o valor errado. Nesse caso, a diferença seria de apenas US$ 4, mas é assim que funciona. Curiosamente, uma pilha de fichas vermelhas com uma ficha de US$ 1 por cima não é considerada uma pilha suja. Acho que as regras sobre pilhas sujas são um pouco complicadas demais.A visibilidade das fichas é um problema real no No-Limit Hold'em, pois, como demonstrado nesta situação, pode haver confusão. Infelizmente, a decisão da equipe de poker do Wynn foi correta, mas foi realmente uma pena para a pessoa com a mão perdedora.
Já passei por uma situação parecida que me custou 600 dólares. Apostei tudo num blefe contra um cara que tinha um monte de fichas e algumas notas. Notas de 100 dólares são comuns na maioria dos cassinos da cidade. Eu perguntei: "Quanto você tem? Duas notas?". Ele só assentiu e não disse nada. Apostei tudo. Ele pagou na hora com três reis. Na verdade, ele tinha oito notas, e a casa me obrigou a pagar. Eu não teria tentado o blefe para um all-in se soubesse quanto dinheiro ele tinha. Foi caro.
É por isso que SEMPRE pergunto em all-ins. Mesmo que um cara tenha 5 fichas vermelhas (US$ 25) e aposte tudo, eu pergunto ao crupiê quanto é. Os crupiês às vezes ficam irritados e me olham como se dissessem: "É bem óbvio, não é?". Além disso, os jogadores também me dão trabalho às vezes. Eles me dizem que obviamente são US$ 100 ou algo parecido. Não importa. Eu pergunto: "Quanto é?" repetidamente.
Outra coisa é que geralmente aposto um valor em vez de dizer "tudo ou nada". Se eu tivesse apostado 500 dólares contra o cara com os três reis, não importaria quantas notas ou fichas ele tivesse. Eu só teria que pagar os 500 dólares.
Pessoalmente, sou contra o uso de notas na mesa, porque tenho que ficar perguntando o tempo todo quantas notas as pessoas têm. Elas se ofendem quando você pergunta isso várias vezes, principalmente quando têm menos dinheiro na mesa do que os outros jogadores, porque ficam constrangidas de dizer "duas notas". E aí, em todas as mãos que jogo com elas, tenho que perguntar de novo, porque nunca se sabe se elas adicionaram mais notas à pilha entre as mãos. Ou se ganharam uma mão que você não viu. Além disso, o simples fato de você perguntar quanto dinheiro a alguém tem pode revelar informações sobre a sua mão.
Acho que fichas de papel não deveriam ser usadas, e em jogos de 2 a 5 jogadores ou menos, o máximo de fichas permitidas deveria ser de 100 dólares. Mas essa não é uma opinião popular.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
O que deve acontecer em um jogo de pôquer se um jogador morrer no meio da mão?
Perguntei a um ex-regulador de jogos e presidente de cassino de Nevada sobre isso. Ele disse que seria tratado como uma situação de "tudo ou nada", da mesma forma que uma desconexão acidental é tratada no pôquer online.
Em outras palavras, um pote paralelo seria formado com as fichas que estavam no centro da mesa no momento da morte. Quaisquer apostas adicionais seriam então separadas em um pote à parte. Se o jogador falecido tivesse a melhor mão, ele ganharia o pote paralelo. Independentemente de ganhar ou perder, quaisquer fichas que ele tivesse na mesa após a mão seriam destinadas ao espólio do falecido.
Essa questão foi levantada e discutida no meu fórum, Wizard of Vegas .
Qual mão inicial tem a maior probabilidade de vencer um par de ases aleatórios em um jogo de Texas Hold 'Em para dois jogadores?
Usando minha calculadora de Texas Hold'em , mostro que a resposta é 5-6 do mesmo naipe. Se o 5-6 for de um naipe diferente dos dois ases, a probabilidade de vitória é de 22,87% e a de empate, 0,37%. Se o 5-6 for do mesmo naipe de um dos ases, a probabilidade de vitória é de 21,71% e a de empate, 0,46%. Em média, o jogador com 5-6 do mesmo naipe perderá 0,55005 unidades, supondo que aposte uma unidade, e terá uma chance de vitória, caso haja um vencedor, de 22,383%.


