Programas de jogos de TV - Perguntas frequentes
Não é exatamente um jogo de azar, mas sempre me perguntei, no programa "The Price is Right", qual a melhor estratégia para girar a roda gigante quando você não é o último a girar. Supondo que você não possa controlar o giro (resultado completamente aleatório), com incrementos de 5 centavos, de US$ 0,05 a US$ 1,00, você tem direito a um giro ou a dois giros somados, e não pode ultrapassar US$ 1,00. Qual seria o valor mínimo para não girar a roda pela segunda vez, de forma a ter a melhor chance de vencer o jogador que girar depois de você?
O primeiro jogador deve girar a roleta novamente se o seu primeiro giro resultar em 65 centavos ou menos.
Se alguma das seguintes condições for verdadeira, o segundo jogador deve girar a roleta novamente.
- A pontuação dele é menor que a pontuação do primeiro jogador.
- Sua pontuação é de 50 centavos ou menos.
- Sua pontuação é de 65 centavos ou menos e ele empatou com o primeiro jogador.
Qual é a estratégia ideal para o jogo Plinko no programa "The Price is Right"?
Da esquerda para a direita, os prêmios são: $100, $500, $1000, $0, $10000, $0, $1000, $500 e $100. Eu precisaria saber a configuração exata dos pinos no tabuleiro para fazer uma análise perfeita, mas, apenas observando o tabuleiro (veja o link acima), acredito fortemente que o jogador deva soltar o disco diretamente sobre o prêmio de $10.000. Embora esteja cercado por dois zeros, todos os outros prêmios são insignificantes em comparação com o prêmio principal. Portanto, a estratégia do jogador deve ser maximizar a probabilidade de ganhar o prêmio principal, soltando o disco diretamente acima dele. Para confirmar ou refutar minha hipótese, fiz uma pesquisa e encontrei muitos links dedicados ao estudo deste jogo. Este ( www.amstat.org/publications/jse/v9n3/biesterfeld.html ) é um dos melhores e concorda com minha conclusão. O texto afirma, em parte, que o valor esperado de soltar o disco no meio é de US$ 2.557,91, em cada lado do meio é de US$ 2.265,92, e diminui à medida que se afasta do centro.
No programa de jogos Let's Make a Deal, há três portas. Digamos, por exemplo, que duas portas revelam uma cabra e uma revela um carro novo. O apresentador, Monty Hall, escolhe dois participantes para escolherem uma porta. Toda vez que Monty abre primeiro uma porta que revela uma cabra, digamos que desta vez a porta era do primeiro participante. Embora Monty nunca tenha feito isso, e se ele oferecesse ao outro participante a chance de trocar de porta, para a outra porta que ainda não foi aberta? Ele deveria trocar?
Sim! A chave para este problema é que o apresentador está predestinado a abrir uma porta com um bode. Ele sabe qual porta tem o carro, então, independentemente das portas escolhidas pelos jogadores, ele sempre pode revelar um bode primeiro. A questão é conhecida como o "Paradoxo de Monty Hall". Grande parte da confusão em torno dela se deve ao fato de que, frequentemente, quando a questão é formulada, não fica claro que o apresentador sabe onde está o carro e sempre revela um bode primeiro. Acho que parte da culpa recai sobre Marilyn Vos Savant , que formulou a questão de forma inadequada em sua coluna. Vamos supor que o prêmio esteja atrás da porta 1. A seguir, vejamos o que aconteceria se o jogador (o segundo participante) tivesse a estratégia de não trocar de porta.
- Jogador escolhe a porta 1 --> jogador ganha
- Jogador escolhe a porta 2 --> jogador perde
- Jogador escolhe a porta 3 --> jogador perde
A seguir, veja o que aconteceria se o jogador adotasse uma estratégia de troca de personagens.
- O jogador escolhe a porta 1 --> O anfitrião revela a cabra atrás da porta 2 ou 3 --> O jogador troca para a outra porta --> O jogador perde
- O jogador escolhe a porta 2 --> o apresentador revela a cabra atrás da porta 3 --> o jogador troca para a porta 1 --> o jogador vence
- O jogador escolhe a porta 3 --> O apresentador revela a cabra atrás da porta 2 --> O jogador troca para a porta 1 --> O jogador vence
Portanto, ao não trocar de arma, o jogador tem 1/3 de chance de ganhar. Ao trocar de arma, o jogador tem 2/3 de chance de ganhar. Logo, o jogador definitivamente deveria trocar de arma.
Para saber mais sobre o paradoxo de Monty Hall, recomendo o artigo na Wikipédia .
Minha pergunta é sobre um problema conhecido como o "paradoxo dos dois envelopes". Você está em um programa de jogos. À sua frente, há dois envelopes, cada um contendo uma quantia desconhecida de dinheiro. É informado que um dos envelopes contém o dobro do dinheiro do outro. Você precisa escolher um envelope. Você escolhe um. Ele contém US$ 50.000. Agora, você é informado de que pode ficar com o envelope escolhido ou trocá-lo pelo outro. Você deve trocar? Sabendo de antemão que poderia trocar, não importa, pois você simplesmente escolheria o envelope que deseja. Mas, como você só descobre a possibilidade de troca depois de escolher um envelope, a escolha inicial e a opção de troca são dois eventos independentes, correto? Dito isso, ao decidir trocar ou não, o outro envelope contém o dobro ou a metade do que você tem atualmente. Portanto, ele contém US$ 100.000 ou US$ 25.000. Como há 50% de chance de qualquer um dos dois ocorrer, o valor esperado do outro envelope é de US$ 62.500. De forma geral, se considerarmos x como o valor que você selecionou originalmente, então o valor esperado (VE) do outro envelope é 1,25x. Portanto, a troca é sempre correta. Isso está correto? Obrigado.
Conheço bem esse problema. Abordo-o no meu site de problemas de matemática , problema número 6. Lá, trato do caso geral, inclusive ignorando o conteúdo do primeiro envelope. No entanto, para responder à sua pergunta, não podemos ignorar o contexto em que o jogo está sendo realizado. Você disse que era um "programa de jogos". Na maioria dos programas de jogos, US$ 50.000 é um bom prêmio. Poucos participantes do "The Price is Right" chegam a esse valor. Eu diria que menos de 50% dos jogadores do "Who Wants to be a Millionaire" atingem esse patamar. Enquanto isso, prêmios de US$ 25.000 não são incomuns em programas de jogos. Carros são ganhos rotineiramente no "The Price is Right", com valores em torno de US$ 25.000. O nível de US$ 32.000 é um prêmio comum no "Who Wants to be a Millionaire". O prêmio médio por episódio no "Jeopardy!" é de aproximadamente US$ 25.000. O grande Ken Jennings teve uma média de apenas US$ 34.091 em suas 74 vitórias. Então, o que quero dizer é que US$ 50.000 é um bom prêmio para um programa de jogos, e prêmios de US$ 100.000 são muito menos comuns do que os de US$ 25.000. Portanto, como um conhecedor de programas de jogos, na minha opinião, é mais provável que o outro envelope contenha US$ 25.000 do que US$ 100.000. Então, no seu exemplo, eu diria que é melhor ficar com os US$ 50.000. Isso também mostra que você nunca pode presumir que as chances de o outro envelope ter metade ou o dobro do prêmio sejam exatamente de 50/50. Depois de ver o valor e considerá-lo no contexto do local onde o jogo está sendo realizado, você pode tomar uma decisão inteligente sobre a troca, o que invalida o argumento de 1,25x.
Minha pergunta diz respeito ao programa de jogos "Deal or No Deal", muito popular na Austrália e que em breve chegará à Inglaterra. O participante visualiza vinte e seis maletas numeradas, cada uma contendo uma quantia oculta de dinheiro, variando de 50 centavos a 200.000 dólares, conforme abaixo.
- $ 0,50
- $ 1
- $ 2
- $ 5
- $ 10
- $ 25
- $ 50
- $ 75
- $ 100
- $ 150
- $ 250
- $ 500
- $ 750
- $ 1.000
- $ 1.500
- $ 2.000
- $ 3.000
- $ 5.000
- $ 7.500
- US$ 10.000
- $ 15.000
- $ 30.000
- $ 50.000
- $ 75.000
- $ 100.000
- US$ 200.000
O participante escolhe uma das maletas para ser SUA maleta. Através de um processo de eliminação, abrindo as outras maletas, ele tenta descobrir quanto dinheiro sua maleta tem ou se seria mais sensato aceitar uma "Oferta do Banco". As Ofertas do Banco são baseadas na média aritmética das maletas restantes, mas não são equivalentes a ela. Portanto, se restarem principalmente maletas de alto valor, há uma grande chance de a maleta do participante ser valiosa e, consequentemente, a Oferta do Banco será generosa. Por outro lado, se o jogador tiver menos sorte e tiver aberto as maletas mais valiosas, a Oferta do Banco será baixa. Qual seria a melhor estratégia a ser usada se você fosse um participante deste jogo? Uma estratégia intuitiva, sem base matemática, seria ignorar as Ofertas do Banco e continuar abrindo maletas até que a maleta de US$ 200.000 fosse aberta e eliminada, ou até que as maletas de US$ 100.000 e US$ 75.000 fossem abertas e eliminadas. Qual é a matemática por trás deste jogo, Mago?
O programa "Deal or No Deal" acaba de estrear aqui nos EUA. As regras parecem as mesmas, exceto que nossos prêmios chegam a um milhão de dólares, conforme descrito a seguir.
- 0,01
- 1
- 5
- 10
- 25
- 50
- 75
- 100
- 200
- 300
- 400
- 500
- 750
- 1000
- 5000
- 10000
- 25000
- 50000
- 75000
- 100000
- 200000
- 300000
- 400000
- 500000
- 750000
- 1000000
Eis o fluxo do jogo:
- O jogador escolhe um caso para si.
- O jogador abre seis das 25 caixas restantes.
- O banqueiro faz uma oferta.
- Caso o jogador recuse, ele abrirá mais cinco dos 19 casos restantes.
- O banqueiro faz uma oferta.
- Caso o jogador recuse, ele abrirá mais quatro dos 14 casos restantes.
- O banqueiro faz uma oferta.
- Caso o jogador recuse, ele abrirá mais três dos 10 casos restantes.
- O banqueiro faz uma oferta.
- Caso o jogador recuse, ele abrirá mais duas das 7 caixas restantes.
- O banqueiro faz uma oferta.
- Se o jogador recusar, ele abre mais um dos casos restantes.
- Continue repetindo os passos 11 e 12 até que o jogador aceite uma oferta ou fique com a última caixa fechada.
O gráfico a seguir mostra o valor esperado do jogador e a oferta do banqueiro.
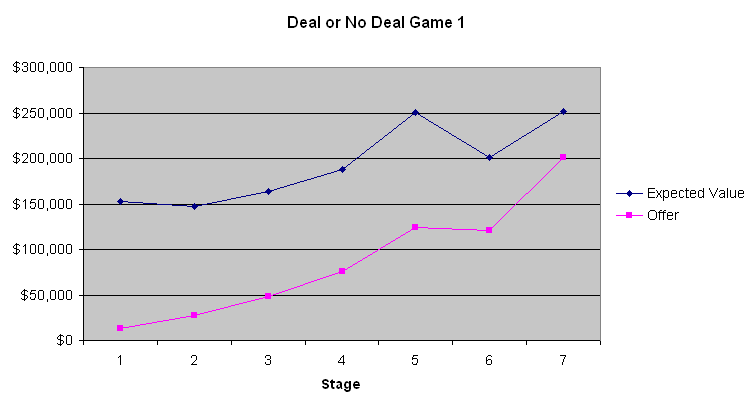
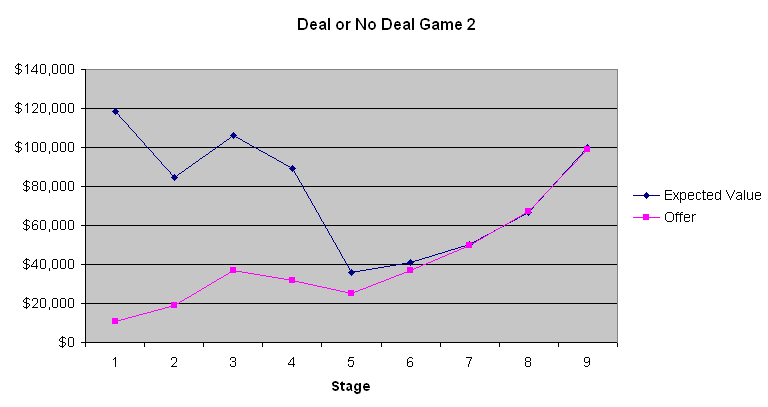
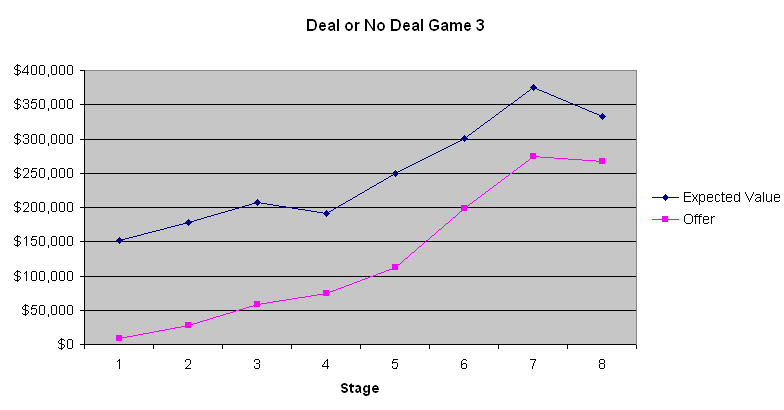
A conclusão mais óbvia a se tirar desses três gráficos é que as primeiras quatro a seis ofertas do banco são péssimas. A mala média contém US$ 131.477,54 antes mesmo de ser aberta. Oferecer apenas de US$ 9.000 a US$ 13.000 na primeira etapa é um negócio que só um tolo aceitaria. No entanto, gradualmente, as ofertas melhoram. O Jogo 2 mostra que os valores esperados eram quase os mesmos que as ofertas do banqueiro no final do jogo, quando o valor esperado do jogador era relativamente baixo. Contudo, nos Jogos 1 e 3, quando os valores esperados eram maiores, o banqueiro aparentemente estava tentando se aproveitar da aversão ao risco da maioria das pessoas quando grandes quantias estão envolvidas. Não sei se isso fez diferença, mas o participante do Jogo 2 parecia ser um apostador que queria ganhar muito. Com base nos comentários do apresentador, que se comunica com o banqueiro por telefone, o banqueiro parece levar em consideração as palavras e ações dos participantes. Se eu estivesse no lugar do banqueiro, agiria de forma muito parecida.
Se o jogador não for avesso nem propenso ao risco, e ignorando as implicações fiscais, deve continuar recusando as ofertas do banqueiro até que uma delas supere a média das malas restantes. Para a maioria das pessoas, a natureza progressiva do código tributário favorece a aceitação de um acordo. Como já mencionei, diria que o valor do dinheiro é proporcional ao logaritmo do montante. Portanto, quanto mais riqueza você tiver ao iniciar o jogo, mais inclinado você deve estar a arriscar e recusar as ofertas do banqueiro. Com quantias tão elevadas envolvidas, nenhuma estratégia será adequada para todos. No entanto, posso afirmar com bastante segurança que o jogador deve recusar as primeiras quatro a seis ofertas e, em seguida, aceitar as ofertas caso a caso (trocadilho intencional).
Links:
Você pode assistir ao programa Deal or No Deal no site da NBC.
Arquivo de programas anteriores.
Estou assistindo ao programa "Deal or No Deal". Percebi que a "oferta" do banqueiro é simplesmente o valor restante das caixas dividido pelo número de caixas (com arredondamentos). Existe alguma estratégia nesse jogo, ou aceitar o acordo é sempre uma opção aceitável? Depende de quantas caixas você precisa abrir ou de algum outro fator?
Como mostrei na minha coluna de 26 de dezembro de 2005, a oferta do banqueiro geralmente é muito menor do que a média dos demais casos. No entanto, hipoteticamente, se fosse sempre assim, todas as estratégias teriam o mesmo valor esperado. O jogador seria indiferente a todas as ofertas.
No início do programa "Deal or No Deal", a probabilidade de escolher a maleta de 1.000.000 de dólares é de 1 em 26. Depois de eliminar todas as maletas, exceto uma, qual é a probabilidade de a minha maleta conter o prêmio de um milhão de dólares? É de 50/50 ou continua sendo de 1 em 26?
50-50
Em sua coluna de 5 de abril de 2006, você afirma que, se restarem apenas duas maletas no programa "Deal or No Deal" e o prêmio de um milhão de dólares ainda estiver em jogo, a probabilidade de a minha maleta ganhar o milhão é de 50%. Discordo. Isso não seria apenas uma variação do problema de Monty Hall? Ou seja, o milhão tem mais probabilidade de estar no palco do que na maleta dele?
Não. Muita gente está discutindo comigo sobre isso. Muitos autores afirmam que as probabilidades não mudam se novas informações forem introduzidas. Então, se a probabilidade começa em 1 em 26, ela deve permanecer assim. Ao contrário do que dizem os vendedores de sistemas de apostas, as probabilidades podem, sim, mudar conforme novas informações são introduzidas. Não quero tentar ensinar probabilidade básica aqui, mas qualquer livro de matemática de nível universitário sobre probabilidade condicional ou o Teorema de Bayes deve abordar esse tópico muito bem.
Deixe-me explicar o que acontecia no programa "Let's Make a Deal". O participante escolhia uma entre três cortinas. Uma continha um prêmio muito valioso e as outras duas, prêmios menores. Para fins de argumentação, digamos que atrás de uma cortina havia um carro e atrás das outras duas, uma cabra. Então, Monty sempre, repito, SEMPRE, abria uma das duas cortinas não escolhidas para revelar uma cabra. Depois de centenas de programas, isso implicaria que Monty Hall (o apresentador) sabia onde estava o carro e abria deliberadamente uma cortina que revelava uma cabra. Obviamente, quando o jogador escolhia sua cortina, a probabilidade de ela conter o carro era de 1/3 e a probabilidade de uma das duas cortinas não escolhidas conter o carro era de 2/3. Monty, então, estava predestinado a abrir uma cortina não escolhida que continha um prêmio. Predestinado é a palavra-chave aqui. Como Monty não podia abrir a cortina do jogador nessa etapa, a probabilidade de a cortina do jogador revelar o carro permanecia em 1/3. A probabilidade de uma cortina não escolhida revelar o carro permanece em 2/3, porém agora está toda concentrada em uma única cortina. Portanto, após a revelação de um bode, a probabilidade de a cortina do jogador conter o carro é de 1/3 e a probabilidade de a outra cortina fechada conter o carro é de 2/3, tornando a troca uma escolha sábia.
A tabela a seguir mostra todos os resultados possíveis. No caso em que o jogador escolheu a cortina com o carro, eu fiz com que Monty abrisse uma cortina aleatoriamente. Você pode ver que não trocar resulta em uma probabilidade de 1/3 de ganhar, e trocar resulta em uma probabilidade de 2/3 de ganhar.
Vamos fazer um acordo
| Jogador Escolhe | Carro | Cortina Aberto | Probabilidade | Ganhe por Comutação |
| 1 | 1 | 1 | 0% | n / D |
| 1 | 1 | 2 | 5,56% | N |
| 1 | 1 | 3 | 5,56% | N |
| 1 | 2 | 1 | 0% | n / D |
| 1 | 2 | 2 | 0% | n / D |
| 1 | 2 | 3 | 11,11% | Y |
| 1 | 3 | 1 | 0% | n / D |
| 1 | 3 | 2 | 11,11% | Y |
| 1 | 3 | 3 | 0% | n / D |
| 2 | 1 | 1 | 0% | n / D |
| 2 | 1 | 2 | 0% | n / D |
| 2 | 1 | 3 | 11,11% | Y |
| 2 | 2 | 1 | 5,56% | N |
| 2 | 2 | 2 | 0% | n / D |
| 2 | 2 | 3 | 5,56% | N |
| 2 | 3 | 1 | 11,11% | Y |
| 2 | 3 | 2 | 0% | n / D |
| 2 | 3 | 3 | 0% | n / D |
| 3 | 1 | 1 | 0% | n / D |
| 3 | 1 | 2 | 11,11% | Y |
| 3 | 1 | 3 | 0% | n / D |
| 3 | 2 | 1 | 11,11% | Y |
| 3 | 2 | 2 | 0% | n / D |
| 3 | 2 | 3 | 0% | n / D |
| 3 | 3 | 1 | 5,56% | N |
| 3 | 3 | 2 | 5,56% | N |
| 3 | 3 | 3 | 0% | n / D |
Enquanto isso, em "Deal or No Deal", nada é predeterminado. Vamos supor que, em "Deal or No Deal", os valores restantes sejam de US$ 0,01, US$ 1 e US$ 1.000.000. Com três maletas restantes, É possível que a maleta aberta contenha o prêmio de um milhão de dólares. A tabela a seguir mostra os possíveis resultados com três maletas restantes. Lembre-se: o jogador não pode abrir sua própria maleta.
Acordo ou não acordo
| Jogador Escolhe | Milhões de dólares | Caso Aberto | Probabilidade | Ganhe por Comutação |
| 1 | 1 | 1 | 0% | n / D |
| 1 | 1 | 2 | 5,56% | N |
| 1 | 1 | 3 | 5,56% | N |
| 1 | 2 | 1 | 0% | n / D |
| 1 | 2 | 2 | 5,56% | Sem esperança |
| 1 | 2 | 3 | 5,56% | Y |
| 1 | 3 | 1 | 0% | n / D |
| 1 | 3 | 2 | 5,56% | Y |
| 1 | 3 | 3 | 5,56% | Sem esperança |
| 2 | 1 | 1 | 5,56% | Sem esperança |
| 2 | 1 | 2 | 0% | n / D |
| 2 | 1 | 3 | 5,56% | Y |
| 2 | 2 | 1 | 5,56% | N |
| 2 | 2 | 2 | 0% | n / D |
| 2 | 2 | 3 | 5,56% | N |
| 2 | 3 | 1 | 5,56% | Y |
| 2 | 3 | 2 | 0% | n / D |
| 2 | 3 | 3 | 5,56% | Sem esperança |
| 3 | 1 | 1 | 5,56% | Sem esperança |
| 3 | 1 | 2 | 5,56% | Y |
| 3 | 1 | 3 | 0% | n / D |
| 3 | 2 | 1 | 5,56% | Y |
| 3 | 2 | 2 | 5,56% | Sem esperança |
| 3 | 2 | 3 | 0% | n / D |
| 3 | 3 | 1 | 5,56% | N |
| 3 | 3 | 2 | 5,56% | N |
| 3 | 3 | 3 | 0% | n / D |
O que a tabela do Deal or No Deal mostra é que, com três caixas restantes, a probabilidade de o jogador abrir a caixa de um milhão de dólares é de 1/3 (sem chance de ganhar), a probabilidade de um jogador que troca de caixa ganhar é de 1/3 e a probabilidade de um jogador que troca de caixa perder é de 1/3. Portanto, as chances de trocar de caixa são as mesmas. Quando restam apenas duas caixas, a probabilidade de cada caixa conter o prêmio maior é de 50/50.
Hora de mais uma pergunta do "Deal or No Deal". Digamos que, depois de todas as ofertas do banqueiro e das participações especiais da Celine Dion, você fique com duas maletas: uma com US$ 500.000 e outra com US$ 1.000.000. A oferta do banqueiro será um pouco menor que US$ 750.000, eu imagino. Qual você escolheria? E se as duas maletas restantes fossem a de US$ 0,01 e a de US$ 1.000.000? Acho que tudo depende se você gosta de apostar ou não, e não tem nada a ver com probabilidades. O motivo da minha pergunta é que me pergunto se ALGUÉM algum dia ganhará US$ 1.000.000 (mesmo que tenha escolhido a maleta mágica).
Quando os prêmios se tornam quantias que mudam a vida, o jogador sábio deve jogar de forma conservadora, mesmo que isso signifique sacrificar a maximização do valor esperado. Uma boa estratégia seria maximizar a felicidade esperada. Uma boa função para medir a felicidade, na minha opinião, é o logaritmo da riqueza total. Vamos considerar uma pessoa com um patrimônio de US$ 100.000 que recebe duas ofertas: uma de US$ 0,01 e outra de US$ 1.000.000. Ao optar por "não aceitar", a felicidade esperada é de 0,5 * log(US$ 100.000,01) + 0,5 * log(US$ 1.100.000) = 5,520696. Seja b a oferta do banco, na qual o jogador é indiferente.
log(b) = 5,520696
b = 10 5,520696
b = $331.662,50.
Portanto, esse jogador hipotético deveria ser indiferente a uma oferta do banco de US$ 331.662,50. Quanto menor for sua riqueza antes do jogo, mais conservador você deve jogar. Normalmente, nas fases finais do jogo, as ofertas do banco se aproximam do valor esperado, às vezes um pouco acima. O único caso racional em que um jogador poderia ganhar o milhão é se ele tivesse muita riqueza antes do jogo e/ou as ofertas do banco fossem excepcionalmente baixas. Os produtores parecem gostar de pessoas trabalhadoras da classe média, então é improvável que vejamos alguém que possa se dar ao luxo de ser imprudente quando grandes quantias estão envolvidas. Eu também nunca vi o banco fazer ofertas abaixo de 90% do valor esperado nas fases finais do jogo. O momento em que veremos alguém ganhar o milhão será quando um jogador compulsivo entrar no programa e não conseguir parar. Quando isso acontecer, estarei torcendo pelo banqueiro.
Este texto é uma continuação do programa "Deal or No Deal", que assisti recentemente pela primeira vez. Sua análise parte do pressuposto de que a banca não sabe o valor do dinheiro na maleta. No entanto, no programa que assisti, na reta final, ambos os participantes escolheram uma maleta valiosa e ambos receberam (ou teriam recebido, já que um deles já havia desistido) ofertas acima do valor esperado (VE). No caso mais extremo, um jogador "teria recebido" uma oferta de US$ 687 mil quando as duas quantias restantes eram de US$ 500 mil e US$ 750 mil. A única explicação racional para isso é que o banqueiro sabe o valor da maleta do jogador e as ofertas feitas são baseadas nesse valor.
Essa é apenas a minha opinião, e não é necessário responder.
Obrigado por não esperar uma resposta, mas geralmente respondo a perguntas sobre programas de jogos. Em todos os episódios, eles afirmam que os valores nas maletas são colocados aleatoriamente e que nem Howie, nem o banqueiro, sabem os resultados. Isso nunca foi afirmado em "Let's Make a Deal", onde Monty Hall obviamente sabia. Eu também já vi o banqueiro oferecer um valor maior do que o esperado como última oferta, especialmente quando grandes quantias estão envolvidas. Na minha opinião, isso não acontece porque o banqueiro sabe o que está dentro da maleta do jogador. Na década de 1950, houve um grande escândalo quando se descobriu que o programa "21" , assim como outros, era manipulado. Não há nenhuma razão convincente para arruinar um programa de sucesso e a integridade de todos os programas de jogos para desviar parte do prêmio por meio das ofertas do banqueiro.
Posso apresentar três teorias sobre por que o banqueiro às vezes oferece mais do que a média dos demais casos.
- A série tenta retratar o banqueiro como alguém que se preocupa excessivamente com o dinheiro em seu escritório. Howie Mandel frequentemente comenta sobre o humor e o tom de voz do banqueiro. Talvez isso torne a série mais dramática, ao imaginarmos o banqueiro como um contador avesso ao risco, que prefere minimizar suas perdas a arriscar entregar um grande prêmio.
- O verdadeiro banqueiro é avesso a riscos. Isso foge um pouco da minha área de especialização, mas, pelo que entendi, programas de jogos e reality shows geralmente são produzidos por empresas independentes da emissora de televisão. Essas empresas menores procuram uma seguradora para mitigar o risco de os participantes ganharem os prêmios maiores. Nesse caso, a seguradora seria o verdadeiro banqueiro e pode estar influenciando o comportamento do banqueiro no programa. As seguradoras que asseguram coisas incomuns como essa não são gigantescas e podem preferir jogar pelo seguro quando grandes quantias estão envolvidas.
No seu exemplo, a oferta do banqueiro foi 9,92% superior ao valor esperado. Se o banqueiro estivesse seguindo o Critério de Kelly , tal oferta teria sido feita com um saldo total de apenas US$ 782.008, o que é inferior ao prêmio máximo. Nenhuma seguradora que se preze seria tão conservadora. Claramente, essa razão por si só não justifica a oferta no seu exemplo.
- O programa tenta fazer os participantes parecerem estúpidos e gananciosos. Programas como "Are You Smarter than a Fifth Grader?" e o quadro "Jaywalking" do The Tonight Show não fariam sucesso se não encontrássemos alguma satisfação em rir dos participantes com dificuldades em conhecimentos gerais. Os programas "Friend or Foe" e "The Weakest Link" foram excelentes em expor a ganância na natureza humana. Devo confessar que sinto uma certa satisfação quando um participante recusa uma oferta de valor acima do esperado e, no caso dele, fica com o valor menor.
Tendo a pensar que a razão é uma combinação dessas três razões, mas principalmente a terceira.
Se eu terminasse esta resposta aqui, certamente receberia comentários questionando se as ofertas hipotéticas do banqueiro realmente teriam sido feitas. A implicação seria que elas foram infladas para criar um efeito dramático. Registrei os detalhes de 13 jogos. Em um deles, com três maletas restantes (US$ 1.000, US$ 5.000 e US$ 50.000), a média foi de US$ 18.667 e a oferta foi de US$ 21.000. Isso representa 12,5% acima do valor esperado. Em outro jogo, com duas maletas restantes (US$ 400 e US$ 750.000), a média foi de US$ 375.200 e a oferta foi de US$ 400.000. Isso representa 6,6% acima do valor esperado. Portanto, não vejo motivos para questionar a integridade das ofertas hipotéticas.
Links:
Fórmula do Deal or No Deal : Esta página mostra fórmulas antigas e novas para calcular a oferta do banqueiro, com base no jogo gratuito do site Deal or No Deal.
Quanto você apostaria, no lugar de cada um, na rodada final do Jeopardy, com essas pontuações:
Jogador A: $10.000
Jogador B: $8.000
Jogador C: $ 3.500
Para começar, vou partir de algumas premissas. Primeiro, vou assumir que os três jogadores não têm conhecimento prévio sobre o comportamento de apostas no Final Jeopardy, exceto pelas probabilidades de acerto na tabela apresentada. Segundo, vou assumir que saber a categoria não ajuda em nada. Terceiro, também vou assumir que todos os três participantes querem ganhar, sem querer levar outro jogador junto em caso de empate.
Vamos começar com o jogador C. Ele deve prever que A pode apostar $6001 para se manter acima de B, caso B esteja certo. No entanto, se A estiver errado, isso reduziria suas apostas para $3999. C precisaria apostar pelo menos $500 e estar certo para vencer A nesse cenário. Contudo, na minha opinião, se você precisa estar certo para ganhar, é melhor apostar alto. Então, se eu fosse o CI, apostaria tudo.
B está dividido entre apostar alto ou baixo. Uma aposta baixa deve ser de US$ 999 ou menos, para se manter acima de C caso C esteja correto. A vantagem de uma aposta baixa é permanecer acima de C independentemente do resultado, na esperança de que A aposte alto e esteja errado. Uma aposta alta não precisa necessariamente ir até o final, mas pode ser que vá. A vantagem de uma aposta alta é esperar que A aposte baixo ou que aposte alto e esteja errado, mas ambos os casos exigem que B esteja certo.
Basicamente, A quer seguir o mesmo caminho que B. Uma aposta pequena para A pode variar de $0 a $1000, o que a manterá acima de B caso B aposte $999. Uma aposta grande deve ser de $6001, para garantir uma vitória se A estiver certo e ainda manter a esperança caso B faça uma aposta alta e todos os três jogadores estejam errados.
Para ajudar com as probabilidades dos oito resultados possíveis de respostas certas e erradas, consultei os resultados da Final Jeopardy das temporadas 20 a 24, do site j-archive.com (agora indisponível). Eis como os resultados se apresentam, com o jogador A na liderança, seguido pelo jogador B e, por último, o jogador C.
Possíveis Resultados no Desafio Final
| Jogador A | Jogador B | Jogador C | Probabilidade |
| Certo | Certo | Certo | 21,09% |
| Certo | Certo | Errado | 9,73% |
| Certo | Errado | Certo | 10,27% |
| Errado | Certo | Certo | 8,74% |
| Certo | Errado | Errado | 13,33% |
| Errado | Certo | Errado | 10,27% |
| Errado | Errado | Certo | 8,63% |
| Errado | Errado | Errado | 17,92% |
Usando o tipo de lógica da teoria dos jogos que explico no problema 192 do meu site mathproblems.info , descubro que A e B devem randomizar sua estratégia da seguinte forma.
O jogador A deve apostar alto com probabilidade de 73,6% e pouco com probabilidade de 26,4%.
O jogador B deve apostar alto com probabilidade de 67,3% e pouco com probabilidade de 32,7%.
O jogador C deve apostar alto com probabilidade de 100%.
Seguindo essa estratégia, a probabilidade de cada jogador vencer será a seguinte:
Jogador A: 66,48%
Jogador B: 27,27%
Jogador C: 6,25%
A título de curiosidade, com base na tabela acima, a probabilidade de o líder acertar a pergunta final é de 54,4%, para o segundo colocado, 49,8% e para o terceiro colocado, 48,7%. A probabilidade geral é de 51,0%.
Como observação prática, os jogadores têm conhecimento sobre o comportamento de apostas. Na minha opinião, eles tendem a apostar alto com mais frequência do que o matematicamente justifica. Curiosamente, acho que as apostas no Daily Double são conservadoras demais para o que seria matematicamente justificável. Acredito que um dos motivos pelos quais Ken Jennings se saiu tão bem foi a sua estratégia agressiva de apostas no Double Double. De qualquer forma, na realidade, se eu estivesse no programa, presumiria que os outros dois jogadores apostariam agressivamente. Portanto, minhas apostas seriam de US$ 6.000 como A (sendo gentil com B), US$ 0 como B e US$ 3.495 como C (deixando uma pequena margem de segurança, caso A, imprudentemente, aposte tudo ou tudo menos US$ 1 e esteja errado).
Antes que alguém me questione sobre como se pode sortear um número aleatório no local do evento, permitam-me sugerir a estratégia de Stanford Wong: usar o ponteiro dos segundos do relógio para sortear um número aleatório entre 1 e 60.
Um novo programa de jogos estreou no Reino Unido, chamado "The Colour of Money " (A Cor do Dinheiro). Um participante recebe aleatoriamente um valor-alvo, que pode variar de £55.000 a £79.000. Para ganhar dinheiro, ele escolhe 10 de 20 caixas eletrônicos, cada um contendo de £1.000 a £20.000, em incrementos de £1.000. Quando ele escolhe um caixa eletrônico, a contagem começa a partir de £1.000, em incrementos de £1.000.
O jogador pode gritar "Pare!" a qualquer momento e receberá o valor exibido na tela. Se o jogador não parar a tempo e a máquina ficar sem dinheiro, ele não receberá nada. Uma atendente fornece estatísticas, como o número de máquinas restantes para escolher, o valor restante para ganhar, o valor médio necessário por máquina para ganhar e os valores restantes nas máquinas.
Um jogador pode "jogar com as lacunas", aproveitando que, se uma sequência de máquinas premiadas, digamos, com £4.000, £5.000 e £6.000, uma máquina terá a garantia de atingir £7.000 assim que ultrapassar a marca de £3.000. Minha pergunta é: que tipo de estratégia um jogador deve usar?
Este é o tipo de coisa que eu poderia analisar por semanas. Infelizmente, li sua mensagem quase três meses depois de você tê-la escrito, devido a um grande acúmulo de perguntas para o "Pergunte ao Mágico". A página da Wikipédia parece indicar que o programa foi um fracasso e foi cancelado. No entanto, ainda é um problema interessante.
A atendente informa, de forma bem-humorada, a quantia média necessária por máquina restante para atingir o valor desejado. Depois de horas rabiscando, não consigo chegar a nada melhor do que definir uma meta de parada cerca de 25% acima da média necessária. Isso é apenas um palpite, então, por favor, não me peça para provar que é o ideal. Como você observou, aproveite os intervalos, nunca parando exatamente antes de atingir uma quantia já escolhida.
Quando restarem apenas duas máquinas, se o valor total necessário for de £13.000 ou menos, eu tentaria conseguir tudo na penúltima máquina. Se for de £14.000 ou mais, eu tentaria conseguir metade na próxima máquina.
Se eles decidirem trazer esse programa de volta, espero que meus leitores do Reino Unido me avisem. Esse é o tipo de enigma que poderia me deixar obcecado, como o enigma da Eternidade , que por coincidência (ou não) também era do Reino Unido.
PS: Por que vocês escrevem "colour" com "au" no Reino Unido? Não faz sentido para mim.
Qual é o prêmio médio por soco e a estratégia ideal para o jogo "Punch a Bunch" no programa "The Price is Right"?
Para quem não conhece as regras, elas estão explicadas no site do The Price Is Right . Por favor, dê uma olhada lá se você não conhece o jogo, pois vou presumir que você já conhece as regras. Há também vários vídeos do jogo no YouTube. Aqui está um vídeo antigo , que mostra uma segunda chance, mas o prêmio máximo na época era de apenas US$ 10.000. Agora é de US$ 25.000.
Primeiro, vamos calcular o valor esperado de um prêmio que não vem acompanhado de uma segunda chance. A tabela a seguir mostra que a média é de US$ 1.371,74.
Distribuição de prêmios Punch a Bunch sem segunda chance
| Prêmio | Número | Probabilidade | Vitória esperada |
| 25000 | 1 | 0,021739 | 543,478261 |
| 10000 | 1 | 0,021739 | 217,391304 |
| 5000 | 3 | 0,065217 | 326,086957 |
| 1000 | 5 | 0,108696 | 108,695652 |
| 500 | 9 | 0,195652 | 97,826087 |
| 250 | 9 | 0,195652 | 48.913043 |
| 100 | 9 | 0,195652 | 19,565217 |
| 50 | 9 | 0,195652 | 9,782609 |
| Total | 46 | 1.000000 | 1371,739130 |
Em segundo lugar, calcule o prêmio médio que oferece uma segunda chance. A tabela a seguir mostra que a média é de US$ 225.
Distribuição de Prêmios Punch a Bunch com Segunda Chance
| Prêmio | Número | Probabilidade | Vitória esperada |
| 500 | 1 | 0,250000 | 125.000000 |
| 250 | 1 | 0,250000 | 62.500000 |
| 100 | 1 | 0,250000 | 25.000000 |
| 50 | 1 | 0,250000 | 12.500000 |
| Total | 4 | 1.000000 | 225.000000 |
Em terceiro lugar, crie uma tabela de valores esperados com base no número de segundas chances que o jogador encontra. Isso pode ser calculado usando matemática simples. Por exemplo, a probabilidade de 2 segundas chances é (4/50) × (3/49) × (46/48). O ganho esperado, considerando s segundas chances, é de $1371,74 + s × $225. A tabela a seguir mostra a probabilidade e o ganho médio para 0 a 4 segundas chances.
Tabela de Retorno de Prêmios do Punch a Bunch
| Segundas chances | Probabilidade | Vitória média | Vitória esperada |
| 4 | 0,000004 | 2271,739130 | 0,009864 |
| 3 | 0,000200 | 2046,739130 | 0,408815 |
| 2 | 0,004694 | 1821,739130 | 8.551020 |
| 1 | 0,075102 | 1596,739130 | 119,918367 |
| 0 | 0,920000 | 1371,739130 | 1262.000000 |
| Total | 1.000000 | 1390,888067 |
Assim, o ganho médio por soco (incluindo o dinheiro adicional das segundas chances) é de US$ 1.390,89.
A tabela a seguir mostra minha estratégia de ganho mínimo a aceitar, de acordo com o número de tentativas restantes. Observe que o jogador pode chegar a US$ 1.400 com prêmios de US$ 1.000 + US$ 250 + US$ 100 + US$ 50 por meio de três segundas chances.
Estratégia de socos em grupo
| Socos restantes | Mínimo para ficar em pé |
| 3 | $ 5.000 |
| 2 | $ 5.000 |
| 1 | $ 1.400 |
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Qual seria a estratégia ideal para dividir seu dinheiro no programa de jogos Million Dollar Money Drop, se você não tivesse certeza da resposta?
Para benefício dos demais leitores, permitam-me revisar as regras primeiro.
- Uma equipe de jogadores começa com US$ 1.000.000.
- A equipe recebe uma questão de múltipla escolha.
- A equipe deve dividir o dinheiro dele entre as possíveis respostas. O valor apostado na resposta correta avançará para a próxima pergunta.
- A equipe deve descartar completamente pelo menos uma resposta possível, não apostando dinheiro nela.
- Esse processo se repete por várias rodadas. O jogador também tem uma chance de mudar de ideia.
Obviamente, se a equipe tem certeza da resposta, ele deve apostar tudo na resposta correta. Se a equipe conseguir reduzir a resposta a duas, mas atribuir a cada uma 50% de chance de estar correta, então eles devem dividir o dinheiro dele igualmente entre as duas opções.
A situação se complica quando a equipe tende a escolher uma resposta, mas não descarta completamente uma ou mais das outras. Vejamos um exemplo. Suponha que a equipe determine a probabilidade de cada resposta correta da seguinte forma: A 10%, B 20%, C 30%, D 40%. Como eles deveriam dividir o dinheiro dele?
Afirmo que a resposta é seguir o Critério de Kelly . Resumidamente, a equipe deve maximizar o logaritmo de sua riqueza a cada pergunta. Para isso, é preciso considerar quanta riqueza já se possui.
Digamos que sua riqueza atual, acumulada independentemente do programa, seja de US$ 100.000. Esta é a sua primeira pergunta, então você tem US$ 1.000.000 do dinheiro do programa para dividir. Primeiro, elimine a opção com a menor probabilidade, para cumprir as regras do programa. Em seguida, você quer maximizar 0,2 × log(100.000 + b * 1.000.000) + 0,3 × log(100.000 + c * 1.000.000) + 0,4 × log(100.000 + d * 1.000.000), onde a, b e c em minúsculas se referem à porcentagem atribuída a cada resposta.
Isso pode ser resolvido com cálculo e a resolução de uma equação trinomial, por tentativa e erro ou, minha preferência, usando a função "atingir meta" do Excel. Seja qual for o método escolhido, a resposta correta é atribuir 18,9% à alternativa B, 33,3% à C e 47,8% à D.
É claro que ninguém no programa conseguirá fazer todos esses cálculos no tempo disponível, sem mencionar que também é preciso movimentar uma grande quantidade de dinheiro nesse período. Meu conselho mais prático é simplesmente dividir o dinheiro proporcionalmente à sua avaliação da probabilidade de a resposta estar correta, assumindo que a opção menos provável não seja uma possibilidade. No exemplo, isso resultaria em uma divisão de 22,2% para a opção B, 33,3% para a C e 44,4% para a D.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
A Loteria de Michigan oferece um jogo para três jogadores com as seguintes regras: Existe alguma vantagem posicional em jogar por último nesta partida? Qual é a estratégia ideal para cada jogador? Aqui está um vídeodo YouTube mostrando a partida.
Primeiro, não há vantagem posicional em ser o último a jogar. Como os jogadores ficam em uma cabine à prova de som enquanto os jogadores anteriores tocam, a ordem não importa.
Em segundo lugar, deve haver um equilíbrio de Nash no jogo, onde uma estratégia para manter uma pontuação de pelo menos x pontos seja superior a qualquer outra estratégia. A questão é encontrar x.
O que eu fiz foi me perguntar qual seria a estratégia se, em vez de um cartão numerado de 1 a 100, cada jogador recebesse um número aleatório distribuído uniformemente entre 0 e 1, e procurar o ponto x onde um lógico perfeito seria indiferente entre permanecer no mesmo lugar e trocar de carta. Com essa resposta, é fácil aplicá-la a uma distribuição discreta de 1 a 100.
Vou parar de falar por aqui e deixar que meus leitores apreciem o problema. Veja os links abaixo para a resposta e a solução.
Resposta para uma distribuição contínua de 0 a 1 .
Resposta para uma distribuição discreta de 1 a 100.
Para ver minha solução, clique aqui (PDF) .
Essa questão foi levantada e discutida no meu fórum no Wizard of Vegas .
Supondo que não se saiba o preço de nada, qual é a estratégia ideal para o Jogo da Corrida no programa "O Preço Certo"?
Para quem não conhece as regras, o jogador recebe quatro etiquetas de preço e deve colocá-las em quatro itens. Ao terminar, ele puxa uma alavanca que indica o número de acertos. Se o jogador acertar menos de quatro, ele pode reorganizar as etiquetas e tentar novamente. O jogador pode tentar quantas vezes quiser em 45 segundos.
Meu conselho é sempre submeter uma seleção que tenha chance de vencer, considerando o histórico de seleções e pontuações anteriores. Se a primeira pontuação for 0, não inverta dois conjuntos de duas tags, mas mova tudo uma posição em qualquer direção.
Se você não conseguir calcular a lógica na hora, eu explico abaixo. Para usar essa estratégia, atribua as letras A, B, C e D às diferentes etiquetas. Em seguida, coloque-as na ordem mostrada, da esquerda para a direita no palco. Sempre comece com ABCD. Depois, consulte o histórico de pontuação abaixo e escolha a sequência de etiquetas indicada para aquela sequência de pontuação.
Se 0, então BCDA
Se 0-0, então CDAB
Se 0-0-0, então DABC (deve vencer)
Se 0-1, então BDAC
Se 0-1-0, então CADB (deve vencer)
Se 0-1-1, então CDBA
Se 0-1-1-0, então DCAB (deve vencer)
Se 0-2, então BADC
Se o placar estiver 0-2-0, então DCBA (deve vencer).
Se 1, então ACDB
Se 1-0, então BDCA
Se 1-0-0, então CABD
Se 1-0-0-1, então CBAC (deve vencer)
Se 1-1, então BDCA
Se 1-1-0, então CABD
Se 1-1-0-1, então CBAC (deve vencer)
Se 1-1-1, então BCAD (deve vencer)
Se 2, então ABDC
Se o placar estiver 2-0, então BACD (deve vencer).
Se 2-1, então ACBD
Se 2-1-0, então DBCA
Se 2-1-1, então ADCB
Se 2-1-1-0, então CBAD (deve vencer)
A tabela a seguir mostra a probabilidade de cada número total de giros. A célula inferior direita mostra um número esperado de giros de 10/3.
Jogo de Corrida
| Viradas | Combinações | Probabilidade | Retornar |
|---|---|---|---|
| 1 | 1 | 0,041667 | 0,041667 |
| 2 | 4 | 0,166667 | 0,333333 |
| 3 | 8 | 0,333333 | 1.000000 |
| 4 | 8 | 0,333333 | 1,333333 |
| 5 | 3 | 0,125000 | 0,625000 |
| Total | 24 | 1.000000 | 3,333333 |
Essa questão é discutida no meu fórum, Wizard of Vegas .
Qual é a probabilidade de um jogador qualquer ganhar US$ 25.000 no Showcase Showdown do programa The Price is Right?
Para esclarecer para os demais leitores, permita-me explicar do que você está falando. O Showcase Showdown é um jogo apresentado no programa de televisão The Price is Right. No Showcase Showdown, cada jogador gira uma roleta que tem a mesma probabilidade de parar em qualquer valor divisível por 0,05, de 0,05 a 1,00. Se o jogador não gostar do resultado da primeira rodada, pode girar novamente, somando o segundo resultado ao primeiro. No entanto, se o resultado for superior a 1,00, o jogador é imediatamente desclassificado. Em caso de empate, cada jogador tem direito a uma rodada de desempate, e quem obtiver o maior resultado vence. Se o empate persistir, o processo se repete até que o desempate seja resolvido.
O principal objetivo do Showcase Showdown é avançar para o Showcase. No entanto, também há prêmios em dinheiro imediatos, conforme descrito a seguir:
- Na primeira rodada, se algum jogador conseguir um total de $1,00, seja em uma única rodada ou na soma de duas rodadas, ele ganhará $1.000.
- Na primeira, e única, rodada de desempate, se a roleta parar em $0,05 ou $0,15, o jogador ganhará $10.000.
- Na primeira, e única, rodada de desempate, se a roleta parar em $1,00, o jogador ganhará $25.000.
Explico a estratégia ideal para o Showcase Showdown na coluna nº 101. Supondo que essa estratégia seja seguida, a tabela a seguir responde às suas perguntas e a várias outras.
Estatísticas do Showcase Showdown
| Pergunta | Responder |
|---|---|
| Previsões de ganhos de US$ 1.000 na primeira rodada. | 0,253790 |
| Probabilidade de empate entre 2 jogadores | 0,113854 |
| Probabilidade de empate entre 3 jogadores | 0,004787 |
| Espera-se que os vencedores da segunda rodada recebam US$ 10.000. | 0,024207 |
| Espera-se que os vencedores da segunda rodada recebam US$ 25.000. | 0,012104 |
| Valor total esperado do prêmio | $ 798,45 |
| Probabilidade de um determinado jogador ganhar $1000 | 0,084597 |
| Probabilidade de um determinado jogador ganhar $10000 | 0,008069 |
| Probabilidade de um determinado jogador ganhar $25000 | 0,004035 |
A última linha da tabela mostra que, se você chegar ao Showcase Showdown, sem considerar a ordem em que girou a roleta, suas chances de ganhar US$ 25.000 são de 0,004035, ou 1 em 248.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
No programa de sobrevivência Survivor, havia duas equipes, uma com nove jogadores e outra com seis. Elas foram então aleatoriamente divididas em três novas equipes de cinco pessoas cada. Cada nova equipe era composta por três membros da antiga equipe de nove jogadores e dois da antiga equipe de seis jogadores. Qual a probabilidade disso acontecer?
Vamos chamar o antigo time de nove jogadores de time 1 e o de seis jogadores de time 2. O número de maneiras de escolher três jogadores do time 1 e dois do time 2 é combin(9,3)×combin(6,2) = 1.260. O número total de maneiras de escolher cinco jogadores dentre 15 é combin(15,5) = 3.003. Portanto, a probabilidade de o primeiro time ser dividido em 3/2 a favor do time 1 é 1.260/3.003 = 41,96%.
Se isso acontecesse, o time 1 ficaria com seis jogadores restantes e o time 2 com quatro. O número de maneiras de escolher três jogadores do time 1 e dois do time 2 é combin(6,3)×combin(4,2) = 120. O número total de maneiras de escolher cinco dos 10 jogadores restantes é combin(10,5) = 252. Portanto, a probabilidade de o segundo time estar dividido 3/2 a favor do time 1, dado que o primeiro time já está dividido 3/2 dessa forma, é 120/252 = 47,62%.
Se as duas primeiras novas equipes forem divididas em 3/2, a favor da antiga equipe 1, então a equipe final será dividida em 3/2 entre os restantes.
Portanto, a resposta à sua pergunta é 41,96% × 47,62% × 100% = 19,98%.
Fórmulas:
combin(x,y)=x!/((y!*(xy)!)
x! = 1*2*3*...*x
Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .
Acho que James Holzhauer perdeu de propósito para Emma em seu último jogo. Minha prova é que ele vinha apostando alto em todos os jogos até então e, de repente, aposta baixo contra Emma. Suspeito que os produtores queiram que Ken Jennings apresente o programa depois que Alex sair. O programa seria mais dramático se o apresentador tivesse o histórico de vitórias e derrotas em ambos os programas e ganhasse dinheiro. Portanto, eles pagaram James para perder de propósito.
Deixe-me explicar o contexto. Em 3 de junho de 2019, James estava muito perto de quebrar o recorde de maior valor ganho em jogos regulares, que ainda permanece em US$ 2.520.700. A média de ganhos por jogo de James era muito maior do que o necessário para quebrar o recorde. Portanto, todos os olhares estavam voltados para ele em 3 de junho para ver o recorde ser quebrado.
Em vez disso, o que aconteceu foi que James não só não quebrou o recorde, como perdeu. A vencedora, Emma, jogou de forma muito estratégica, além de ter sido precisa com o botão e simplesmente responder corretamente. Ela jogou exatamente como James costumava jogar. Antes da rodada final do Jeopardy, a pontuação era a seguinte:
- Emma — US$ 26.600
- James — US$ 23.400
- Jay — US$ 11.000
Nessas situações, em que o segundo colocado tem mais da metade da pontuação do primeiro colocado, e o terceiro não, geralmente a decisão final cabe ao primeiro e ao segundo colocados: apostar alto ou baixo. Uma aposta alta para o primeiro colocado é suficiente para garantir a vitória, se estiver correta. Mais especificamente, duas vezes a pontuação do segundo colocado menos a pontuação do primeiro colocado mais um dólar. Foi exatamente isso que Emma fez com uma aposta de 2 × $23.400 - $26.600 + $1 = $20.201. Na maioria das vezes, o jogador em primeiro lugar faz isso.
No entanto, James não sabia o que Emma faria ao decidir sua aposta. A tabela a seguir mostra quem venceria de acordo com cada combinação de apostas.
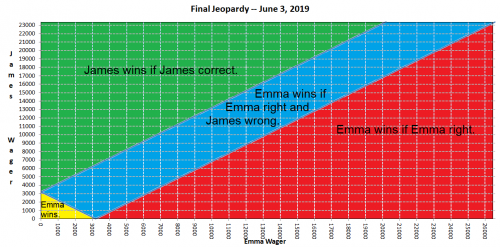
Clique na imagem para ver uma versão maior.
Se Emma apostar pelo menos US$ 20.201, ela garante a vitória caso acerte.
Se Emma apostar baixo, ela ganhará se (a) James apostar baixo ou (b) James apostar alto e estiver errado.
Se James apostar alto, ele ganha se (a) Emma apostar alto, Emma estiver errada e James estiver certo, ou (b) Emma apostar baixo e James estiver certo.
Se James apostar baixo, ele ganha se Emma apostar alto e errar.
Se fossem jogadores com lógica perfeita, ambos escolheriam aleatoriamente suas decisões. No entanto, raramente o líder opta pela resposta mais baixa nessas situações em que pode ser pego. Se James prevê que Emma escolherá a resposta mais alta, então ele definitivamente deve escolher a mais baixa. Dessa forma, ele não precisa acertar a resposta final para ganhar, basta torcer para que Emma erre.
A oferta real de James era o valor correto para cobrir Jay caso Jay apostasse tudo e estivesse certo: $23.400 - 2×$11.000 - $1 = $1.399, o que era considerado uma aposta baixa para vencer Emma.
Se estiver correto, James receberia um adicional de US$ 1.000 por ficar em segundo lugar, em comparação com o terceiro.
Em conclusão, rejeito completamente a teoria da conspiração de que James entregou o jogo. Ele jogou corretamente e perdeu devido a uma combinação de fatores, como enfrentar um adversário forte e o que a maioria das pessoas chamaria de "azar".
Links externos
- Hall da Fama do Jeopardy
- James Holzhauer no Jeopardy — Discussão no meu fórum no Wizard of Vegas.
Na rodada final do Jeopardy, qual é a estratégia ideal se o jogador em segundo lugar tiver mais de 2/3 do dinheiro do jogador em primeiro lugar? Considere que o jogador em terceiro lugar não é um fator relevante.
Antes de mais nada, gostaria de esclarecer um ponto. A análise a seguir baseia-se em médias estatísticas. Um jogador real deve fazer ajustes mentais considerando seu próprio conhecimento da categoria do Final Jeopardy, bem como estimar as chances de acerto do oponente.
Para responder à sua pergunta, primeiro examinei quatro temporadas de dados do Jeopardy Archive para ver as quatro combinações possíveis de acertos e erros do jogador em primeiro (líder) e segundo (perseguidor) na rodada final do Jeopardy.
Placar Final do Jeopardy
| Jogador principal | Jogador perseguindo correto | Jogador perseguindo incorreto | Total |
|---|---|---|---|
| Correto | 29,0% | 25,5% | 54,5% |
| Incorreto | 17,7% | 27,8% | 45,5% |
| Total | 46,8% | 53,2% | 100,0% |
Antes de prosseguirmos, vamos definir algumas variáveis:
x = Probabilidade de o jogador líder ter um resultado alto.
y = Probabilidade de o jogador perseguidor ser alto.
f(x,y) = Probabilidade do jogador com pontuação alta vencer.
Vamos expressar f(x,y) em termos de x e y da tabela acima:
f(x,y) = 0,823xy + 0,545x(1-y) + 0,468(1-x)y + (1-x)(1-y)
f(x,y) = 0,810xy - 0,455x - 0,532y + 1
Para encontrar os valores ótimos para x e y, vamos calcular a derivada de f(x,y) em relação a x e y.
f(x,y) d/dx = -0,455 + 0,810y = 0
Assim, y = 0,455/0,810 = 0,562
f(x,y) d/dy = -0,532 + 0,810x = 0
Assim, x = 0,523/0,810 = 0,657
Assim, o jogador com maior probabilidade de ganhar deve apostar alto com 65,7% de chance, e o jogador com menor probabilidade de ganhar deve apostar alto com 56,2% de chance.
Com base no que observei, acredito que o jogador com a melhor classificação aposta alto em mais de 65,7% das vezes; portanto, se eu estivesse em segundo lugar, apostaria baixo.
Se ambos os jogadores seguirem essa estratégia de aleatorização, a probabilidade de o jogador que estiver na frente vencer é de 70,1%.
Deixando a teoria de lado, se você estiver na liderança, preveja o que o jogador que está atrás fará e faça o mesmo. Se você estiver atrás, preveja a ação do jogador que está na liderança e faça o oposto. Essa estratégia vale para todos os torneios desse tipo.Essa questão é levantada e discutida no meu fórum, Wizard of Vegas .
No início de uma rodada do Jeopardy, por que alguns jogadores, como James Holtzhauer, começam escolhendo as perguntas de baixo para cima? Não faria mais sentido aquecer com as perguntas mais fáceis do início, em parte para garantir uma compreensão adequada da categoria, que às vezes é complicada?
O motivo é que as apostas "Daily Double" são colocadas nas três últimas linhas em 91,5% das vezes. A tabela a seguir mostra suas localizações no tabuleiro ao longo de 13.660 apostas "Daily Double" realizadas.
Localização do Daily Double
| Linha | Coluna 1 | Coluna 2 | Coluna 3 | Coluna 4 | Coluna 5 | Coluna 6 | |
|---|---|---|---|---|---|---|---|
| 1 | 5 | - | 3 | 3 | 2 | 3 | 16 |
| 2 | 280 | 137 | 216 | 167 | 207 | 140 | 1.147 |
| 3 | 820 | 442 | 677 | 658 | 643 | 472 | 3.712 |
| 4 | 1.095 | 659 | 982 | 907 | 895 | 627 | 5.165 |
| 5 | 787 | 403 | 670 | 671 | 613 | 476 | 3.620 |
| Total | 2.987 | 1.641 | 2.548 | 2.406 | 2.360 | 1.718 | 13.660 |
Fonte: J! Archive .
Aqui estão os mesmos dados, porém na forma de quantas vezes um "Daily Double" aparece em cada célula do tabuleiro.
Probabilidade de Dupla Diária
| Linha | Coluna 1 | Coluna 2 | Coluna 3 | Coluna 4 | Coluna 5 | Coluna 6 | |
|---|---|---|---|---|---|---|---|
| 1 | 0,0% | 0,0% | 0,0% | 0,0% | 0,0% | 0,0% | 0,1% |
| 2 | 2,0% | 1,0% | 1,6% | 1,2% | 1,5% | 1,0% | 8,4% |
| 3 | 6,0% | 3,2% | 5,0% | 4,8% | 4,7% | 3,5% | 27,2% |
| 4 | 8,0% | 4,8% | 7,2% | 6,6% | 6,6% | 4,6% | 37,8% |
| 5 | 5,8% | 3,0% | 4,9% | 4,9% | 4,5% | 3,5% | 26,5% |
| Total | 21,9% | 12,0% | 18,7% | 17,6% | 17,3% | 12,6% | 100,0% |
O motivo para procurar as rodadas Daily Double é que elas são uma ótima maneira de dobrar sua pontuação. A maioria dos participantes tem uma probabilidade de cerca de 80% a 90% de acertar qualquer dica. É um ótimo negócio receber o dobro do valor apostado em uma aposta com 80% a 90% de chance de ganhar. Um dos principais motivos pelos quais James Holtzhauer ganhou tanto foi a busca agressiva pelas rodadas Daily Double e a estratégia de apostar tudo na maioria das vezes que as encontrava. Foi também assim que ele perdeu para Emma, quando ela usou a mesma estratégia contra ele.
Qual a melhor estratégia para jogar o Jogo da Corrida no programa "O Preço Certo", considerando que o jogador não tem ideia dos valores dos prêmios?
Para benefício dos leitores que não estão familiarizados com o jogo, aqui está um vídeo dele.
Acredito que a seguinte estratégia resulta em um número médio mínimo de turnos. Existem muitas estratégias que a igualariam, mas não creio que alguma consiga superá-la.
Para usar a estratégia, rotule as quatro etiquetas de preço como 1, 2, 3 e 4. Coloque-as nos quatro prêmios de acordo com o histórico de quantas você acertou no passado, começando pela primeira rodada à esquerda.
Estratégia de Jogo de Corrida
| História | Prêmio 1 | Prêmio 2 | Prêmio 3 | Prêmio 4 |
|---|---|---|---|---|
| Nenhum | 1 | 2 | 3 | 4 |
| 0 | 2 | 1 | 4 | 3 |
| 0,0 | 3 | 4 | 2 | 1 |
| 0,0,0 | 4 | 3 | 1 | 2 |
| 0,0,2 | 3 | 4 | 1 | 2 |
| 0,0,2,0 | 4 | 3 | 2 | 1 |
| 0,2 | 2 | 3 | 4 | 1 |
| 0,2,0 | 4 | 1 | 2 | 3 |
| 0,2,1 | 2 | 4 | 1 | 3 |
| 0,2,1,0 | 3 | 1 | 4 | 2 |
| 1 | 1 | 3 | 4 | 2 |
| 1,0 | 2 | 4 | 3 | 1 |
| 1,0,0 | 3 | 1 | 2 | 4 |
| 1,0,0,0 | 4 | 2 | 1 | 3 |
| 1,1 | 1 | 4 | 2 | 3 |
| 1,1,0 | 2 | 3 | 1 | 4 |
| 1,1,0,0 | 3 | 2 | 4 | 1 |
| 1,1,0,0,0 | 4 | 1 | 3 | 2 |
| 2 | 2 | 1 | 3 | 4 |
| 2,0 | 1 | 2 | 4 | 3 |
| 2,1 | 1 | 3 | 2 | 4 |
| 2,1,0 | 4 | 2 | 3 | 1 |
| 2,1,1 | 1 | 4 | 3 | 2 |
| 2,1,1,0 | 3 | 2 | 1 | 4 |
A próxima tabela mostra a probabilidade de serem necessárias de 1 a 5 rodadas dentre as 24 maneiras possíveis de organizar as quatro etiquetas de preço.
Número de turnos necessários
| Viradas | Número | Probabilidade |
|---|---|---|
| 1 | 1 | 4,17% |
| 2 | 4 | 16,67% |
| 3 | 8 | 33,33% |
| 4 | 9 | 37,50% |
| 5 | 2 | 8,33% |
| Total | 24 | 100,00% |
Calculando o produto escalar, o número médio de turnos necessários, segundo essa estratégia, é de 3,29167.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Ouvi falar da regra dos dois terços nas apostas do Final Jeopardy. Você sabe algo sobre isso?
Sim. Refere-se a uma mudança de estratégia para o segundo colocado caso ele tenha mais de 2/3 da pontuação do primeiro colocado.
Vamos simplificar a situação para um jogo de dois jogadores, da seguinte forma:
- Situação A: O segundo lugar tem menos da metade da pontuação do primeiro lugar.
- Situação B: O segundo jogador tem entre 1/2 e 2/3 do primeiro lugar.
- Situação C: O segundo lugar tem mais de 2/3 dos votos do primeiro lugar.
Antes de prosseguir, gostaria de relembrar ao leitor uma mudança nas regras do Jeopardy referente a empates após a rodada final. Não é mais automático que ambos os jogadores avancem, mas sim que haja uma pergunta de desempate de morte súbita. Veja um exemplo dessa situação .
Situação A
Seja A = $10.000 e B = $4.000
O jogador A não deve arriscar perder apostando no máximo A-2B-1. Se não se sentir confiante na categoria, pode apostar $0. De qualquer forma, garante a vitória. Nesse caso, A deve apostar entre $0 e $1.999.
O jogador B não tem esperança, a menos que A aposte demais e erre. Nesse caso, B deve considerar a pontuação do terceiro colocado e tentar ficar à frente dele, se possível, ganhando US$ 2.000 pelo segundo lugar, em vez de US$ 1.000 pelo terceiro.
Situação B
Sejam A = $10.000 e B = $6.000
A estratégia para A é esperar que B aposte tudo e apostar o suficiente para cobrir 2B se estiver correto. No entanto, para maior segurança, ele não deve apostar muito a ponto de ficar abaixo de B se estiver errado. Nesse caso, ele deve apostar pelo menos 2B-A+1 e AB-1. Assim, o intervalo de apostas é de $2.001 a $3.999.
A estratégia de B é conseguir pelo menos o suficiente para passar A, caso esteja correto, e aumentar sua pontuação total. Nesse caso, US$ 4.001 e US$ 6.000.
Se ambos os jogadores agirem como esperado e seguirem essa estratégia, a única maneira do jogador B vencer é se A estiver errado e B estiver certo. A probabilidade disso acontecer é de aproximadamente 19%.
Situação C
Aqui as coisas ficam mais complicadas e envolvem mais teoria dos jogos e aleatorização.
Sejam A = $10.000 e B = $7.000.
Antes de prosseguirmos, é importante estimar a probabilidade de a pergunta da rodada final ser respondida corretamente. Com base nas temporadas 30 a 34, o jogador que ficou em primeiro lugar acertou 52% das vezes e o segundo lugar, 46%. No entanto, essas probabilidades são positivamente correlacionadas. Aqui está uma análise das quatro possibilidades:
- Ambas corretas: 27%
- Primeiro lugar correto, segundo lugar incorreto: 25%
- Primeiro lugar incorreto, segundo lugar correto: 19%
- Ambas incorretas, com 29% de erros.
Apesar de os dois primeiros jogadores terem uma média de 49% no Jeopardy, a probabilidade de ambos acertarem ou ambos errarem é de 56%.
É claro que esses valores podem variar dependendo da categoria, mas vamos simplificar e usar as probabilidades acima.
Nessa situação, o jogador B não precisa depender de A estar errado e B estar certo. Ele pode apostar pouco, digamos, $0, garantindo uma vitória se A estiver errado. Em outras palavras, se A apostar o suficiente para cobrir B, caso esteja certo, ele correria o risco de ficar abaixo de B se estivesse errado e B apostasse $0.
No entanto, se A previsse que B apostaria baixo, digamos, $0, então A poderia garantir a vitória apostando também $0. Basicamente, ambos os jogadores têm uma escolha a fazer: apostar baixo ou alto. A deve querer apostar da mesma forma que B, e B deve querer apostar de forma oposta à de B. Se ambos os jogadores fossem lógicos perfeitos, suas decisões seriam aleatórias.
Nesse caso, uma aposta alta de A deveria ser de 2B-A+1 a AB-1, a mesma que na situação B. Nesse caso, $2.999 e $4.001. Uma aposta baixa de A deveria ser de $0.
Uma aposta alta de B deve ser a mesma que na situação B, apostar o suficiente para ultrapassar A se estiver correto. Neste caso, $3.001 e $7.000. Uma aposta baixa de B deve ser de $0.
Peço desculpas se eu pular a parte dos cálculos e for direto às estratégias de aleatorização para ambos os jogadores.
O jogador A deve escolher uma pontuação alta com 62,3% de probabilidade e uma pontuação baixa com 37,7% de probabilidade.
O jogador B deve ter uma probabilidade alta de 61,2% e uma probabilidade baixa de 38,8%.
Considerando que ambos os jogadores sigam essa estratégia de aleatorização e que as probabilidades de acerto sejam as indicadas acima, a probabilidade de o jogador A vencer é de 65,2%.
Se o jogador A tivesse mais de 2/3 da pontuação do jogador B, sua probabilidade de vencer aumentaria para 81,0%.
Ambos os jogadores devem ter em mente a importância da regra 2/3 ao apostar no Double Jeopardy.