Nesta página
Por que o número de baralhos importa no blackjack
Introdução
Qualquer fonte respeitável sobre blackjack afirmará que existe uma correlação positiva entre o número de baralhos usados no blackjack e a vantagem da casa, considerando todos os outros fatores iguais. Em outras palavras, quanto menos baralhos, melhores as chances para o jogador recreativo. Esse fato é de conhecimento comum entre os jogadores de blackjack que têm pelo menos conhecimento suficiente para procurar um jogo com boas regras. No entanto, nunca vi uma análise aprofundada sobre o porquê disso. O objetivo deste artigo é esclarecer essa questão.
Antes de começarmos, permitam-me estabelecer algumas regras básicas. Estas foram escolhidas para serem o mais realistas possível, tendo em conta as condições do blackjack na altura em que este texto foi escrito, em 2020:
- O revendedor atinge o nível 17 com relativa suavidade.
- O Blackjack paga 3 para 2.
- O crupiê verifica se há blackjack com um dez ou um ás à mostra.
- O jogador pode dobrar a aposta em quaisquer duas cartas.
- O jogador não pode se render.
- O jogador pode dobrar a aposta após dividir o saque.
- O jogador pode dividir novamente qualquer par (incluindo ases) até três vezes.
- Utiliza-se um embaralhador contínuo (as cartas são embaralhadas após cada mão).
- O jogador utiliza estratégia básica.
Minha calculadora de vantagem da casa no blackjack indica que, sob essas regras, a vantagem da casa é a seguinte, de acordo com o número de baralhos:
Vantagem da casa no blackjack por baralho
| Baralhos | Borda da casa |
|---|---|
| 1 | 0,014% |
| 2 | 0,341% |
| 4 | 0,499% |
| 6 | 0,551% |
| 8 | 0,577% |
Esses números podem não coincidir exatamente com outras fontes confiáveis sobre blackjack. Acredito que quaisquer diferenças se devam ao uso de uma carta de corte ou à utilização, pelo jogador, de uma estratégia otimizada dependente da composição da mão. Em contrapartida, presumo que as cartas sejam embaralhadas após cada mão e que o jogador sempre siga a estratégia básica dependente do total.
Note que a diferença na vantagem da casa é de 0,563% entre oito baralhos e um baralho. Este artigo busca responder à questão de por que o número de baralhos tem um efeito tão significativo nas probabilidades.
Jogo equilibrado
Como ponto de partida, considero um jogo de blackjack simplificado, no qual as regras são exatamente as mesmas para o jogador e para o dealer, resultando em uma vantagem da casa de 0%, independentemente do número de baralhos. Em seguida, adiciono gradualmente as regras reais do blackjack, uma a uma, e examino como elas afetam a vantagem da casa em função do número de baralhos.
O jogo inicial hipotético de blackjack simplificado terá as mesmas regras descritas anteriormente, exceto:
- O jogador segue a estratégia de "imitar o crupiê".
- Ganhar no blackjack paga o mesmo valor apostado.
- Se tanto o jogador quanto o dealer ultrapassarem 21 pontos (ultrapassarem 21 pontos), o resultado é um empate (push).
Neste Jogo Equilibrado, a vantagem da casa é obviamente exatamente 0,000%, porque todas as regras afetam os dois lados igualmente.
Vantagem Posicional do Concessionário
Quem ganha no blackjack quando tanto o jogador quanto o dealer estouram? O dealer. Em outras palavras, o dealer tem uma vantagem posicional, pois quem estourar primeiro perde e o jogador precisa agir primeiro. Essa é a razão pela qual o dealer tem vantagem, apesar de muitas regras favorecerem o jogador. Ao adicionar essa regra ao Jogo de Equilíbrio e executá-la em simulações com um e oito baralhos, os retornos esperados para o jogador são os seguintes.
Valores esperados por mudança de regra
| Regra | Um baralho | Oito baralhos | Diferença |
|---|---|---|---|
| vantagem posicional do revendedor | -8,237% | -8,157% | -0,079% |
A tabela acima mostra que as probabilidades são piores para o jogador neste jogo hipotético com um baralho em comparação com oito baralhos. Isso ocorre porque, à medida que o número de baralhos diminui, a probabilidade de estourar aumenta. A seguir, apresenta-se a probabilidade de estourar neste jogo de "imitar o dealer", assumindo que o dealer joga sua mão mesmo que o jogador estoure primeiro.
- Um baralho = 27,333%
- Oito baralhos = 27,209%
O gráfico acima mostra que a probabilidade de qualquer um dos lados estourar é 0,124% maior em um jogo com um baralho em comparação com um jogo com oito baralhos. Existe alguma correlação entre os estouros de cada lado, então vamos analisar todas as quatro combinações de estouro do jogador e do dealer:
Probabilidades de quebra
| Jogador Fracassado | Prisão de traficantes | Um baralho | Oito baralhos | Diferença |
|---|---|---|---|---|
| Não | Não | 44,096% | 44,468% | -0,372% |
| Não | Sim | 19,095% | 19,051% | 0,044% |
| Sim | Não | 19,095% | 19,051% | 0,044% |
| Sim | Sim | 8,237% | 8,157% | 0,079% |
| Total | 90,524% | 90,728% | -0,204% |
O motivo pelo qual as probabilidades não somam 100% é que a tabela não contabiliza as mãos em que um dos lados tem um blackjack e a mão não é jogada de outra forma. A linha "Sim Sim" mostra as situações em que ambos os lados estouram, resultando em uma vitória para o dealer. Ela mostra que isso acontece 0,080% mais frequentemente em um jogo com um baralho em comparação com oito baralhos. Por quê? Se um dos lados estourou, deve ter sido depois de pedir carta com uma mão forte de 12 a 16 pontos. Essa mão deve ter consistido em pelo menos duas cartas. Enquanto isso, se um dos lados tivesse duas cartas de alto valor, ele pararia. Em outras palavras, pedir carta geralmente ocorre com mãos que têm cartas de valor menor que a média. Essa remoção de cartas baixas em situações de pedir carta faz com que as cartas restantes tenham um excedente de cartas altas. Esse efeito da remoção das cartas baixas antes de estourar é mais significativo em um jogo com um baralho.
Blackjack paga 3 para 2.
A próxima regra que adicionaremos ao Jogo Equilibrado será que um jogador que ganha no blackjack paga 3 para 2. A adição dessa regra à minha simulação resulta nos seguintes retornos esperados cumulativos para o jogador.
- Um baralho = -5,912%
- Oito baralhos = -5,894%
A tabela de resultados da simulação, incluindo uma linha para a adição desta regra, é a seguinte:
Valores esperados por mudança de regra
| Regra | Um baralho | Oito baralhos | Diferença |
|---|---|---|---|
| vantagem posicional do revendedor | -8,237% | -8,157% | -0,079% |
| No blackjack, o jogador vencedor paga 3 para 2. | -5,912% | -5,894% | -0,018% |
A diferença entre as duas linhas mostra o benefício para o jogador de um blackjack vencedor que paga 3 para 2:
- Um baralho = 2,325%
- Oito baralhos = 2,263%
- Diferença = 0,062%
Isso é fácil de verificar matematicamente, como segue. Seja d = número de baralhos. Usando a notação do Excel, a probabilidade de um blackjack vencedor é: probabilidade(blackjack do jogador) * (1-probabilidade(blackjack do dealer)) = (16*d)*(4*d)/combin(52*d,2) * [1-(16*d-1)*(4*d-1)/combin(52*d-2,2)
Probabilidade de ganhar no Blackjack
| Baralhos | Probabilidade |
|---|---|
| 1 | 4,649% |
| 2 | 4,578% |
| 4 | 4,544% |
| 6 | 4,532% |
| 8 | 4,527% |
Como visto acima, a probabilidade de ganhar no blackjack aumenta à medida que o número de baralhos diminui. Isso se deve simplesmente aos efeitos da remoção de cartas. Por exemplo, suponha que a primeira carta do jogador seja qualquer carta de valor 10. A probabilidade disso é 4/13, independentemente do número de baralhos. É fácil ver que, em um jogo com um único baralho, a probabilidade de obter um ás como segunda carta é 4/51 = 7,843%. Em um jogo com oito baralhos, essa probabilidade é 32/415 = 7,711%, que é 0,123% menor do que em um jogo com um único baralho. Em outras palavras, a razão pela qual a probabilidade de obter o ás é maior no jogo com um único baralho é que o baralho fica mais rico em ases depois que você remove um 10 dele. O mesmo acontece se a primeira carta for um ás; as cartas restantes terão mais cartas de valor 10 no jogo com um único baralho.
Além disso, se o jogador conseguir um blackjack, a probabilidade de o dealer conseguir um diminui à medida que o número de baralhos diminui. Isso ocorre porque, em um jogo com um único baralho, o jogador remove um ás e um 10 do baralho, o que torna muito mais difícil para o dealer conseguir um blackjack em comparação com um jogo com oito baralhos. Especificamente, a probabilidade de um blackjack do dealer, supondo que o jogador já tenha um, é de 3,673% com um baralho e 4,605% com oito baralhos. O jogador ganha meia unidade extra a cada blackjack. Para obter o valor de um blackjack vencedor pagando 3 para 2 em nosso hipotético jogo equilibrado, multiplique a probabilidade de um blackjack vencedor por 0,5 para obter essa meia unidade extra a cada vez. Isso resulta em uma vantagem para o jogador por número de baralhos, conforme segue:
Vantagem do jogador ao vencer no Blackjack
| Baralhos | Vantagem do Jogador |
|---|---|
| 1 | 2,325% |
| 2 | 2,289% |
| 4 | 2,272% |
| 6 | 2,266% |
| 8 | 2,263% |
Note que os benefícios matematicamente calculados de um blackjack vencedor pagar meia unidade extra correspondem aos resultados da simulação mostrados anteriormente para jogos com um e oito baralhos.
A tabela abaixo mostra uma lista atualizada das regras analisadas até o momento e seus benefícios para um jogador com um único baralho em comparação com um jogador com oito baralhos:
Efeito das Regras
| Regra | Benefício de um único deck |
|---|---|
| vantagem posicional do revendedor | -0,079% |
| No blackjack, o jogador vencedor paga 3 para 2. | 0,062% |
| Total | -0,018% |
Em seguida, vamos analisar a vantagem para o jogador de poder parar com um total fixo de 12 a 16. A estratégia básica dependente do total nesse intervalo é a mesma para qualquer número de baralhos, como segue:
- Com um total de 12, pare contra um dealer de 4 a 6, caso contrário, peça carta.
- Com um total de 13 a 16, pare contra um dealer de 2 a 6, caso contrário, peça carta.
A adição dessa estratégia à simulação resulta nos seguintes retornos esperados para o jogador:
- Um baralho = -2,209%
- Oito baralhos = -2,625%
A tabela de resultados da simulação abaixo inclui uma linha para a adição desta regra:
Valores esperados por mudança de regra
| Regra | Um baralho | Oito baralhos | Diferença |
|---|---|---|---|
| vantagem posicional do revendedor | -8,237% | -8,157% | -0,079% |
| No blackjack, o jogador vencedor paga 3 para 2. | -5,912% | -5,894% | -0,018% |
A diferença entre a segunda e a terceira fila mostra o efeito da liberdade do jogador de se posicionar em uma posição difícil entre 12 e 16.
- Um baralho = 3,703%
- Oito baralhos = 3,270%
- Diferença = 0,433%
A diferença entre esses dois valores mostra que o efeito dessa mudança de regra representa um ganho 0,433% maior para o jogador em um jogo com um único baralho em comparação com um jogo com oito baralhos. Contrariando a crença popular, isso explica a maior parte do motivo pelo qual um jogo com um único baralho oferece um ganho 0,563% maior para o jogador do que um jogo com oito baralhos.
Analisando mais detalhadamente o que acontece quando o jogador atinge totais difíceis de 12 a 16, enquanto o dealer não consegue, esta tabela mostra o benefício para o jogador decorrente de vários eventos que mudam devido ao fato de o jogador atingir menos totais difíceis, resultando em menos estouros para o jogador e mais estouros para o dealer, bem como mais confrontos perdidos para o dealer:
Possíveis resultados quando o jogador se posiciona em piso duro de 12 a 16
| Evento | Um baralho | Oito baralhos | Diferença |
|---|---|---|---|
| Menos prisões envolvendo apenas jogadores | 6,282% | 6,271% | 0,010% |
| Mais operações exclusivas para revendedores | 4,228% | 4,171% | 0,057% |
| Menos ambos quebram | 4,228% | 4,172% | 0,055% |
| Jogador vence menos confrontos diretos | -1,914% | -2,039% | 0,125% |
| O crupiê vence mais confrontos diretos. | -9,121% | -9,306% | 0,185% |
| Total | 3,703% | 3,270% | 0,433% |
A mesma tabela foi simplificada para mostrar a vantagem de ganhar mais devido ao dealer estourar com mais frequência e perder mais confrontos:
Resumo dos possíveis resultados quando o jogador se posiciona em piso duro de 12 a 16
| Evento | Um baralho | Oito baralhos | Diferença |
|---|---|---|---|
| Jogador quebrando menos benefício | 14,738% | 14,615% | 0,123% |
| Derrota no confronto direto | -11,035% | -11,345% | 0,310% |
| Total | 3,703% | 3,270% | 0,433% |
Em outras palavras, em um jogo com um único baralho, o jogador ultrapassará 14,738% menos frequentemente que o dealer ao seguir a estratégia básica com um total fixo de 12 a 16. No entanto, dessas mãos, em 75% das vezes o dealer não ultrapassará, resultando em sua vitória em um confronto direto com uma mão do jogador de 16 ou menos que não pode vencer. Em relação a todas as mãos, o jogador economiza 14,738% por ultrapassar menos, mas perde 11,035% em confrontos diretos, resultando em um ganho líquido de 3,703% em um jogo com um único baralho.
Essa vantagem é de apenas 3,270% em um jogo com oito baralhos. Levando tudo em consideração, o benefício de se posicionar estrategicamente entre 12 e 16 vale 0,433% a mais para o jogador em um jogo com um único baralho do que em um jogo com oito baralhos.
Por que a estratégia de parar é mais valiosa em um jogo com um baralho do que com oito? A resposta é semelhante à explicação de por que a vantagem posicional do dealer é mais significativa em um jogo com um único baralho. Há mais estouros em um jogo com um único baralho. Embora estourar mais vezes possa ser vantajoso para ambos os lados, é mais prejudicial para o jogador, pois ele perde quando ambos os lados estouram. Os totais de 12 a 16, quando o jogador para, provavelmente são compostos por mais cartas baixas do que altas. Isso deixa mais cartas altas no baralho, que podem potencialmente estourar o jogador. Os efeitos da remoção dessas cartas baixas, necessárias para melhorar a mão do jogador, são mais custosos em um jogo com um único baralho do que com oito. Em outras palavras, pedir cartas ruins é mais perigoso em um jogo com um único baralho. Portanto, parar é mais vantajoso em um jogo com um único baralho.
Segue abaixo uma tabela atualizada com a relação custo/benefício de cada alteração de regra:
Efeito das Regras
| Regra | Benefício de um único deck |
|---|---|
| vantagem posicional do revendedor | -0,079% |
| No blackjack, o jogador vencedor paga 3 para 2. | 0,061% |
| O jogador pode ficar em pé em terreno firme de 12 a 16 | 0,433% |
| Total | 0,415% |
Jogador pode dobrar
Em seguida, vamos analisar o benefício para o jogador de poder dobrar a aposta. Para estudar o efeito, configurei a simulação para seguir a estratégia de duplicação apropriada para o número de baralhos dado, que será apresentada mais adiante neste artigo. A adição dessa estratégia à simulação resulta nos seguintes retornos esperados para o jogador:
- Um baralho = -0,556%
- Oito baralhos = -1,245%
Esta tabela de resultados da simulação inclui uma linha para a adição desta regra:
Valores esperados por mudança de regra
| Regra | Um baralho | Oito baralhos | Diferença |
|---|---|---|---|
| vantagem posicional do revendedor | -8,237% | -8,157% | -0,079% |
| No blackjack, o jogador vencedor paga 3 para 2. | -5,912% | -5,894% | -0,018% |
| O jogador pode ficar em pé em terreno firme de 12 a 16 | -2,209% | -2,625% | 0,415% |
| O jogador pode dobrar | -0,556% | -1,245% | 0,689% |
A diferença entre a terceira e a quarta linha mostra o efeito do jogador ter livre arbítrio para dobrar, da seguinte forma:
- Um baralho = 1,653%
- Oito baralhos = 1,380%
- Diferença = 0,273%
A diferença entre esses dois valores mostra que o efeito dessa mudança de regra representa um ganho de 0,273% para o jogador em um jogo com um único baralho em comparação com um jogo com oito baralhos. Isso explica outra parte significativa do motivo pelo qual um jogo com um único baralho oferece um ganho de 0,563% em relação a um jogo com oito baralhos.
Por que dobrar é mais vantajoso em um jogo com um único baralho? Na maioria das vezes, quando o jogador dobra, será com um total fixo de 9 a 11 pontos. Dobrar é feito com duas cartas, então é preciso usar duas cartas de valor menor que a média para somar a um total baixo de 9 a 11. Se duas cartas de valor baixo forem removidas de um único baralho, a próxima carta terá 32% de chance de ser um dez, o que é obviamente bom ao dobrar com totais fixos. Enquanto isso, se duas cartas de valor baixo forem removidas de um sapato com oito baralhos, o efeito da remoção não é tão forte, diminuindo a probabilidade de a próxima carta ser um dez para 30,92%.
Segue abaixo uma tabela atualizada com a relação custo/benefício de cada alteração de regra. Observe que o benefício total de 0,689% supera a diferença final da vantagem da casa. Isso ocorre porque ainda não consideramos o efeito da divisão.
Efeito das Regras
| Regra | Benefício de um único deck |
|---|---|
| vantagem posicional do revendedor | -0,079% |
| No blackjack, o jogador vencedor paga 3 para 2. | 0,061% |
| O jogador pode ficar em pé em terreno firme de 12 a 16 | 0,433% |
| O jogador pode dobrar | 0,273% |
| Total | 0,689% |
Jogador pode dividir
Em seguida, analisei o benefício para o jogador de poder dividir as cartas. Para estudar o efeito, fiz com que a simulação seguisse a estratégia de divisão apropriada para o número de baralhos dado, que será apresentada mais adiante neste artigo. A adição dessa estratégia nos leva à estratégia básica completa. Não há outras diferenças de regras entre jogador e dealer para serem analisadas após a adição da divisão. Os retornos esperados do jogador na estratégia básica completa são:
- Um baralho = -0,012%
- Oito baralhos = -0,575%
A tabela de resultados da simulação, incluindo uma linha para a adição desta regra, é a seguinte:
Valores esperados por mudança de regra
| Regra | Um baralho | Oito baralhos | Diferença |
|---|---|---|---|
| vantagem posicional do revendedor | -8,237% | -8,157% | -0,079% |
| No blackjack, o jogador vencedor paga 3 para 2. | -5,912% | -5,894% | -0,018% |
| O jogador pode ficar em pé em terreno firme de 12 a 16 | -2,209% | -2,625% | 0,415% |
| O jogador pode dobrar | -0,556% | -1,245% | 0,689% |
| O jogador pode dividir | -0,012% | -0,575% | 0,563% |
A diferença entre a quarta e a quinta linha mostra o efeito do jogador ter livre arbítrio para dividir.
- Um baralho = 0,544%
- Oito baralhos = 0,669%
- Diferença = -0,125%
A diferença entre esses dois valores mostra que o efeito dessa mudança de regra é 0,125% menor para o jogador em um jogo com um único baralho em comparação com um jogo com oito baralhos.
A razão pela qual dividir é mais vantajoso em um jogo com oito baralhos, em comparação com um, é que as chances de obter um par nas duas primeiras cartas são maiores. Mais especificamente, com oito baralhos, usando a terminologia do Excel, a probabilidade é 13*combin(4*8,2)/combin(52*8,2) = 7,470%. Com um baralho, a probabilidade é 13*combin(4*1,2)/combin(52*1,2) = 5,882%.
Lembre-se também de que as regras básicas do jogo permitem a divisão das cartas até três vezes, ou até quatro mãos. Se duas cartas do mesmo valor forem removidas de um baralho, a probabilidade de obter esse mesmo valor na próxima carta é de 2/50 = 4,000%. Enquanto isso, para um jogo com oito baralhos, essa probabilidade é de 30/414 = 7,246%. Com menos divisões e redistribuções ocorrendo em um jogo com um único baralho, o valor da divisão, no geral, é menor. Isso explica por que o benefício da divisão diminui ao passar de oito para um baralho.
Ao adicionar o efeito negativo da divisão ao jogo com um único baralho, completamos nossa tabela sobre o efeito de várias regras no benefício de um jogo com um único baralho em comparação com oito baralhos.
Regra de um baralho: Benefício da vantagem posicional do dealer -0,079%; Blackjack vencedor paga 3 para 2 0,061%; Jogador pode parar em 12 a 16 (carta dura) 0,433%; Jogador pode dobrar 0,273%; Jogador pode dividir -0,125%; Total 0,563%.Note que a soma na célula inferior direita, de 0,563%, corresponde às diferenças fornecidas pela calculadora de vantagem da casa citada no início do artigo. Aqui está a mesma tabela listada em ordem de efeito:
Efeito das Regras
| Regra | Benefício de um único deck |
|---|---|
| vantagem posicional do revendedor | -0,079% |
| No blackjack, o jogador vencedor paga 3 para 2. | 0,061% |
| O jogador pode ficar em pé em terreno firme de 12 a 16 | 0,433% |
| O jogador pode dobrar | 0,273% |
| O jogador pode dividir | -0,125% |
| Total | 0,563% |
Tabelas de estratégia básica
A tabela a seguir mostra a estratégia básica apropriada para as regras e o baralho fornecidos.
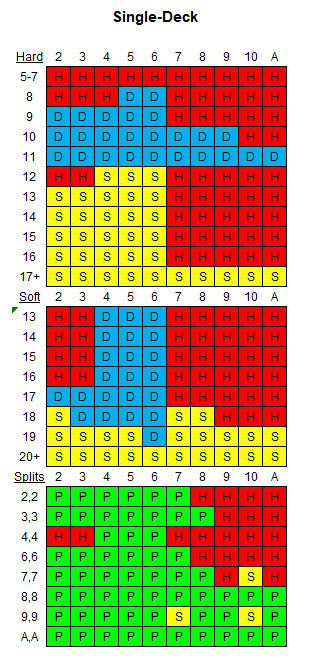
A tabela a seguir mostra a estratégia básica apropriada para as regras e oito baralhos fornecidos.
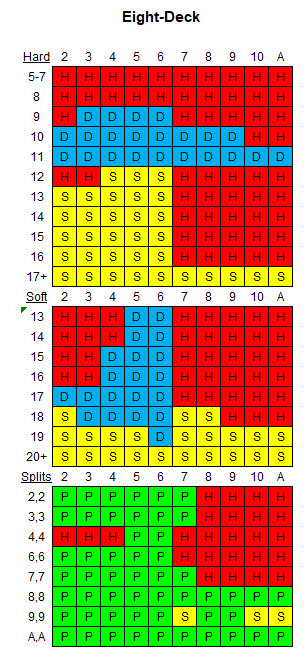
Tabelas de Valores Esperados
A tabela a seguir mostra o valor esperado de cada mão inicial no jogo com um baralho. A linha superior mostra a carta aberta do dealer. Os valores esperados são medidos antes de o dealer verificar se tem blackjack. A coluna "Total" mostra uma média ponderada dos valores esperados em cada linha, de acordo com a probabilidade de receber a mão. A célula inferior direita mostra o valor esperado do jogo como um todo.
Valores esperados em jogos de baralho único
Valores esperados por mão do jogador versus carta aberta do dealer com um baralho
| Jogador | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Ás | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0,1278 | -0,0968 | -0,0379 | 0,0227 | 0,0403 | -0,1191 | -0,1805 | -0,2624 | -0,3654 | -0,5443 | -0,2169 |
| 6 | -0,1477 | -0,1037 | -0,0519 | 0,0104 | 0,0371 | -0,1640 | -0,2343 | -0,3046 | -0,4015 | -0,5713 | -0,2469 |
| 7 | -0,1120 | -0,0701 | -0,0119 | 0,0528 | 0,0683 | -0,0690 | -0,2232 | -0,2948 | -0,3863 | -0,5765 | -0,2211 |
| 8 | -0,0174 | 0,0199 | 0,0826 | 0,1407 | 0,1498 | 0,0921 | -0,0565 | -0,2135 | -0,3136 | -0,5144 | -0,1286 |
| 9 | 0,1124 | 0,1923 | 0,2837 | 0,3753 | 0,3799 | 0,1951 | 0,1111 | -0,0519 | -0,2165 | -0,4146 | 0,0151 |
| 10 | 0,4262 | 0,4908 | 0,5494 | 0,6276 | 0,6241 | 0,4458 | 0,3145 | 0,1644 | -0,0528 | -0,2991 | 0,2316 |
| 11 | 0,5428 | 0,5922 | 0,6516 | 0,7176 | 0,7198 | 0,4785 | 0,3417 | 0,2240 | 0,0670 | -0,1848 | 0,3268 |
| 12 | -0,2518 | -0,2255 | -0,1915 | -0,1364 | -0,1194 | -0,2273 | -0,2925 | -0,3639 | -0,4175 | -0,5824 | -0,3131 |
| 13 | -0,2879 | -0,2411 | -0,1816 | -0,1344 | -0,1208 | -0,2861 | -0,3461 | -0,3764 | -0,4590 | -0,6106 | -0,3415 |
| 14 | -0,2900 | -0,2391 | -0,1835 | -0,1342 | -0,1209 | -0,3442 | -0,3612 | -0,4192 | -0,4957 | -0,6356 | -0,3644 |
| 15 | -0,2803 | -0,2379 | -0,1837 | -0,1388 | -0,1266 | -0,3590 | -0,4133 | -0,4703 | -0,5397 | -0,6677 | -0.3893 |
| 16 | -0,2863 | -0,2446 | -0,1872 | -0,1435 | -0,1450 | -0,3760 | -0,4254 | -0,4797 | -0,5482 | -0,6739 | -0,3978 |
| 17 | -0,1568 | -0,1216 | -0,0712 | -0,0445 | -0,0306 | -0,1217 | -0,3976 | -0,4154 | -0,4562 | -0,6560 | -0,2947 |
| 18 | 0,1072 | 0,1359 | 0,1538 | 0,1983 | 0,2031 | 0,3887 | 0,0956 | -0,1961 | -0,2242 | -0,4527 | -0,0185 |
| 19 | 0,3763 | 0,3774 | 0,3965 | 0,4449 | 0,4364 | 0,6101 | 0,5769 | 0,2642 | 0,0125 | -0,1586 | 0,2644 |
| A,2 | 0,0402 | 0,0711 | 0,1174 | 0,2130 | 0,2455 | 0,1074 | 0,0392 | -0,0141 | -0,1454 | -0,3991 | -0,0057 |
| A,3 | 0,0184 | 0,0447 | 0,1127 | 0,2042 | 0,2391 | 0,0605 | 0,0349 | -0,0602 | -0,1781 | -0,4205 | -0,0308 |
| A,4 | -0,0103 | 0,0237 | 0,0892 | 0,1753 | 0,2191 | 0,0339 | -0,0354 | -0,1136 | -0,2226 | -0,4533 | -0,0697 |
| A,5 | -0,0298 | -0,0019 | 0,0667 | 0,1490 | 0,2327 | -0,0239 | -0,0842 | -0,1666 | -0,2760 | -0,4900 | -0,1094 |
| A,6 | 0,0142 | 0,0743 | 0,1549 | 0,2805 | 0,2630 | 0,0597 | -0,0646 | -0,1348 | -0,2383 | -0,4810 | -0,0586 |
| A,7 | 0,1279 | 0,1867 | 0,3091 | 0,3482 | 0,3623 | 0,4118 | 0,1209 | -0,0873 | -0,1926 | -0,4433 | 0,0459 |
| A,8 | 0,3953 | 0,4157 | 0,4100 | 0,4593 | 0,4666 | 0,6146 | 0,6078 | 0,2882 | -0,0009 | -0,1938 | 0,2686 |
| A,9 | 0,6525 | 0,6415 | 0,6507 | 0,6810 | 0,6730 | 0,7732 | 0,7848 | 0,7656 | 0,4594 | 0,0943 | 0,5871 |
| A,10 | 1,5000 | 1,5000 | 1,5000 | 1,5000 | 1,5000 | 1,5000 | 1,5000 | 1,5000 | 1,4081 | 1,0409 | 1,4449 |
| A,A | 0,6384 | 0,6863 | 0,7417 | 0,8075 | 0,8289 | 0,6277 | 0,4865 | 0,3605 | 0,2080 | -0,1580 | 0,4744 |
| 2,2 | -0,0349 | 0,0396 | 0,1235 | 0,3014 | 0,3378 | 0,0137 | -0,1412 | -0,2224 | -0,3355 | -0,5246 | -0,1145 |
| 3,3 | -0,1082 | -0,0209 | 0,1607 | 0,3049 | 0,3395 | -0,0448 | -0,2232 | -0,3100 | -0,3986 | -0,5715 | -0,1646 |
| 4,4 | -0,0136 | 0,0268 | 0,1354 | 0,2680 | 0,2980 | 0,1104 | -0,0549 | -0,2063 | -0,3069 | -0,5065 | -0,0991 |
| 5,5 | 0,4441 | 0,5075 | 0,5870 | 0,6933 | 0,7084 | 0,4663 | 0,3227 | 0.1738 | -0,0510 | -0,2978 | 0,2444 |
| 6,6 | -0,0963 | 0,0132 | 0,1456 | 0,2786 | 0,1992 | -0,1933 | -0,3222 | -0,3862 | -0,4366 | -0,5989 | -0,2245 |
| 7,7 | -0,0546 | 0,0494 | 0,1879 | 0,2244 | 0,2396 | -0,0524 | -0,3804 | -0,4744 | -0,5556 | -0,6790 | -0,2508 |
| 8,8 | 0,1165 | 0,1873 | 0,2245 | 0,3287 | 0,3508 | 0,3040 | -0,0599 | -0,4017 | -0,4929 | -0,6389 | -0,1224 |
| 9,9 | 0,2052 | 0,2156 | 0,3070 | 0,4064 | 0,4080 | 0,4011 | 0,2067 | -0,0986 | -0,2041 | -0,4520 | 0,0666 |
| 10,10 | 0,6220 | 0,6323 | 0,6402 | 0,6718 | 0,6683 | 0,7647 | 0,7832 | 0,7440 | 0,4539 | 0,1383 | 0,5803 |
| Total | 0,1021 | 0,1388 | 0,1860 | 0,2391 | 0,2471 | 0,1473 | 0,0551 | -0,0435 | -0,1712 | -0,3891 | -0,0001 |
Valores esperados em um jogo de oito baralhos
Valores esperados por mão do jogador versus carta aberta do dealer com oito baralhos
| Jogador | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Ás | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0,1258 | -0,0929 | -0,0562 | -0,0175 | 0,018 | -0,1196 | -0,1871 | -0,266 | -0,3663 | -0,5291 | -0,2191 |
| 6 | -0,1389 | -0,1042 | -0,0677 | -0,0287 | 0,0085 | -0,1534 | -0,2192 | -0,2941 | -0,3902 | -0,5469 | -0,2395 |
| 7 | -0,1094 | -0,0760 | -0,0391 | -0,0004 | 0,0349 | -0,0689 | -0,2121 | -0,2866 | -0,3731 | -0,5526 | -0,2164 |
| 8 | -0,0234 | 0,0076 | 0,0427 | 0,0774 | 0,1079 | 0,0831 | -0,0595 | -0,2104 | -0,3079 | -0,4931 | -0,1316 |
| 9 | 0,0743 | 0,1277 | 0,1921 | 0,2580 | 0,3141 | 0,1745 | 0,0998 | -0,0522 | -0,2180 | -0,3962 | -0,0071 |
| 10 | 0,3653 | 0,4176 | 0,4704 | 0,5253 | 0,5723 | 0,3990 | 0,2895 | 0,1469 | -0,0535 | -0,2865 | 0,2056 |
| 11 | 0,4786 | 0,5264 | 0,5759 | 0,6271 | 0,6718 | 0,4653 | 0,3496 | 0,2271 | 0,0864 | -0,2297 | 0,3097 |
| 12 | -0,2535 | -0,2331 | -0,2041 | -0,1613 | -0,1208 | -0,2146 | -0,2741 | -0,3430 | -0,4273 | -0,5746 | -0,3146 |
| 13 | -0,2867 | -0,2461 | -0,2030 | -0,1611 | -0,1210 | -0,2713 | -0,3264 | -0,3858 | -0,4682 | -0,6049 | -0,3447 |
| 14 | -0,2870 | -0,2456 | -0,2034 | -0,1612 | -0,1211 | -0,3240 | -0,3707 | -0,4295 | -0,5059 | -0,6328 | -0,3694 |
| 15 | -0,2858 | -0,2456 | -0,2033 | -0,1616 | -0,1217 | -0,3683 | -0,4162 | -0,4715 | -0,5422 | -0,6597 | -0,3927 |
| 16 | -0,2866 | -0,2463 | -0,2038 | -0,1622 | -0,1236 | -0,4103 | -0,4547 | -0,5057 | -0,5721 | -0,6820 | -0,4128 |
| 17 | -0,1565 | -0,1205 | -0,0819 | -0,0461 | -0,0090 | -0,1085 | -0,3842 | -0,4223 | -0,4633 | -0,6636 | -0,2958 |
| 18 | 0,1098 | 0,1379 | 0,1648 | 0,1953 | 0,2211 | 0,3982 | 0,1045 | -0,1847 | -0,2394 | -0,4626 | -0,0208 |
| 19 | 0,3780 | 0,3949 | 0,4138 | 0.4372 | 0,4513 | 0,6153 | 0,5918 | 0,2848 | -0,0149 | -0,1753 | 0,2569 |
| A,2 | 0,0458 | 0,0737 | 0,1041 | 0,1376 | 0,2024 | 0,1207 | 0,0523 | -0,0350 | -0,1703 | -0,3789 | -0,0269 |
| A,3 | 0,0224 | 0,0507 | 0,0827 | 0,1366 | 0,2010 | 0,0769 | 0,0155 | -0,0733 | -0,2024 | -0,4031 | -0,0533 |
| A,4 | -0,0006 | 0,0294 | 0,0641 | 0,1328 | 0,1986 | 0,0368 | -0,0282 | -0,1123 | -0,2357 | -0,4281 | -0,0803 |
| A,5 | -0,0211 | 0,0088 | 0,0611 | 0,1301 | 0,2004 | -0,0070 | -0,0689 | -0,1507 | -0,2691 | -0,4532 | -0,1057 |
| A,6 | -0,0006 | 0,0558 | 0,1220 | 0,1933 | 0,2513 | 0,0545 | -0,0721 | -0,1479 | -0,2563 | -0,4626 | -0,0792 |
| A,7 | 0,1160 | 0,1749 | 0,2418 | 0,3000 | 0,3560 | 0,4014 | 0,1074 | -0,0990 | -0,2075 | -0,4205 | 0,0270 |
| A,8 | 0,3800 | 0,3993 | 0,4157 | 0,4389 | 0,4621 | 0,6159 | 0,5953 | 0,2878 | -0,0164 | -0,1795 | 0,2579 |
| A,9 | 0,6371 | 0,6455 | 0,6562 | 0,6699 | 0,6778 | 0,7732 | 0,7909 | 0,7591 | 0,4379 | 0,1070 | 0,5752 |
| A,10 | 1,5000 | 1,5000 | 1,5000 | 1,5000 | 1,5000 | 1,5000 | 1,5000 | 1,5000 | 1,3874 | 1,0388 | 1,4309 |
| A,A | 0,6072 | 0,6561 | 0,7062 | 0,7588 | 0,8058 | 0,6277 | 0,5001 | 0,3629 | 0,2059 | -0,1511 | 0,4411 |
| 2,2 | -0,0797 | -0,0089 | 0,0697 | 0,1700 | 0,2643 | 0,0087 | -0,1576 | -0,2385 | -0,3430 | -0,5115 | -0,1430 |
| 3,3 | -0,1305 | -0,0482 | 0,0500 | 0,1502 | 0,2425 | -0,0518 | -0,2189 | -0,2946 | -0,3899 | -0,5465 | -0,1859 |
| 4,4 | -0,0225 | 0,0080 | 0,0441 | 0,1066 | 0,2027 | 0,0857 | -0,0595 | -0,2096 | -0,3070 | -0,4921 | -0,1212 |
| 5,5 | 0,3676 | 0,4201 | 0,4748 | 0,5324 | 0,5814 | 0,4012 | 0,2910 | 0,1477 | -0,0534 | -0,2863 | 0,2074 |
| 6,6 | -0,1947 | -0,0972 | 0,0043 | 0,1075 | 0,1900 | -0,2189 | -0,2775 | -0,3453 | -0,4295 | -0,5767 | -0,2426 |
| 7,7 | -0,1233 | -0,0335 | 0,0669 | 0,1569 | 0,2508 | -0,0485 | -0,3765 | -0,4361 | -0,5129 | -0,6382 | -0,2497 |
| 8,8 | 0,0720 | 0,1452 | 0,2171 | 0,3005 | 0,3753 | 0,3195 | -0,0276 | -0,3893 | -0,5170 | -0,6660 | -0,1329 |
| 9,9 | 0.1943 | 0,2506 | 0,3196 | 0,3925 | 0,4551 | 0,3996 | 0,2308 | -0,0801 | -0,2369 | -0,4624 | 0,0585 |
| 10,10 | 0,6334 | 0,6442 | 0,6549 | 0,6688 | 0,6770 | 0,7723 | 0,7907 | 0,7566 | 0,4373 | 0,1124 | 0,5745 |
| Total | 0,0927 | 0,1262 | 0,1628 | 0,2025 | 0,2390 | 0,1453 | 0,0585 | -0,0403 | -0,1727 | -0,3712 | -0,0058 |
Diferenças no valor esperado (em %)
A tabela a seguir mostra o valor esperado no jogo com um baralho menos o valor esperado no jogo com oito baralhos, em termos percentuais.
Variação nos valores esperados de acordo com a mão do jogador versus a carta aberta do dealer (x100)
| Jogador | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Ás | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0,196 | -0,383 | 1,834 | 4.02 | 2,229 | 0,05 | 0,664 | 0,361 | 0,087 | -1,52 | 0,22 |
| 6 | -0,8770 | 0,0480 | 1,5840 | 3,9030 | 2,8630 | -1,0640 | -1,5170 | -1,0490 | -1,1320 | -2,4330 | -0,7380 |
| 7 | -0,2560 | 0,5920 | 2,7210 | 5,3240 | 3,3400 | -0,0070 | -1,1090 | -0,8160 | -1,3150 | -2,3840 | -0,4720 |
| 8 | 0,6060 | 1,2300 | 3,9870 | 6,3300 | 4,1900 | 0,9040 | 0,3020 | -0,3070 | -0,5740 | -2,1370 | 0,2910 |
| 9 | 3,8080 | 6,4600 | 9.1610 | 11,7320 | 6,5770 | 2,0670 | 1,1320 | 0,0300 | 0,1480 | -1,8380 | 2.2220 |
| 10 | 6,0970 | 7,3170 | 7,8980 | 10.2270 | 5.1830 | 4,6820 | 2,4980 | 1,7530 | 0,0720 | -1,2510 | 2,6040 |
| 11 | 6,4200 | 6,5830 | 7,5650 | 9,0560 | 4,8030 | 1,3220 | -0,7900 | -0,3170 | -1,9460 | 4,4940 | 1,7050 |
| 12 | 0,1670 | 0,7540 | 1,2640 | 2,4890 | 0,1350 | -1,2760 | -1,8390 | -2,0880 | 0,9840 | -0,7830 | 0,1460 |
| 13 | -0,1260 | 0,5070 | 2,1460 | 2,6670 | 0,0210 | -1,4780 | -1,9700 | 0,9410 | 0,9190 | -0,5660 | 0,3180 |
| 14 | -0,2970 | 0,6510 | 1,9930 | 2,6980 | 0,0150 | -2.0210 | 0,9460 | 1,0330 | 1,0240 | -0,2860 | 0,5000 |
| 15 | 0,5560 | 0,7690 | 1,9570 | 2,2820 | -0,4950 | 0,9270 | 0,2900 | 0,1190 | 0,2470 | -0,7990 | 0,3400 |
| 16 | 0,0300 | 0,1700 | 1,6680 | 1,8640 | -2,1330 | 3,4380 | 2,9220 | 2,6000 | 2,3870 | 0,8060 | 1,4950 |
| 17 | -0,0300 | -0,1100 | 1,0720 | 0,1630 | -2,1630 | -1,3190 | -1,3380 | 0,6910 | 0,7130 | 0,7580 | 0,1060 |
| 18 | -0,2560 | -0,2000 | -1,0990 | 0,2950 | -1,7950 | -0,9490 | -0,8890 | -1,1420 | 1,5210 | 0,9900 | 0,2340 |
| 19 | -0.1730 | -1,7470 | -1,7360 | 0,7660 | -1,4910 | -0,5200 | -1,4980 | -2,0590 | 2,7370 | 1,6770 | 0,7460 |
| A,2 | -0,5660 | -0,2590 | 1,3280 | 7,5340 | 4,3080 | -1,3290 | -1,3120 | 2.0900 | 2,4910 | -2.0210 | 2.1220 |
| A,3 | -0,4090 | -0,6000 | 3,0040 | 6,7580 | 3,8040 | -1,6410 | 1,9440 | 1,3040 | 2,4300 | -1,7440 | 2,2470 |
| A,4 | -0,9750 | -0,5720 | 2,5100 | 4,2580 | 2,0490 | -0,2980 | -0,7230 | -0,1290 | 1,3080 | -2,5210 | 1.0610 |
| A,5 | -0,8730 | -1,0720 | 0,5650 | 1,8950 | 3,2330 | -1,6930 | -1,5280 | -1,5890 | -0,6930 | -3,6740 | -0,3690 |
| A,6 | 1,4820 | 1,8480 | 3,2870 | 8,7240 | 1,1650 | 0,5180 | 0,7480 | 1,3090 | 1,7920 | -1,8340 | 2.0600 |
| A,7 | 1.1920 | 1,1830 | 6,7250 | 4,8180 | 0,6310 | 1,0410 | 1,3420 | 1,1640 | 1,4890 | -2,2860 | 1,8940 |
| A,8 | 1,5370 | 1,6390 | -0,5690 | 2,0370 | 0,4540 | -0,1320 | 1,2540 | 0,0390 | 1,5550 | -1,4310 | 1,0640 |
| A,9 | 1,5370 | -0,3990 | -0,5560 | 1,1160 | -0,4780 | 0,0020 | -0,6060 | 0,6480 | 2,1530 | -1,2700 | 1.1970 |
| A,10 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 2.0730 | 0,2070 | 1,3970 |
| A,A | 3,1200 | 3.0230 | 3,5450 | 4,8720 | 2,3070 | 0,0000 | -1,3620 | -0,2430 | 0,2140 | -0,6920 | 3,3340 |
| 2,2 | 4,4790 | 4,8510 | 5,3790 | 13.1380 | 7,3480 | 0,4980 | 1,6370 | 1,6100 | 0,7540 | -1,3140 | 2,8470 |
| 3,3 | 2,2320 | 2,7290 | 11.0750 | 15.4710 | 9.7010 | 0,7020 | -0,4300 | -1,5380 | -0,8700 | -2,4920 | 2,1250 |
| 4,4 | 0,8840 | 1,8800 | 9.1320 | 16.1400 | 9,5290 | 2,4760 | 0,4550 | 0,3380 | 0,0090 | -1,4460 | 2.2100 |
| 5,5 | 7,6550 | 8,7410 | 11.2230 | 16.0940 | 12,6990 | 6,5150 | 3,1720 | 2,6130 | 0,2380 | -1,1510 | 3,7020 |
| 6,6 | 9,8410 | 11.0360 | 14.1250 | 17.1060 | 0,9170 | 2,5610 | -4,4720 | -4,0910 | -0,7110 | -2,2180 | 1,8060 |
| 7,7 | 6,8730 | 8,2850 | 12.1030 | 6,7540 | -1,1240 | -0,3840 | -0,3830 | -3,8370 | -4,2660 | -4,0800 | -0,1170 |
| 8,8 | 4,4530 | 4.2080 | 0,7370 | 2,8160 | -2,4470 | -1,5490 | -3,2240 | -1,2460 | 2.4110 | 2,7050 | 1.0500 |
| 9,9 | 1.0910 | -3,5070 | -1,2560 | 1,3820 | -4,7120 | 0,1480 | -2,4060 | -1,8530 | 3,2860 | 1,0450 | 0,8060 |
| 10,10 | -1,1490 | -1,1970 | -1,4750 | 0,2960 | -0,8740 | -0,7630 | -0,7510 | -1,2620 | 1,6580 | 2,5910 | 0,5780 |
| Total | 0,9370 | 1,2510 | 2.3110 | 3,6590 | 0,8050 | 0,1970 | -0,3390 | -0,3210 | 0,1480 | -1,7900 | 0,5620 |
Leitura complementar
O livro "A Teoria do Blackjack", de Peter Griffin, oferece a melhor abordagem sobre o tema deste artigo que já vi. Ele trata do assunto no capítulo 8, intitulado "Muitos Baralhos e Regras Diferentes", que utiliza um conjunto de regras básicas diferente e calcula a diferença entre um baralho e infinitos baralhos. Ele nem sempre fornece números exatos para tudo, mas parafraseia a distribuição da diferença de 0,69% sob suas premissas da seguinte forma:
- Dobrando a aposta: Quase metade de 0,69%
- Blackjacks dos jogadores: 0,07%
- Dividir: Mais do que compensa a vantagem do blackjack.
- Na posição 12 a 16: “Presumivelmente a discrepância restante.”
Griffin prossegue listando os benefícios de várias mudanças nas regras, tanto para decks com um único baralho quanto para decks infinitos.
Agradecimentos
Gostaria de agradecer a Don Schlesinger por seus sábios conselhos na análise e revisão deste artigo.


