Probabilidade - Quebra-cabeças
Tenho interesse em obter informações específicas sobre as probabilidades de rolar dados. Se você tiver 6 dados e os rolar todos de uma vez, a probabilidade de obter todos o número 1 é de 1 em 46.656. Minha pergunta é: qual a probabilidade de obter de um a cinco números 1? Gostaria muito de saber qual a fórmula que deve ser usada para calcular esse tipo de problema.
A probabilidade de rolar x uns em y dados é combin(y,x)*(1/6) x *(5/6) yx . Veja minha seção sobre probabilidades no pôquer para uma explicação da função combin(x,y). Por exemplo, a probabilidade de rolar 4 uns é combin(6,4)*(1/6) 4 *(5/6) 2 = 0,803755%.
Número de uns em seis dados
| Uns | Probabilidade |
|---|---|
| 0 | 0,3348980 |
| 1 | 0,4018776 |
| 2 | 0,2009388 |
| 3 | 0,0535837 |
| 4 | 0,0080376 |
| 5 | 0,0006430 |
| 6 | 0,0000214 |
| Total | 1.0000000 |
Oito jogadores de golfe foram a um novo campo. O responsável pelos caddies colocou 8 sacos de golfe em quatro carrinhos aleatoriamente. Os jogadores colocaram 8 bolas de golfe marcadas em um chapéu. As bolas foram lançadas para o ar. As duas bolas mais próximas uma da outra formavam pares. Em todos os casos, os sacos de golfe dos pares já estavam no mesmo carrinho. Qual é a probabilidade de os sacos de golfe terem sido emparelhados corretamente antes do lançamento?
A resposta por fórmula para o número de combinações seria combin(8,2)*combin(6,2)*combin(4,2)/fact(4) = 25*15*6/24 = 105. Outra maneira de resolver o número de combinações seria escolher um jogador de golfe aleatoriamente. Há 7 pessoas possíveis para formar dupla com ele. Em seguida, escolha outro jogador de golfe aleatoriamente dentre os seis restantes. Há 5 pessoas possíveis para formar dupla com ele. Depois, escolha outro jogador de golfe aleatoriamente dentre os quatro restantes. Há 3 pessoas possíveis para formar dupla com ele. Portanto, o número de combinações é 7*5*3 = 105. Assim, a resposta é 1 em 105.
Um amigo me enviou isso , e eu fiquei me perguntando se existe alguma fórmula que explique como isso funciona.
Muitas vezes, esses enigmas numéricos de leitura da mente funcionam devido a uma peculiaridade matemática interessante. Se a soma dos dígitos de um número é divisível por 9, então o próprio número é divisível por 9. Vamos tentar com o número de telefone do Las Vegas Tropicana (702-739-2222). A soma dos dígitos é 7+0+2+7+3+9+2+2+2+2 = 36. 36 é divisível por 9, então 702739222 também deve ser divisível por 9. Aqui está uma prova disso.
- Seja n um número inteiro qualquer. Expresse n como d 0 *1 + d 1 *10 + d 2 *100+ d 3 *1000+ ... + d n *10 n , onde d n é o primeiro dígito, d n-1 é o segundo, e assim por diante.
- n = [d 0 + d 1 + d 2 + ... + d n ] + [d 1 *9 + d 2 *99+ d 3 *999+ ...+ d n *999...9 ( um número com n noves)]
- n = [d 0 + d 1 + d 2 + ... + d n ] + 9*[d 1 *1 + d 2 *11+ d 3 *111+ ... d n *111...1 (um número com n uns)]
- Qualquer número inteiro é divisível por 9. Portanto, se d₀ + d₂ + d₃ + ... + dₙ , ou a soma dos dígitos, for divisível por 9, então o número inteiro também será divisível por 9.
Agora que já fizemos essa demonstração, podemos analisar este truque de mágica. O problema pede que você escolha um número qualquer. Em seguida, reorganize os dígitos para formar um segundo número. Depois, subtraia o número menor do número maior.
A resposta sempre terá uma soma de dígitos divisível por 9. Por quê? Para cada dígito no número original, ele aparece em algum outro lugar no outro número. Analisando um conjunto de dígitos por vez, substituindo todos os outros números por zero, podemos reduzir cada conjunto a +/- n*[10 x - 10 y ] (onde x>=y e n é o dígito) = +/-n *10 y * (10 xy - 1) = 10 y * (um número composto apenas de noves) = um número divisível por 9.
Vejamos um exemplo. Suponha que o número original seja 1965. Embaralhe-o para obter 6951. 6951 - 1965 = 6*(1000-10) + 9*(100-100) + 5*(10-1) + 1*(1-1000) = 6*990 + 9*0 + 5*9 + 6*-999. Observe que cada parte é divisível por 9; portanto, o número obtido após a subtração também deve ser divisível por 9 e, finalmente, a soma dos dígitos também é divisível por 9.
O truque pede que você circule um número diferente de 0 e insira a soma de todos os outros dígitos. O programa então só precisa adicionar um número ao número que você inseriu para que a soma seja divisível por 9. Por exemplo, se você disse que a soma dos seus dígitos era 13, então você deve ter circulado um 5, porque 13 + 5 = um número divisível por 9.
O motivo pelo qual você não pode circular um zero é que, se você fizesse isso e depois digitasse um número que já é divisível por 9, o programa não saberia dizer se você circulou um 0 ou um 9.
Ótimo site. Costumo consultá-lo como um apostador com interesse em probabilidade e estatística, mas esta pergunta, na verdade, se relaciona ao meu trabalho. Meu departamento de RH insiste que eu classifique minha pequena equipe (5 pessoas) seguindo uma curva normal: um entre os 5% melhores funcionários, um entre os 20% seguintes, um entre os 50% seguintes, um entre os 20% seguintes e um entre os 5% piores. A empresa tem aproximadamente 5.000 funcionários. Qual é a probabilidade de uma amostra tão pequena se encaixar nessa distribuição?
Obrigado pelo elogio. Este é um bom problema. A probabilidade de que exatamente um funcionário esteja nos 5% piores é 5*(0,05)*(0,95) ⁴ = 0,203627. Dado que um funcionário está nos 5% piores, a probabilidade de que exatamente um esteja nos próximos 20% é 4*(0,2/0,95)*(0,75/0,95) ³ = 0,414361. Considerando esses dois funcionários com baixo desempenho, a probabilidade de que exatamente um esteja nos próximos 50% dos 75% restantes é 3*(0,5/0,75)*(0,25/0,75) ² = 0,222222. A probabilidade de que um dos dois restantes esteja nos 20% piores dos 25% é 2*(0,2/0,25)*(0,05/0,25) = 0,32. Multiplicando todas essas probabilidades, obtemos 0,006, ou 3/5 de 1%.
Para o colega que fez a pergunta sobre estatísticas de ordem ( coluna nº 100 ), tenho duas ressalvas: uma pequena e uma grande. Seu método não fez uma correção para população finita, o que reconheço ser trivial com 5.000 funcionários, mas certamente não seria se houvesse 20 funcionários!
Mais importante ainda, você assume implicitamente que os gerentes não têm influência sobre seus funcionários. Suponha que bons gerentes, por meio de contratações e demissões criteriosas, ou por meio de habilidades motivacionais acima da média, elevem o nível médio de seus funcionários. Sem levar em conta esse efeito, teremos um viés para cima ou para baixo nas probabilidades resultantes. Tenho certeza de que você sabia disso, mas estou atento a essa questão porque realizo muitos cálculos como esse em casos de discriminação, e a falha em ajustar para fatores que podemos ajustar (neste caso, um efeito específico do grupo) pode frequentemente levar as pessoas a conclusões errôneas.
Agradeço pelos pontos importantes. No entanto, a alternativa à falta de controle sobre a distribuição das avaliações de desempenho é a inflação dessas avaliações. O gerente se verá na posição de atribuir notas infladas para manter sua equipe satisfeita. Como funcionário público há dez anos, falo com alguma experiência sobre isso. Quando lecionava na UNLV, não havia um padrão de média de notas da turma, mas havia certas expectativas sobre como deveria ser a curva de notas no final do semestre. Pelo menos em um ambiente universitário, eu achava que isso constituía uma política razoável. Talvez em um ambiente corporativo, um meio-termo baseado no bom senso também seja o mais adequado.
Existem problemas famosos não resolvidos que desafiam os matemáticos da área de jogos de azar? Algo como o Último Teorema de Fermat no mundo das apostas. Se sim, poderia compartilhar um exemplo?
Boa pergunta. Não consigo pensar em nenhum.
Como funciona: www.1800gotjunk.com/genie/ ?
Vamos expressar seu número como 10t + u. Você deve subtrair cada dígito, resultando em 10t + utu = 9t, um número divisível por 9. Observe como todos os números divisíveis por 9 têm o mesmo elemento, que é aquele previsto pelo gênio.
Estou prestes a fazer um exame de certificação profissional. O regulamento prevê que:
- O exame será composto por 7 disciplinas.
- Para cada disciplina, serão feitas 60 questões de múltipla escolha.
- Cada questão de múltipla escolha terá quatro alternativas, mas apenas uma correta.
- Para ser aprovado, o candidato deve obter uma média geral de pelo menos 75% e não pode ter uma nota inferior a 65% em nenhuma disciplina.
Minha pergunta é: se um candidato simplesmente chutar todas as respostas, qual a chance de ele passar no exame? Ou seja, qual a probabilidade de passar no exame por pura sorte?
Para atingir a nota mínima de 75%, o aluno precisa acertar pelo menos 315 das 420 questões. O número esperado de acertos por palpite é de 420 * 0,25 = 105. O desvio padrão é (420 * 0,25 * 0,75)^0,5 = 8,87412. Portanto, o candidato precisa superar a expectativa em 210 questões, ou 210 / 8,87412 = 23,66432 desvios padrão. A probabilidade de isso acontecer é extremamente baixa. Se todos os seres vivos da Terra fizessem esse teste, respondendo aleatoriamente, duvido que alguém ou alguma coisa passaria. Nem vou mencionar o outro requisito.
Se o time de futebol americano de uma universidade tem 10% de chance de vencer o primeiro jogo, 30% de chance de vencer o segundo e 65% de chance de perder ambos os jogos, qual é a probabilidade de ele vencer exatamente uma vez?
Se assumíssemos que os jogos são independentes, a probabilidade de perder ambos seria de 90% * 70% = 63%. Mas, como você disse que a probabilidade de perder ambos é, na verdade, de 65% (que é maior que 63%), isso significa que os dois eventos estão correlacionados. Se a probabilidade de perder ambos é de 65% e a probabilidade de perder apenas o jogo 2 é de 70%, então a probabilidade de ganhar o jogo 1 e perder o jogo 2 deve ser de 5%. Usando a mesma lógica, a probabilidade de perder o jogo 1 e ganhar o jogo 2 deve ser de 25%. Isso deixa apenas 5% de probabilidade de ganhar ambos os jogos. Portanto, a probabilidade de ganhar exatamente uma vez é de 25% + 5% = 30%.
No programa de jogos Let's Make a Deal, há três portas. Digamos, por exemplo, que duas portas revelam uma cabra e uma revela um carro novo. O apresentador, Monty Hall, escolhe dois participantes para escolherem uma porta. Toda vez que Monty abre primeiro uma porta que revela uma cabra, digamos que desta vez a porta era do primeiro participante. Embora Monty nunca tenha feito isso, e se ele oferecesse ao outro participante a chance de trocar de porta, para a outra porta que ainda não foi aberta? Ele deveria trocar?
Sim! A chave para este problema é que o apresentador está predestinado a abrir uma porta com um bode. Ele sabe qual porta tem o carro, então, independentemente das portas escolhidas pelos jogadores, ele sempre pode revelar um bode primeiro. A questão é conhecida como o "Paradoxo de Monty Hall". Grande parte da confusão em torno dela se deve ao fato de que, frequentemente, quando a questão é formulada, não fica claro que o apresentador sabe onde está o carro e sempre revela um bode primeiro. Acho que parte da culpa recai sobre Marilyn Vos Savant , que formulou a questão de forma inadequada em sua coluna. Vamos supor que o prêmio esteja atrás da porta 1. A seguir, vejamos o que aconteceria se o jogador (o segundo participante) tivesse a estratégia de não trocar de porta.
- Jogador escolhe a porta 1 --> jogador ganha
- Jogador escolhe a porta 2 --> jogador perde
- Jogador escolhe a porta 3 --> jogador perde
A seguir, veja o que aconteceria se o jogador adotasse uma estratégia de troca de personagens.
- O jogador escolhe a porta 1 --> O anfitrião revela a cabra atrás da porta 2 ou 3 --> O jogador troca para a outra porta --> O jogador perde
- O jogador escolhe a porta 2 --> o apresentador revela a cabra atrás da porta 3 --> o jogador troca para a porta 1 --> o jogador vence
- O jogador escolhe a porta 3 --> O apresentador revela a cabra atrás da porta 2 --> O jogador troca para a porta 1 --> O jogador vence
Portanto, ao não trocar de arma, o jogador tem 1/3 de chance de ganhar. Ao trocar de arma, o jogador tem 2/3 de chance de ganhar. Logo, o jogador definitivamente deveria trocar de arma.
Para saber mais sobre o paradoxo de Monty Hall, recomendo o artigo na Wikipédia .
Discordo da sua resposta à pergunta sobre Monty Hall na coluna de 19 de novembro de 2004. Supondo que o carro esteja atrás da porta um, existem, na verdade, quatro possibilidades, como segue, onde o prêmio está atrás da porta 1.
- O jogador escolhe a porta 1 --> mostra a porta 2 --> muda para a porta 3 e perde.
- O jogador escolhe a porta 1 --> mostra a porta 3 --> muda para a porta 2 e perde.
- O jogador escolhe a porta 2 --> mostra a porta 3 --> muda para a porta 1 e ganha.
- O jogador escolhe a porta 3 --> mostra a porta 2 --> muda para a porta 1 e ganha.
Como você pode ver, a probabilidade de ganhar é de 50%, independentemente de você trocar ou não. Além disso, é totalmente contra o senso comum pensar que trocar seria melhor.
Seu erro foi assumir que cada um desses eventos tem 25% de probabilidade. A seguir, apresentamos a probabilidade correta de cada evento.
- O jogador escolhe a porta 1 (1/3) * mostrada 2 (1/2) = o jogador perde (1/6)
- O jogador escolhe a porta 1 (1/3) * mostrada 3 (1/2) = o jogador perde (1/6)
- O jogador escolhe a porta 2 (1/3) * mostrada 3 (1/1) = o jogador ganha (1/3)
- O jogador escolhe a porta 3 (1/3) * mostrada 2 (1/1) = o jogador ganha (1/3)
Assim, os eventos perdedores têm uma probabilidade total de 2*(1/6) = 1/3 e os eventos vencedores têm uma probabilidade total de 2*(1/3) = 2/3.
Com cinco opções de recheio, quantas pizzas diferentes você pode fazer, com qualquer número de recheios?
Há 1 opção sem recheio, 5 opções com 1 recheio, 10 opções com 2 recheios, 10 opções com 3 recheios, 5 opções com 4 recheios e 1 opção com 5 recheios. Portanto, a resposta é 1 + 5 + 10 + 10 + 5 + 1 = 32. Outra maneira de resolver é verificar se o recheio pode ser usado ou não. Assim, o total é 2 × 5 = 32.
Vi no jornal na semana passada que o último terremoto que devastou a Indonésia ocorreu em 26 de dezembro. Também mostrou que, dos oito terremotos mais mortais dos últimos 100 anos, três aconteceram em 26 de dezembro. Fiquei pensando qual a probabilidade de três terremotos de grande magnitude ocorrerem no mesmo dia, sabendo disso: terremotos dessa magnitude (8,0 ou superior) acontecem apenas uma vez por ano. O último grande terremoto foi exatamente um ano antes, em 26/12/2003, no Irã (probabilidade de dois terremotos consecutivos?). Aguardo sua resposta.
Após descobrir que a alegação de que os furacões na Flórida atingiram apenas condados onde Bush votou era uma farsa (veja a coluna de 17 de outubro de 2004 ), passarei a ser mais cético em relação a essas supostas coincidências. De acordo com o Centro Nacional de Informações sobre Terremotos , dos 11 maiores terremotos desde 1990, apenas o mais recente, de 2004, ocorreu em 26 de dezembro. O terremoto iraniano que você mencionou teve apenas magnitude 6,7, o que está longe de figurar entre os oito maiores.
Com quantos ovos você começa se, a cada dia, você vende metade dos ovos mais meio ovo; após 3 dias, você não tem mais nenhum ovo? No final de cada dia, o número de ovos é um número inteiro.
Vamos considerar d (de dia) como o número de ovos no início do dia e n (de noite) como o número no final. O problema nos diz que d/2 - ? = n. Então, vamos resolver d em função de n.
d/2 = n + ?
d = 2n + 1
Assim, no terceiro dia, n=0, logo d=1.
No segundo dia, n=1, então d=3.
No terceiro dia, n=3, então d=7.
Então, pronto, você começou com 7 ovos.
Imagine uma ilha habitada por 10 pessoas, onde a política funciona da seguinte forma: a cada dia, um ilhéu é escolhido aleatoriamente para ser chefe por exatamente um dia; após esse dia, outro ilhéu é escolhido aleatoriamente (portanto, o mesmo ilhéu que acabou de ser chefe tem 1/10 de chance de ser chefe novamente). A questão a ser resolvida é: em média, quantos dias teriam que se passar para que cada ilhéu tivesse sido chefe pelo menos uma vez?
Bastará um dia para que uma pessoa tenha servido como chefe. No segundo dia, a probabilidade de um novo chefe ser nomeado é de 0,9. O número esperado de dias necessários para se obter um novo chefe, se a probabilidade diária for de 0,9, é 1/0,9 = 1,11. Isso é válido para qualquer probabilidade: o número esperado de tentativas até um sucesso é 1/p. Portanto, após duas pessoas terem servido, a probabilidade de um novo chefe ser nomeado no dia seguinte é de 0,8. Assim, o período de espera para um terceiro chefe é de 1/0,8 = 1,25 dias. A resposta é a soma dos períodos de espera, que é 1/1 + 1/0,9 + 1/0,8 + ... + 1/0,1 = 29,28968 dias.
O raio do círculo é 1. O triângulo é equilátero. Calcule a área de cada região colorida.
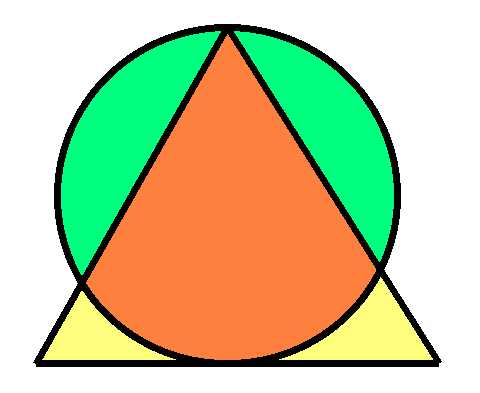
Não quero revelar a resposta para quem quiser resolver o problema por conta própria. Para a resposta e a solução, visite meu outro site mathproblems.info , problema 189.
Imagine que você ganhou um concurso em que, no intervalo de um jogo da NBA, você tem o direito de cobrar um lance livre e, se acertar, ganha US$ 1 milhão. Além disso, você pode continuar cobrando lances livres, com o dobro da pontuação ou sem nenhuma, até errar ou decidir parar. Se você tem uma taxa de acerto de 75% nos lances livres, quando você pararia? Será que algum dia você pararia? Em algum momento, o dinheiro começa a significar cada vez menos. O que você faria?
Em algum momento, você deve recusar uma boa aposta porque os riscos são muito altos. Pessoalmente, acho que uma boa medida do prazer que se obtém com o dinheiro é o logaritmo do valor. A base do logaritmo não importa, então vamos usar 10. No entanto, não podemos usar um logaritmo menor que 10, então digamos que o prazer seja 0 para qualquer valor menor que dez. Então, no seu exemplo, vamos supor que você tenha $0 antes de ganhar o $1.000.000 na sua primeira tentativa. Agora você tem log(1.000.000) = 6 unidades de felicidade. O valor esperado da sua felicidade ao fazer outra tentativa gratuita é 0,75 * log(2.000.000) + 0,25 * 0 = 4,975772. Isso é menor que 6, então, neste caso, você deveria pegar o milhão e ir embora. No entanto, poderia ser diferente se você já tivesse algum dinheiro. Digamos que você já tenha $200.000. Então, sua felicidade ao desistir é log(1.200.000) = 6,07918. Sua felicidade ao arriscar o milhão e tentar novamente é 0,75*log(2.200.000) + 0,25*log(200.000) = 6,082075, então você arriscaria a segunda tentativa. Se você ganhasse, sua escolha seria entre log(2.200.000) = 6,34242 e 0,75*log(4.200.000) + 0,25*log(200.000) = 6,29269. Nesse caso, você não deveria tentar uma terceira vez e, em vez disso, desistir com o prêmio de US$ 2.000.000. O ponto de equilíbrio para aceitar a primeira dobrada é um patrimônio existente de US$ 191.487. Para aceitar duas dobradas, você precisaria ter US$ 382.975 em outros recursos.
Lembro-me de que, se 22 pessoas estiverem em uma sala, a probabilidade de duas delas comemorarem o mesmo aniversário [mês e dia, não ano] é igual. Esqueci como fazer o cálculo para provar isso. Você poderia, por favor, me explicar?
Acho que já respondi isso antes, mas o ponto de equilíbrio (50/50) está mais próximo de 23. Para simplificar, vamos ignorar os anos bissextos. A resposta completa seria ordenar as 23 pessoas de alguma forma. A probabilidade de a pessoa nº 2 ter um aniversário diferente do da pessoa nº 1 é 364/365. A probabilidade de a pessoa nº 3 ter um aniversário diferente dos aniversários das pessoas nº 1 e nº 2, assumindo que sejam diferentes entre si, é 363/365. Continue repetindo até a pessoa 23. A probabilidade é, portanto, (364/365)*(363/365)*...*(343/365) = 49,2703%. Assim, a probabilidade de não haver nenhuma correspondência é de 49,27% e a de haver pelo menos uma correspondência é de 50,73%. Outra solução é o número de permutações de 23 aniversários diferentes dividido pelo número total de maneiras de escolher 23 números aleatórios de 1 a 365, que é permut (365,23)/365 23 = 42.200.819.302.092.400.000.000.000.000.000.000.000.000.000.000.000.000.000.000 / 85.651.679.353.150.300.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 = 49,27%.
Os salários semanais dos professores em um estado seguem uma distribuição normal com média de $490 e desvio padrão de $45. Qual é a probabilidade de um professor escolhido aleatoriamente ganhar mais de $525 por semana? Não me lembro como calcular a probabilidade apenas com base na média e no desvio padrão, sem considerar a população.
Isso seria US$ 35 acima da média, ou 7/9 de desvios padrão. A probabilidade de estar mais de 7/9 de desvios padrão acima das expectativas seria 1-Z(7/9) = 1- 0,78165 = 0,21835.
Duas pessoas estão jogando pedra, papel e tesoura. Presume-se que o jogo não envolva estratégia. Se estiverem jogando "melhor de 3" e o jogador A vencer a primeira rodada, qual a probabilidade de o jogador B vencer a partida?
O jogador B precisaria ganhar as próximas duas (sem contar empates), então a probabilidade é (1/2)*(1/2) = 1/4.
Olá, resolvi te perguntar isso porque não consigo encontrar a resposta em lugar nenhum na internet. Espero que você possa responder: Quais são as chances de existirmos? Seja na Terra ou em qualquer outro lugar do universo? Não é uma pergunta de jogo, mas uma pergunta que todos deveríamos saber para podermos apreciar as probabilidades que superamos simplesmente por estarmos vivos!
Acredito que a probabilidade de existir vida inteligente em qualquer lugar da galáxia seja muito alta. A Equação de Drake busca estimar o número de ocorrências de vida inteligente na galáxia, que, dependendo dos números inseridos, chega a uma cifra de cerca de um milhão. No entanto, também não há evidências concretas de que essas civilizações já nos visitaram ou fizeram contato. Assim, a famosa Questão de Fermi é: "Onde está todo mundo?". Acredito que a falta de evidências de outras formas de vida inteligente lança dúvidas sobre a Equação de Drake, mas ainda assim estimaria o número de civilizações inteligentes em nossa galáxia em torno de 1000. Isso considerando apenas a nossa galáxia; existem bilhões de galáxias por aí. Contudo, a distância entre as galáxias é tão vasta que não faz muito sentido discutir viagens ou comunicação entre elas. Portanto, para responder à sua pergunta, eu diria aproximadamente 99,9%.
Suponha que um hotel tenha 10.000.000 de quartos e 10.000.000 de chaves eletrônicas. Devido a um erro de computador, cada chave é programada com um código aleatório, com uma probabilidade de 1 em 10.000.000 de estar correto. O hotel está lotado. Qual é a probabilidade de que pelo menos um cliente tenha uma chave funcional?
A resposta exata é 1-(9.999.999/10.000.000) 10.000.000 = 0,632121. Isso também é o mesmo que (e-1)/e com sete casas decimais.
Há uma prova com 75 questões de múltipla escolha. Cada questão contém 4 alternativas, sendo apenas 1 correta. A nota mínima para aprovação é 50%. Qual a probabilidade de ser aprovado na prova chutando todas as respostas?
1 em 635.241.
Em apostas ao vivo, se um tenista tem uma chance "p" de ganhar um game, qual a chance que ele tem de ganhar um set?
Pelo que entendi das regras do tênis, o vencedor de um set é o primeiro a ganhar seis games, com uma vantagem de pelo menos dois games, exceto em caso de empate em 6-6, que resulta em um único tie-break. A tabela a seguir mostra a probabilidade de vencer um set, dada a probabilidade de vencer um game.
Probabilidades no tênis
| Probabilidade Vitória no jogo | Probabilidade Definir Vitória |
| 0,05 | 0,000003 |
| 0,1 | 0,000189 |
| 0,15 | 0,001899 |
| 0,2 | 0,009117 |
| 0,25 | 0,028853 |
| 0,3 | 0,06958 |
| 0,35 | 0,138203 |
| 0,4 | 0,23687 |
| 0,45 | 0,361085 |
| 0,5 | 0,5 |
| 0,55 | 0,638915 |
| 0,6 | 0,76313 |
| 0,65 | 0,861797 |
| 0,7 | 0,93042 |
| 0,75 | 0,971147 |
| 0,8 | 0,990883 |
| 0,85 | 0,998101 |
| 0,9 | 0,999811 |
| 0,95 | 0,999997 |
A fórmula para qualquer probabilidade de ganhar um jogo p e perder q é 1* p⁶ + 6* p⁶ *q + 21* p⁶ * q² + 56* p⁶ * q³ + 126* p⁶ * q⁴ + 252* p⁷ * q⁵ + 504* p⁷ * q⁶
Você está em um barco com uma pedra, em um lago de água doce. Você joga a pedra no lago. Em relação à margem, o nível da água sobe, desce ou permanece o mesmo? Meus colegas acham que o nível da água permanecerá o mesmo.
O nível da água em relação à margem diminuirá. Dentro do barco, a pedra pressiona a canoa para baixo, empurrando a água ao seu redor para cima. A quantidade de água deslocada é igual em peso à da pedra. Por exemplo, uma pedra de 4,5 kg deslocará 4,5 kg de água para cima. Quando a pedra for jogada ao mar, o peso não importará, mas sim o seu volume. Assim, a pedra empurrará para cima uma quantidade de água igual ao seu volume. A massa de uma pedra é maior que a da água, portanto, a pedra desloca mais água pressionando-a para baixo do que dentro dela. Consequentemente, o nível do lago será mais alto com a pedra na canoa do que no fundo do lago.
Como é que isso funciona?
- Pegue uma calculadora. (Você não conseguirá fazer isso de cabeça.)
- Digite os três primeiros dígitos do seu número de telefone (NÃO O CÓDIGO DE ÁREA).
- Multiplique por 80
- Adicionar 1
- Multiplique por 250
- Adicione os últimos 4 dígitos do seu número de telefone.
- Adicione novamente os últimos 4 dígitos do seu número de telefone.
- Subtraia 250
- Divida o número por 2.
Você reconhece a resposta?
Vamos chamar os três primeiros dígitos do seu número de telefone de x e os quatro últimos de y. Agora vamos ver o que eu tenho em cada etapa.
- Preparar!
- X
- 80x
- 80x+1
- 250*(80x+1) = 20000x+250
- 20000x+250+y
- 20000x+250+2y
- 20000x + 250 + 2y - 250 = 20000x + 2y
- (20000x+2y)/2 = 10000x+y
Então, é claro que isso vai ser igual ao seu número de telefone. Precisamos do multiplicador 10000x para mover o prefixo quatro casas para a esquerda e, em seguida, adicionamos os últimos quatro dígitos.
Está acontecendo um sorteio de um carro de US$ 27.000, com bilhetes à venda a seis por US$ 500,00 ou um por US$ 100,00. Sessenta e oito bilhetes já foram vendidos e amanhã é o prazo final para compra. Sei que, para ter 50% de probabilidade de ganhar, preciso gastar US$ 5.666,44, e para ter 66,66% de probabilidade de ganhar, preciso gastar US$ 11.332,88 (certo?). Quanto devo gastar (ou quantos bilhetes devo comprar) para praticamente garantir que "ganhe" o carro? (90%? 95%?) Vale a pena participar desse sorteio, ou preciso gastar o valor do carro?
Você está certo em relação às probabilidades de 1/2 e 2/3. Se você comprar t bilhetes, sua probabilidade de ganhar é t/(68+t). Portanto, para uma probabilidade de 90%, resolva para t da seguinte forma.
0,9 = t/(68+t)
0,9*(68+t) = t
61,2 = 0,1t
t = 612, ou $51.000
Para 95%...
0,95 = t/(68+t)
0,95(68+t) = t
64,6 = 0,05t
t = 1292, ou $107.666,67
Supondo que o carro valha US$ 27.000 para você, você deve parar de comprar bilhetes assim que o próximo bilhete vendido não aumentar sua probabilidade de ganhar o suficiente para justificar o preço.
Para que um bilhete valha o preço, ele deve aumentar sua probabilidade de ganhar em p, onde...
27000*p=(500/6)
p=0,003086
Digamos que t seja o número de ingressos que você comprou, sendo que comprar mais um ingresso é indiferente para você.
[(t+1)/(t+68+1)] − [t/(t+68)] = 0,003086
[(t+1)/(t+69)] − [t/(t+68)] = 0,003086
[((t+1)*(t+68))/((t+69)*(t+68))] − [(t*(t+69))/((t+68)*(t+69))] = 0,003086
[((t 2 +69t+68)/((t+69)*(t+68))] − [(t 2 +69t)/((t+68)*(t+69))] = 0,003086
68/((t+68)*(t+69)) = 0,003086
((t+68)*(t+69)) = 220,32
t² + 137t + 4692 = 22032
t² + 137t - 17340 = 0
t=(-137+/-(137 2 -4*1*-17340) 2 )/2
t = 79,9326
Vamos testar isso inserindo alguns valores para ingressos comprados, assumindo que o jogador sempre pode comprar ingressos a $500/6 = $83,33 cada.
Com 79 bilhetes, seu custo é 79*(500/6) = $6.583,33, sua probabilidade de ganhar é 79/(79+68) = 53,74%, seu retorno esperado é $27.000*0,5374 = $14.510,20 e seu lucro esperado é $14.510,20 - $6.583,33 = $7.926,87.
Com 80 bilhetes, seu custo é de 80*(500/6) = $6.666,67, sua probabilidade de ganhar é de 80/(80+68) = 54,04%, seu retorno esperado é de $27.000*0,5405 = $14.594,59 e seu lucro esperado é de $14.594,59 - $6.666,67 = $7.927,92
Com 81 bilhetes, seu custo é 81*(500/6) = $6.750,00, sua probabilidade de ganhar é 81/(81+68) = 54,36%, seu retorno esperado é $27.000*0,5436 = $14.677,85 e seu lucro esperado é $14.594,59 - $6.750,00 = $7.927,85.
Assim, podemos ver que o ganho máximo esperado atinge o pico em 80 bilhetes.
Estou tentando comparar o custo de substituir uma geladeira antiga agora para economizar na conta de luz, em vez de esperar até que ela quebre para substituí-la. Consigo calcular quanto mais barato é usar a geladeira nova em comparação com a antiga: US$ 37 por ano, fácil. Mas como levo em conta o custo da geladeira nova? Digamos que ela custe US$ 425. Não posso dizer que *todos* esses US$ 425 sejam uma despesa nova, porque terei que substituir a geladeira antiga *algum dia*, se não agora, então terei essa despesa com a geladeira nova em algum momento de qualquer maneira. Digamos que uma geladeira típica dure 14 anos e a minha antiga tenha 9 anos, então, se eu a substituísse agora, teria que substituí-la em 5 anos. Tentei criar uma tabela de duas colunas, comparando o custo de manter a geladeira atual por 9 anos e depois substituí-la, versus substituí-la agora, mas não soube como fazer uma comparação justa, pois não sabia por quanto tempo considerar os custos e porque as geladeiras são substituídas em anos diferentes. Como posso comparar a economia de substituir agora versus substituir mais tarde? Aliás, isso não é para a minha situação, porque minha geladeira atual provavelmente tem 30 anos. É para, hum, um amigo.
Se você mantiver a geladeira atual, em cinco anos terá gasto US$ 37 * 5 = US$ 185 a mais em eletricidade em comparação com uma nova. Se você a substituir agora, gastará US$ 425, mas, considerando a depreciação linear, após cinco anos ela ainda valerá US$ 425 * (9/14) = US$ 273,21. Portanto, você terá perdido US$ 425 * (5/14) = US$ 151,79 devido à depreciação. Assim, o custo da depreciação da nova geladeira é menor do que a despesa adicional com eletricidade ao manter a antiga, então eu prefiro comprar uma nova agora.
Se houver três pessoas, qual é a probabilidade de que pelo menos duas delas façam aniversário na mesma data?
Desconsiderando o dia bissexto, a probabilidade de haver três aniversários diferentes é (364/365)*(363/365) = 0,99179583. Portanto, a probabilidade de haver pelo menos um aniversário em comum é 1 - 0,99179583 = 0,00820417.
Cinco pessoas estão em uma sala. Qual é a probabilidade de que pelo menos duas delas tenham nascido no mesmo mês?
Para simplificar, vamos assumir que cada pessoa tem 1/12 de probabilidade de nascer em cada mês. A probabilidade de todas as cinco pessoas nascerem em meses diferentes é (11/12)*(10/12)*(9/12)*(8/12) = 0,381944. Portanto, a probabilidade de nascerem em um mesmo mês é 1 - 0,381944 = 0,618056.
Recebemos um desafio no trabalho — só por diversão — e ninguém consegue resolvê-lo. Um fazendeiro tem 5 caminhões cheios de ovelhas. Quatro dos caminhões contêm ovelhas com 39 kg e o quinto caminhão contém ovelhas com 40 kg. Todas as ovelhas são idênticas. Ele vai ao mercado. Ele quer descobrir qual dos caminhões contém a ovelha de 40 kg, e ele só pode usar a balança grande uma vez!!! Como ele vai fazer isso? Por favor, ajudem, isso está nos deixando todos loucos no meu trabalho — é uma clínica veterinária!!
A resposta está no final da coluna.
Resposta à pergunta sobre ovelhas
Pegue uma ovelha do reboque 1, duas do reboque 2, três do reboque 3, quatro do reboque 4 e nenhuma do reboque 5. Se todas as ovelhas pesassem 39 kg, o peso total seria 39 * 10 = 390 kg. No entanto, as ovelhas de 0 a 4 pesam um quilo a mais. Se o peso total for 391 kg, então há uma ovelha pesada na balança; portanto, ela deve ter vindo do reboque 1. Da mesma forma, se o peso total for 392 kg, então há duas ovelhas pesadas na balança, que devem ter vindo do reboque 2. Assim também, um peso de 393 kg significa que as ovelhas pesadas estão no reboque 3, um peso de 394 kg significa que as ovelhas pesadas estão no reboque 4 e um peso de 390 kg significa que as ovelhas pesadas estão no reboque 5.
Em um avião com 180 lugares, qual a probabilidade de eu sentar ao lado daquela garota bonita que eu vi e que estará no mesmo voo?
Depende do número de assentos em um grupo. A maioria dos voos domésticos tem três assentos de cada lado do corredor. Isso resultaria em 60 grupos de 3 assentos. Depois que o primeiro de vocês estiver sentado, haverá dois assentos no mesmo grupo dos 179 restantes, então a probabilidade de estarem no mesmo grupo é de 2/179 = 1,12%. Além disso, não pode haver outra pessoa no assento do meio. A probabilidade de a terceira pessoa estar no assento do meio é de 1/3. Portanto, a resposta é (2/179)*(2/3) = 0,74%, ou 1 em 134,25.
Três lógicos estão jogando um jogo. Cada um deve anotar secretamente um número inteiro positivo. O lógico com o menor número inteiro único ganhará $3. Se os três tiverem o mesmo número, cada um ganhará $1. Os lógicos são egoístas e cada um deseja maximizar seus próprios ganhos. A comunicação entre eles não é permitida. Qual estratégia cada lógico seguirá?
A resposta aparecerá na próxima coluna.
Normalmente, eu diria que isso está fora da minha área de especialização. No entanto, como ex-atuário do governo por oito anos, entendo um pouco de impostos. Pelo que li, a maior parte da renda de Warren Buffett é definida como ganho de capital, que é tributado a uma taxa de apenas 15%. Gostemos ou não, as leis tributárias permitem isso. O que me intrigou foi o fato de sua secretária estar pagando 30%. De acordo com este vídeo , ele estava contabilizando "impostos sobre a folha de pagamento e sobre a renda". Por "impostos sobre a folha de pagamento", ele obviamente se referia aos impostos da Previdência Social e do Medicare. Vamos ver se 30% é uma alíquota razoável de imposto federal total para sua secretária.
Em 2007, a alíquota máxima do imposto de renda era de 35%, mas isso se aplicava apenas à renda acima de US$ 349.700. A renda até esse valor era tributada com uma alíquota muito menor. Suponhamos que a secretária dele seja solteira, sem filhos dependentes, e que seu salário fosse de US$ 100.000. Primeiro, vamos subtrair as deduções mínimas. Em 2007, a dedução padrão para contribuintes solteiros era de US$ 5.350. A dedução pessoal era de US$ 3.400. Assim, restam US$ 100.000 - US$ 5.350 - US$ 3.400 = US$ 91.250 de renda sujeita ao imposto de renda. Para contribuintes solteiros em 2007, a alíquota era de 10% sobre os primeiros US$ 7.825 de renda, depois 15% até US$ 31.850, 25% até US$ 77.100 e 28% até US$ 160.850. Portanto, o imposto de renda dela teria sido de = 0,1 × $7.825 + 0,15 × ($31.850 - $7.825) + 0,25 × ($77.100 - $31.850) + 0,28 × ($91.250 - $77.100) = $19.660,75. Isso representa apenas 19,7% da renda dela. Todas as minhas suposições, como a renda dela, o tipo de declaração e o fato de ela não ter optado pela declaração detalhada, contribuíram para uma alíquota de imposto mais alta.
Agora vamos falar sobre a Previdência Social e o Medicare. Em 2007, a contribuição para a Previdência Social era de 6,2%, até uma renda de US$ 97.500, quando a isenção era total. A alíquota do Medicare em 2007 era de 1,45%, sem limite máximo. Portanto, a soma das contribuições para a Previdência Social e o Medicare seria de 6,2% * 97.500 + 1,45% * 100.000 = US$ 7.495. Considerando esses impostos, a alíquota total seria de (US$ 19.660,75 + US$ 7.495) / US$ 100.000 = 27,2%. Mesmo assim, faltam 2,8% para atingir os 30%.
Meu palpite é que ela também esteja considerando o fato de que, no fim das contas, é ela quem paga a contribuição previdenciária e o Medicare que cabem ao empregador. Para quem não sabe, as contribuições previdenciárias e do Medicare são, na verdade, o dobro do valor descontado do salário. O empregador paga a outra metade. No entanto, alguns, inclusive eu, argumentariam que, no fim das contas, é o empregado quem paga ambas as contribuições. Se o empregador não tivesse que pagar esse imposto, teria mais dinheiro para pagar seus funcionários. É fácil pensar assim quando se é autônomo, como eu, e se tem que pagar as duas partes. Se dobrarmos a contribuição previdenciária/do Medicare, a alíquota passa a ser ($19.660,75 + 2 × $7.495) / $100.000 = 34,7%. Presumo que a diferença de 4,7% se deva ao fato de ela ganhar menos de $100.000, ser casada, ter dependentes, optar pela declaração detalhada de deduções ou alguma combinação desses fatores.
Os impostos da Previdência Social e do Medicare não teriam grande impacto sobre Warren Buffett. Primeiro, o teto de US$ 97.500 para a Previdência Social seria insignificante para ele. Segundo, esses impostos incidem sobre salários, não sobre ganhos de capital, como ele define a maior parte de sua renda.
Então, essa é a minha melhor hipótese quanto ao raciocínio matemático por trás da declaração do Sr. Buffett.
Atualização: Pouco depois da publicação desta coluna, recebi a seguinte resposta. Em prol da imparcialidade, apresento o seguinte argumento de que o Sr. Buffett está pagando impostos em excesso.
Li com interesse sua resposta à pessoa "indignada" que considera injusto que Warren Buffett pague uma porcentagem menor de impostos do que sua secretária. Fiquei decepcionado com sua resposta, que não corrige a informação errônea que dá a entender que o Sr. Buffett paga menos impostos do que sua secretária.Primeiro, como você observou, a renda de investimentos é de fato tributada em 15%. Isso, na prática, configura dupla tributação, já que a renda do trabalho que o Sr. Buffett investiu foi tributada à sua alíquota marginal de 36%. É como comparar alhos com bugalhos (renda do trabalho versus renda de investimentos).
Em segundo lugar, não se deve olhar para a porcentagem. Em termos de jogos de azar, deve-se olhar para o "pagamento". Tenho quase certeza de que o Sr. Buffett pagou milhões de dólares em impostos no mesmo ano em que sua secretária pagou milhares de dólares.O leitor não deveria ficar mais indignado com o fato de um cidadão do país pagar milhares de vezes mais do que outros cidadãos pelos mesmos serviços governamentais? Poderíamos igualmente dizer: "Ouvi dizer que Warren Buffett pagou 1.000.000 vezes mais impostos do que sua secretária, isso é um absurdo!"
Só queria salientar que analisar apenas a "porcentagem" e não o "pagamento real" é uma falácia. Semelhante a muitas das suas falácias sobre jogos de azar .
Atenciosamente,
Kevin A. (Dallas)
Obrigado pela sua divertida coleção de quebra-cabeças matemáticos. Minha namorada e eu criamos esta variação do quebra-cabeça dos piratas. E se todos os piratas tivessem a mesma patente e, em cada rodada, o proponente da divisão fosse escolhido por sorteio? Nesta variação, suponha que a maior prioridade de cada pirata seja maximizar a quantidade esperada de moedas recebidas. Eu acho que tenho a solução, mas talvez você queira tentar primeiro. Obrigado novamente.
De nada. Se restarem apenas dois piratas, aquele escolhido para dar uma sugestão não terá chance, pois o outro votará contra. O sorteado receberá zero, e o outro, todas as 1000 moedas. Portanto, antes do sorteio, o valor esperado com dois piratas restantes é de 500 moedas.
Na fase dos três piratas, o pirata sorteado deve sugerir dar 501 moedas a um dos outros piratas e 499 moedas a si mesmo. Aquele que receber 501 moedas votará sim, pois é mais do que o valor esperado de 500 ao votar não. Antes do sorteio, com três piratas restantes, cada um tem 1/3 de chance de receber 0, 499 ou 501 moedas, resultando em uma média de 333,33.
Na fase dos quatro piratas, o pirata sorteado deve escolher dar 334 moedas para quaisquer dois dos outros piratas e 332 para si mesmo. Isso lhe renderá dois votos "sim" dos piratas que receberiam 334 moedas, pois eles prefeririam 334 a 333,33. Incluindo o seu próprio voto, você terá 3 de 4 votos. Antes do sorteio, o valor esperado para cada pirata é a média de 0, 334, 334 e 332, ou 1000/4 = 250.
Pela mesma lógica, na fase dos cinco piratas, o pirata sorteado deve escolher dar 251 moedas para quaisquer dois piratas e 498 moedas para si mesmo. Ao contrário do problema original, não é necessário fazer o cálculo inverso. Basta dividir o número de moedas pelo número de piratas, sem incluir você. Em seguida, dê a metade deles (arredondando para baixo) essa média, mais uma moeda.
Preciso de ajuda com um enigma chamado Eternity II. O prêmio para quem o resolver é de impressionantes US$ 2.000.000, uma quantia considerável para mim. Aqui está um link para uma entrevista, incluindo o próprio criador do jogo, Christopher Monckton (ex-conselheiro de Margaret Thatcher, entre outras coisas). O jogo obviamente não tem nada a ver com apostas, mas, apesar disso, talvez você pudesse adicionar uma ou duas palavras sobre ele na sua página da web.
O criador do jogo se gaba de que o enigma é insolúvel, no link acima. Estou começando a achar que ele está certo e que ele mesmo será o único que ficará rico vendendo esse jogo (ridículo, mas fascinante). Como você, sendo matemático, resolveria esse tipo de enigma?
Espero que você esteja feliz; eu fiquei obcecado por esse quebra-cabeça no último mês. Tive sorte (ou talvez azar) de encontrar o quebra-cabeça de 256 peças na livraria Borders aqui perto, mas precisei comprar os quatro quebra-cabeças com dicas no eBay, de um cara na Austrália.
Criei um programa que resolve facilmente os quatro quebra-cabeças de pistas. Ele resolveu o quebra-cabeça de pistas nº 4, com 72 peças, em menos de um segundo. Usei um programa recursivo de força bruta simples. Tracei um caminho no tabuleiro, começando pela borda. Em cada posição, o programa percorria todas as peças não utilizadas, procurando uma que se encaixasse. Se encontrasse uma, avançava para a próxima casa; caso contrário, retrocedia uma casa.
Tenho dois computadores trabalhando incansavelmente no quebra-cabeça de 256 peças, avaliado em 2 milhões de dólares, há semanas, e nenhum deles chegou perto. Concordo com o que o criador disse naquele vídeo: mesmo que conectássemos dez milhões dos computadores mais rápidos do mundo, talvez eles não encontrassem a solução até o fim do universo. Você pensaria que eu teria dado ouvidos ao aviso dele antes de começar, mas diante de um bom quebra-cabeça, toda a consideração pelo uso prático do meu tempo desaparece.
Tenho várias ideias para atalhos, mas mesmo que acelerassem meu programa em um bilhão de vezes, provavelmente não ajudaria. Ficaria extremamente impressionado se alguém resolvesse isso. O que realmente me incomoda é que sinto que existe algum ramo desconhecido da matemática que poderia resolver quebra-cabeças como esse facilmente. Até lá, acho que a tentativa e erro glorificada é o melhor que podemos fazer para resolvê-lo. Os computadores de hoje são simplesmente lentos demais, e o número de combinações é vasto demais, para que isso tenha alguma chance de sucesso.

Suponha que a distância entre duas cidades seja de 1000 milhas. Sem vento, um avião pode viajar a 500 mph. Levará mais tempo para fazer a viagem de ida e volta sem vento ou com um vento de cauda direto de 100 mph em uma direção e um vento de proa igual na direção oposta?
Sem vento, a viagem levará 2 horas em cada sentido, totalizando 4 horas. Com vento de cauda, o avião viajará a 600 mph, fazendo a viagem em 1000/600 = 1,667 horas. Com vento de proa, o avião viajará a 400 mph, levando 1000/400 = 2,5 horas. Portanto, com vento, o tempo total será de 4,167 horas, ou seja, 10 minutos a mais.
Isso só demonstra como é perigoso fazer médias. Não se pode dizer que a velocidade média de uma viagem é de 500 mph se ela for de 400 mph em um trecho e 600 mph no outro, porque o trecho de 400 mph dura mais tempo.
Se isso não for intuitivo, imagine um vento de 800 km/h. O avião levaria apenas 1 hora com o vento a favor, mas ficaria parado no mesmo lugar na direção oposta, levando uma eternidade.
Recentemente, participei de um sorteio com 7.033 prêmios e a probabilidade de ganhar é de 1 em 13. Comprei 5 bilhetes. Qual é a minha probabilidade real de ganhar algo? Além disso, há 40 prêmios principais. Qual é a minha probabilidade de ganhar um prêmio principal?
Para simplificar, vamos ignorar o fato de que, quanto mais bilhetes você compra, menor se torna o valor de cada bilhete, pois você está competindo consigo mesmo. Dito isso, a probabilidade de perder todos os cinco bilhetes é (12/13) 5 = 67,02%. Portanto, a probabilidade de ganhar pelo menos um prêmio é de 32,98%. Há um total de 7033 × 13 = 91.429 bilhetes no tambor antes de você comprar qualquer um. 91.429 - 40 = 91.389 não são prêmios grandes. A probabilidade de não ganhar nenhum prêmio grande com cinco bilhetes é (91.389/91.429) 5 = 99,78%. Portanto, a probabilidade de ganhar pelo menos um prêmio grande é de 0,22%, ou 1 em 458.
Tenho um enigma que tento resolver há alguns meses, sem qualquer progresso. Se tiver tempo, espero que possa me ajudar, pois tem me tirado o sono :-). Enfim, no glossário de Beyond Counting -- Exhibit CAA , três sequências de números e letras são apresentadas como verbete para "Números Mágicos". Um desses números inclusive estampa a capa do livro, então presumo que tenham alguma importância. Você tem alguma ideia?
Não costumo dizer isso, mas não faço ideia. Como você mencionou em outro e-mail, elas seguem o formato do número de série das notas de dólar: duas letras, com um número de dez dígitos entre elas. Por respeito aos direitos autorais, não vou revelar quais são os números aqui.
Tenho curiosidade em saber o que aconteceu com o desafio do quebra-cabeça de Eternity II. Foi resolvido? Você ainda está trabalhando nele?
Obrigado por perguntar. Não, não mexi nesse assunto desde que escrevi sobre ele na coluna "Pergunte ao Mago" de 17 de novembro de 2008. De acordo com o site deles, haverá "datas de análise" em 31 de dezembro de 2009 e, se necessário, em 2010. Na minha opinião, isso nunca será resolvido.
Atualização: Aparentemente, o site Eternity II não existe mais.
Li com fascínio o post do Wizard sobre a carta de veto de Arnold Schwarzenegger. Minha pergunta diz respeito à resposta ridícula, porém previsível, do governador. Ele afirmou que foi apenas uma "mera coincidência". Apesar das inúmeras evidências circunstanciais (o autor do projeto de lei e destinatário da carta era a mesma pessoa que havia insultado o governador uma semana antes), você teria alguma estimativa da probabilidade de uma carta de exatamente sete linhas soletrar essa frase por acaso? Acredito que, levando em conta as letras utilizadas, a probabilidade será ainda maior do que atribuir uma chance de 1 em 26 para cada uma. Não me parece que U, Y e, principalmente, K sejam letras comuns no início de palavras.
Se você se ofende facilmente, por favor, passe para a próxima pergunta.
Para benefício dos meus leitores que não leram aquele blog, observem a primeira letra de cada linha neste memorando do governador da Califórnia, Arnold Schwarzenegger (PDF) , começando pela linha que inicia com a letra F.
Isso foi discutido no meu site complementar, Wizard of Vegas . Para encontrar uma resposta, consultei a frequência de cada letra inicial das palavras em inglês na Wikipédia .
Frequência de palavras por primeira letra
| Carta | Freqüência |
| UM | 11,60% |
| B | 4,70% |
| C | 3,51% |
| D | 2,67% |
| E | 2,00% |
| F | 3,78% |
| G | 1,95% |
| H | 7,23% |
| EU | 6,29% |
| J | 0,63% |
| K | 0,69% |
| eu | 2,71% |
| M | 4,37% |
| N | 2,37% |
| O | 6,26% |
| P | 2,55% |
| P | 0,17% |
| R | 1,65% |
| S | 7,76% |
| T | 16,67% |
| Você | 1,49% |
| V | 0,62% |
| C | 6,66% |
| X | 0,01% |
| Y | 1,62% |
| Z | 0,05% |
Para estimar a probabilidade de que a mensagem de Arnold fosse de fato apenas uma coincidência, teríamos Prob(F) × Prob(U) × ... × prob(U) = 0,0378 × 0,0149 × 0,0351 × 0,0069 × 0,0162 × 0,0626 × 0,0149 = 1 em 486.804.391.348. Isso nem sequer leva em consideração o fato de que uma quebra de linha convenientemente estava no lugar do espaço entre as duas palavras.
Gostaria de agradecer a Eliot J. e Jonathan F. por suas contribuições para esta solução.
Na esteira de bagagens do aeroporto, quanto mais malas eu tiver para pegar, mais tempo terei que esperar até que todas elas apareçam. Se eu tiver apenas uma mala, terei que esperar até que cerca de metade das malas apareçam. Se eu tiver duas malas, a espera será maior e com três, ainda maior. Supondo que minhas malas sejam misturadas aleatoriamente com as outras, qual é uma fórmula geral para calcular quantas malas terei que esperar até que todas as minhas apareçam, em função do número de malas que tenho e do número total de malas?
Vamos definir algumas variáveis primeiro, da seguinte forma:
n = número de suas malas
b = número total de sacos
À medida que o número total de malas aumenta, a resposta se aproxima de b×n/(n+1). Para um avião grande, isso lhe dará uma boa estimativa. No entanto, se você quiser ser exato, a resposta é
[b× combin (b,n)-(soma para i=n até b-1 de combin(i,n))]/combin(b,n)
Por exemplo, se houver um total de 10 malas e quatro delas forem suas, o tempo de espera previsto será de =
[10×combin(10,4)-combin(4,4)-combin(5,4)-combin(6,4)-combin(7,4)-combin(8,4)-combin(9,4)]/combin(10,4) = 8,8 sacos.
Solução:
O número de maneiras de escolher n sacos dentre b sacos é combin(b,n). Portanto, a probabilidade de que todos os seus sacos sejam retirados entre os primeiros x sacos é combin(x,n)/combin(b,n). A probabilidade de que seu último saco seja o x- ésimo saco a ser retirado é (combin(x,n)-combin(x-1,n))/combin(b,n), para x>=n+1. Para x=n, é 1/combin(b,n).
Assim, a proporção entre o tempo de espera previsto e o tempo de espera total é:
n×combin(n,n)/combin(b,n) +
(n+1)×(combinar(n+1,n)-combinar(n,n))/combinar(b,n) +
(n+2)×(combinar(n+2,n)-combinar(n+1,n))/combinar(b,n) +
.
.
.
+
(b-1)×(combinar(b-1,n)-combinar(b-2,n))/combinar(b,n) +
b×(combinar(b,n)-combinar(b-1,n))/combinar(b,n)
Fazendo uma soma telescópica, isso pode ser simplificado para:
[b×combin(b,n)-combin(b-1,n)-combin(b-2,n)-...-combin(n,n)]/combin(b,n)
Um leitor escreveu mais tarde dizendo que a resposta pode ser simplificada para n×(b+1)/(n+1). Isso pode ser demonstrado por indução, um método legítimo, mas sempre me deixa emocionalmente insatisfeito.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Eu vendo esculturas. Em média, de cada sete vendas, uma é de uma tartaruga e as demais são de outros tipos. Quantas tartarugas eu preciso ter em estoque para ter 90% de chance de não ficar sem nas próximas 100 vendas?

Seja t o número de tartarugas produzidas e x o número de tartarugas vendidas.
pr(x<=t)=0,9
pr(x-14,29<=t-14,29)=0,9
pr((x-14,29)/3,5)<=(t-14,29)/3,5))=0,9
O lado esquerdo da desigualdade segue uma distribuição normal padrão (média de 0, desvio padrão de 1). Este próximo passo exige um curso introdutório de estatística, ou alguma fé, para ser aceito.
(t-14,29)/3,5 = normsinv(0,9) Esta é a função do Excel.
(t-14,29)/3,5 = 1,282
t-14,29 = 4,4870
t = 18,77
É improvável que alguém compre 0,77 de uma estátua de tartaruga, então eu arredondaria para 19. De acordo com a distribuição binomial, a probabilidade de vender 18 ou menos é de 88,35%, e 19 ou menos é de 92,74%. Essa questão foi levantada e discutida no fórum do meu site parceiro, Wizard of Vegas .
Cinco marinheiros sobrevivem a um naufrágio. A primeira coisa que fazem é recolher cocos e colocá-los em uma grande pilha comunitária. Pretendiam dividi-los igualmente depois, mas, após o árduo trabalho de recolher os cocos, estão muito cansados. Então, vão dormir, planejando dividir a pilha pela manhã.
No entanto, os marinheiros não confiam uns nos outros. À meia-noite, um deles acorda para pegar sua parte. Ele divide a pilha em cinco partes iguais, sobrando um coco. Ele enterra sua parte, junta as outras quatro pilhas em uma nova pilha comunitária e dá o coco restante a um macaco.
À 1h, 2h, 3h e 4h da manhã, cada um dos outros quatro marinheiros faz exatamente a mesma coisa.
De manhã, ninguém confessa o que fez, e eles prosseguem com o plano original de dividir a pilha igualmente. Novamente, sobra um coco, que eles dão ao macaco.
Qual é o menor número possível de cocos na pilha original?
"Role a página 100 linhas para baixo para ver a resposta."
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
Havia 15.621 cocos na pilha original. Desça mais 100 linhas para ver minha solução.
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
Seja c o número de cocos na pilha original e f a parte final para cada marinheiro após a última divisão.
Depois que o marinheiro 1 pegar sua parte e der seu coco ao macaco, restarão (4/5)×(c-1) = (4c-1)/5.
Depois que o marinheiro 2 pegar sua parte e der seu coco ao macaco, restarão (4/5)×(((4c-1)/5)-1) = (16c-36)/25.
Depois que o marinheiro 3 pegar sua parte e der seu coco ao macaco, restarão (4/5)×(((16c-36)/25)-1) = (64c-244)/125.
Depois que o marinheiro 4 pegar sua parte e der seu coco ao macaco, restarão (4/5)×(((64c-244)/125)-1) = (256c-1476)/625.
Depois que o marinheiro 5 pegar sua parte e der seu coco ao macaco, restarão (4/5)×(((256c-1476)/625)-1) = (1024c-8404)/3125.
Pela manhã, a parte de cada marinheiro da pilha restante será f = (1/5)×(((1024c-8404)/3125)-1) = (1024c-11529)/15625 restantes.
Então, a questão é qual o menor valor de c tal que f=(1024×c-11529)/15625 seja um número inteiro. Vamos expressar c em termos de f.
(1024×c-11529)/15625 = f
1024c - 11529 = 15625×f
1024c = 15625f + 11529
c = (15625f+11529)/1024
c = 11+((15625×f+265)/1024)
c = 11+15×f+(265×(f+1))/1024
Então, qual é o menor valor de f tal que 265×(f+1)/1024 seja um número inteiro? 265 e 1024 não têm fatores comuns, então f+1 por si só precisa ser divisível por 1024. O menor valor possível para f+1 é 1024, então f=1023.
Assim, c = (15625×1023+11529)/1024 = 15.621.
Eis a quantidade de cocos que cada pessoa, e cada macaco, receberam:
Problema do coco
| Marinheiro | Cocos |
| 1 | 4147 |
| 2 | 3522 |
| 3 | 3022 |
| 4 | 2622 |
| 5 | 2302 |
| Macaco | 6 |
| Total | 15621 |
David Filmer, que me desafiou com a pergunta, já sabia a resposta. Na verdade, ele me perguntou a fórmula para o caso geral de s marinheiros, mas eu tive bastante dificuldade com o caso específico de 5 marinheiros. David observou que a resposta para o caso geral é c = s s+1 - s + 1.
Deixo essa comprovação para o leitor.
Aqui estão alguns links para soluções alternativas para o problema:
Um homem recebe dois envelopes cheios de dinheiro. Um dos envelopes contém o dobro da quantia do outro. Depois de escolher seu envelope, abri-lo e contar o dinheiro, ele tem a opção de trocá-lo pelo outro. A questão é: o homem ganha alguma coisa ao trocar o envelope?
Ao que tudo indica, ao trocar o envelope, o homem teria 50% de chance de dobrar seu dinheiro caso o envelope inicial contivesse o menor valor, e 50% de chance de reduzi-lo à metade caso o envelope inicial contivesse o maior valor. Portanto, seja x o valor contido no envelope inicial e y o valor da troca:
y = 0,5×(x/2) + 0,5×(2x) = 1,25x
Vamos supor que o envelope inicial continha US$ 100. Portanto, deve haver 50% de chance de que o outro envelope contenha 2 × US$ 100 = US$ 200 e 50% de chance de que o terceiro envelope contenha (1/2) × US$ 100 = US$ 50. Nesse caso, o valor do envelope é:
0,5 × ($100/2) + 0,5 × (2 × $100) = $125
Isso implica que o homem aumentaria, em média, sua riqueza em 25% simplesmente trocando os envelopes! Como isso é possível?
Isso parece ser um paradoxo matemático, mas na verdade é apenas um abuso da fórmula do valor esperado. Como você observou na pergunta, parece que o outro envelope deveria ter 25% a mais do que o que você escolheu. No entanto, se você aceitar isso, então poderia muito bem escolher o outro envelope desde o início. Além disso, você poderia usar esse argumento para ficar alternando entre os envelopes indefinidamente, caso não consiga abri-los antes de decidir trocar. Claramente, deve haver alguma falha no argumento do valor esperado. A questão é: onde está a falha?
Passei muito tempo lendo e discutindo sobre esse problema ao longo dos anos. Ouvi e li muitas explicações sobre por que o argumento y = 0,5x + 0,5 * 2x = 1,25x está errado. Muitos usaram páginas e páginas de matemática avançada na explicação, o que não acho necessário. É uma questão simples que exige uma resposta simples. Então, esta é a minha tentativa.
Você deve ter muito cuidado com o que fizer com a informação de que um envelope contém o dobro do dinheiro do outro. Vamos chamar a quantia no envelope menor de S e a do envelope maior de L. Assim, temos:
L=2×S
S=0,5×L
Observe como os fatores 2 e 0,5 são aplicados a envelopes diferentes . Você não pode pegar ambos os fatores e aplicá-los ao mesmo valor. Se o primeiro envelope tiver $100, então, se for o envelope menor, o outro terá $200. Se o envelope de $100 for o maior, então o outro terá $50. Portanto, o outro envelope terá $50 ou $200. No entanto, você não pode concluir que há 50% de chance para cada um. Isso porque seria aplicar os fatores 0,5 e 2 ao mesmo valor, o que não é possível. Sem saber a distribuição dos prêmios inicialmente, você não pode atribuir valores possíveis ao segundo envelope.
Se o argumento 0,5x/2x estiver errado, qual seria a maneira correta de definir o valor esperado do outro envelope? Eu faria da seguinte forma: a diferença entre os dois envelopes é LS = 2S - S = S. Ao trocar de envelope, você ganhará ou perderá S, seja qual for o valor. Se os dois envelopes tiverem $50 e $100, a troca resultará em um ganho ou perda de $50. Se os dois envelopes tiverem $100 e $200, a troca resultará em um ganho ou perda de $100. De qualquer forma, o ganho esperado com a troca é 0. Acho que poderia dizer que, se o primeiro envelope tiver $100, há 50% de chance de a diferença no outro envelope ser de $50 e 50% de chance de ser de $100. Portanto, a diferença esperada é de $75. Assim, o valor esperado do outro envelope é 0,5×($100+$75) + 0,5×($100-$75) = 0,5×($175+$25) = $100.
Espero que isso faça algum sentido. Esse problema sempre gera muitos comentários. Se você tiver algum, por favor, não me escreva diretamente, mas poste no meu fórum do Wizard of Vegas. O link está abaixo.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Ligações
Considere um truel (um duelo triplo) com os participantes A, B e C. Eles estão lutando até a morte por uma mulher. Todos são cavalheiros e concordam com as seguintes regras.
- Os três participantes formam um triângulo.
- Cada um possui apenas uma bala.
- Primeiro vai A, depois B e, por último, C.
- A probabilidade de A atingir o alvo pretendido é de 10%.
- A probabilidade de B atingir o alvo pretendido é de 60%.
- A probabilidade de C acertar o alvo pretendido é de 90%.
- Não existem disparos acidentais.
- Atirar para o ar (errando de propósito) e atirar em si mesmo são permitidos e sempre dão certo.
- Se restarem dois ou três sobreviventes após qualquer rodada, cada um receberá uma nova bala. Eles então repetirão o processo, atirando alternadamente, na mesma ordem, ignorando qualquer um que já tenha morrido.
- Os três participantes são excelentes lógicos.
Em quem A deve mirar inicialmente? Qual é a probabilidade de sobrevivência dele para cada alvo inicial?
Este enigma é discutido no programa da BBC "Quite Interesting" . Desça 100 linhas para ver a resposta e a solução.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
Aqui estão as minhas probabilidades de A vencer de acordo com cada alvo inicial. Como você pode ver, a probabilidade de A vencer é maximizada atirando deliberadamente para o ar.
Probabilidades Verdadeiras
| Estratégia | Prob. Vitória |
| Ar | 13,887% |
| UM | 0,000% |
| B | 12,560% |
| C | 13,094% |
Para a solução, vamos usar a notação Pr(X) para denotar a probabilidade de o grupo X, e somente o grupo X, permanecer após uma rodada. Vamos usar a terminologia Pr(X*) para denotar a probabilidade de o grupo X eventualmente vencer a rodada, após repetições até que o estado do jogo mude devido a alguém ser atingido. Seja Pr(X**) a probabilidade de o jogador X ser o único sobrevivente. Para encontrar as probabilidades finais, vamos analisar primeiro os estados com dois jogadores. É óbvio que cada um atirará no outro.
A vs. B
- Pr(A) = 0,1
- Pr(B) = 0,9 × 0,6 = 0,54
- Pr(AB) = 0,9 × 0,4 = 0,36
Se ambos sobreviverem, o processo se repetirá até que reste apenas um sobrevivente. Portanto, as probabilidades de ser o último sobrevivente são:
- Pr(A*) = Pr(A)/(1-Pr(AB)) = 0,1/0,64 = 0,15625
- Pr(B*) = Pr(B)/(1-Pr(AB)) = 0,54/0,64 = 0,84375
A vs. C
- Pr(A) = 0,1
- Pr(C) = 0,9×0,9 = 0,81
- Pr(AC) = 0,9×0,1 = 0,09
Se ambos sobreviverem, o processo se repetirá até que reste apenas um sobrevivente. Portanto, as probabilidades de ser o último sobrevivente são:
- Pr(A*) = Pr(A)/(1-Pr(AC)) = 0,1/0,91 = 0,10989011
- Pr(C*) = Pr(B)/(1-Pr(AC)) = 0,81/0,91= 0,89010989
B vs. C
- Pr(B) = 0,6
- Pr(C) = 0,4 × 0,9 = 0,36
- Pr(BC) = 0,$×0,1 = 0,04
Se ambos sobreviverem, o processo se repetirá até que reste apenas um sobrevivente. Portanto, as probabilidades de ser o último sobrevivente são:
- Pr(B*) = Pr(A)/(1-Pr(BC)) = 0,6/0,96 = 0,625
- Pr(C*) = Pr(B)/(1-Pr(BC)) = 0,36/0,96= 0,375
Agora estamos prontos para analisar o caso com três jogadores. Vamos considerar a situação em que A tem como alvo B.
Três jogadores — A mira em B
Se A atingir B, então C certamente sobreviverá e poderá ou não atingir A. Portanto, dois resultados possíveis de atingir B são AC e C. Se A errar B, então B mirará na ameaça maior, C. Se B atingir C, então A e B sobreviverão. Se B errar C, então C mirará na ameaça maior, B. Se C errar B, então todos os três sobreviverão. Se C atingir B, então A e C sobreviverão. Portanto, os resultados possíveis são C, AB, AC e ABC.
- Pr(A) = 0.
- Pr(B) = 0.
- Pr(C) = 0,1 × 0,9 = 0,09. Isso é alcançado por A atingindo B e, em seguida, C atingindo A.
- Pr(AB) = 0,9 × 0,6 = 0,54. Isso é conseguido por A não atingir B e, em seguida, B atingir C.
- Pr(AC) = 0,1 × 0,1 + 0,9 × 0,4 × 0,9 = 0,334. Isso pode ser alcançado de duas maneiras. A primeira é A acertando B e, em seguida, C errando A. A segunda é A errando B, B errando C e, em seguida, C acertando B.
- Pr(BC) = 0.
- Pr(ABC) = 0,9 × 0,4 × 0,1 = 0,036. Isso é alcançado por todos os três elementos faltantes.
Pela mesma lógica dos casos de dois jogadores, podemos dividir cada resultado por (1-Pr(ABC))=0,964 para encontrar as probabilidades de cada estado, assumindo que o estado do jogo mudou após a rodada.
- Pr(C*) = 0,09/0,964 = 0,093361.
- Pr(AB*) = 0,54/0,964 = 0,560166.
- Pr(AC*) = 0,334/0,964 = 0,346473.
Nos casos com dois jogadores, sabemos que se restarem apenas A e B, A vencerá com probabilidade de 0,15625 e B com probabilidade de 0,84375. Se restarem apenas A e C, A vencerá com probabilidade de 0,109890 e C com probabilidade de 0,890110.
- Pr(A**) = (0,560165975 × 0,15625) + (0,346473029 × 0,10989011) = 0,125600. A pode ser o vencedor de duas maneiras: (1) chegando ao estado AB e então vencendo, ou (2) chegando ao estado AC e então vencendo.
- Pr(B**) = 0,560166 × 0,84375 = 0,472640. B será o vencedor se chegar ao estado AB, e então B vence.
- Pr(C**) = 0,093361 + (0,346473 × 0,890110) = 0,401760. C pode vencer se A matar B e depois C matar A na primeira rodada, ou se chegar ao estado AC e então C vencer.
Assim, se a estratégia de A for atacar B primeiro, sua probabilidade de ser o único sobrevivente é de 12,56%.
Três jogadores — A mira em C
Se A atingir C, então B certamente sobreviverá e poderá ou não atingir A. Portanto, dois resultados possíveis ao atingir C são AB e B. Se A errar C, então B mirará na ameaça maior, C. Se B atingir C, então A e B sobreviverão. Se B errar C, então C mirará na ameaça maior, B. Se C errar B, então os três sobreviverão. Se C atingir B, então A e C sobreviverão. Assim, os resultados possíveis são B, AB, AC e ABC.
- Pr(A) = 0.
- Pr(B) = 0,1 × 0,6 = 0,06.
- Pr(C) = 0.
- Pr(AB) = (0,1 × 0,4) + (0,9 × 0,6) = 0,04 + 0,54 = 0,58. Isso pode ser obtido de duas maneiras.A primeira situação é A acertando C e, em seguida, B errando A. A segunda situação é A errando B e, em seguida, B acertando C.
- Pr(AC) = 0,9 × 0,4 × 0,9 = 0,324. Isso é alcançado por A errando C, B errando C e C atingindo B.
- Pr(BC) = 0.
- Pr(ABC) = 0,9 × 0,4 × 0,1 = 0,036. Isso é alcançado por todos os três elementos faltantes.
Pela mesma lógica dos casos de dois jogadores, podemos dividir cada resultado por (1-Pr(ABC))=0,964 para encontrar as probabilidades de cada estado, assumindo que o estado do jogo mudou após a rodada.
- Pr(B*) = 0,06/0,964 = 0,062241.
- Pr(AB*) = 0,58/0,964 = 0,601660.
- Pr(AC*) = 0,324/0,964 = 0,336100.
Seguindo a mesma lógica da solução para o caso A visa B:
- Pr(A**) = (0,601660 × 0,15625) + (0,336100 × 0,10989011) = 0,130943.
- Pr(B**) = 0,062241 + 0,601660 × 0,84375 = 0,569891.
- Pr(C**) = 0,336100 × 0,890110 = 0,299166.
Assim, se a estratégia de A for atacar C primeiro, sua probabilidade de ser o único sobrevivente é de 13,09%.
Três jogadores — A erra deliberadamente
Após A errar deliberadamente o alvo, B mirará na ameaça maior, C. Se B acertar C, A e B sobreviverão. Se B errar C, C mirará na ameaça maior, B. Se C errar B, os três sobreviverão. Se C acertar B, A e C sobreviverão. Portanto, os resultados possíveis são AB, AC e ABC.
- Pr(A) = 0.
- Pr(B) = 0.
- Pr(C) = 0.
- Pr(AB) = 0,6. Isso é conseguido quando B atinge C.
- Pr(AC) = 0,4 × 0,9 = 0,36. Isso é conseguido por B errar C e então C atingir B.
- Pr(BC) = 0.
- Pr(ABC) = 0,4 × 0,1 = 0,04. Isso é alcançado por todos os três elementos ausentes.
Pela mesma lógica dos casos de dois jogadores, podemos dividir cada resultado por (1-Pr(ABC))=0,96 para encontrar as probabilidades de cada estado, assumindo que o estado do jogo mudou após a rodada.
- Pr(AB*) = 0,6/0,96 = 0,625.
- Pr(AC*) = 0,36/0,96 = 0,375.
Seguindo a mesma lógica da solução para o caso A visa B:
- Pr(A**) = (0,625 × 0,15625) + (0,375 × 0,109890) = 0,138865.
- Pr(B**) = 0,625 × 0,84375 = 0,527344.
- Pr(C**) = 0,375 × 0,890110 = 0,333791.
Assim, se a estratégia de A for atacar C primeiro, sua probabilidade de ser o único sobrevivente é de 13,89%.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Comparando dois elementos por vez, qual é a maneira mais rápida de ordenar uma lista, minimizando o número máximo de comparações?
Existem várias maneiras igualmente eficazes. No entanto, a que considero mais fácil de entender é chamada de ordenação por intercalação (merge sort) . Veja como funciona:
- Divida a lista em duas. Continue dividindo cada subconjunto em dois, até que todos os subconjuntos tenham tamanho 1 ou 2.
- Ordene cada subconjunto de 2 colocando o elemento menor em primeiro lugar.
- Combine os subconjuntos aos pares. Continue repetindo até que haja apenas uma lista ordenada.
Para mesclar duas listas, compare o primeiro elemento de cada lista e coloque o menor elemento em uma nova lista. Em seguida, repita o processo, colocando o menor elemento após o menor elemento da comparação anterior. Continue repetindo até que os dois grupos sejam mesclados em um único grupo ordenado. Se uma das listas originais estiver vazia, você pode adicionar a outra lista ao final da lista mesclada.
A tabela a seguir mostra o número máximo de comparações necessárias de acordo com o número de elementos na lista.
Mesclar classificação
| Elementos | Comparações máximas |
| 1 | 0 |
| 2 | 1 |
| 4 | 5 |
| 8 | 17 |
| 16 | 49 |
| 32 | 129 |
| 64 | 321 |
| 128 | 769 |
| 256 | 1.793 |
| 512 | 4.097 |
| 1.024 | 9.217 |
| 2.048 | 20.481 |
| 4.096 | 45.057 |
| 8.192 | 98.305 |
| 16.384 | 212.993 |
| 32.768 | 458.753 |
| 65.536 | 983.041 |
| 131.072 | 2.097.153 |
| 262.144 | 4.456.449 |
| 524.288 | 9.437.185 |
| 1.048.576 | 19.922.945 |
| 2.097.152 | 41.943.041 |
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Em 29 de outubro de 2010, o jornal Las Vegas Review Journal publicou uma pesquisa sobre a disputa para o Senado entre Reid e Angle. Segundo a pesquisa, com base em 625 eleitores prováveis, Angle obteve 49% dos votos e Reid, 45%. A pesquisa também informou que a margem de erro era de 4%. Eis as minhas perguntas:
- Qual é a probabilidade de Angle vencer?
- Qual seria o intervalo de confiança de 95% para a porcentagem de votos de Angle?
- O que significa margem de erro?
Peço desculpas pela demora na resposta. Escrevi o seguinte antes da eleição.
Primeiro, vou eliminar os outros 6%, que estão indecisos ou desperdiçarão seus votos em um candidato de um terceiro partido ou em "nenhum dos anteriores", uma opção disponível em Nevada. Alguns podem discordar dessa suposição. Para ser honesto, outro motivo para ignorá-los é que os cálculos se tornam mais complexos com mais de dois candidatos. Assim, após o arredondamento, teríamos 306 votos para Angle e 281 votos para Reid, totalizando 587 na amostra.
Para responder a esta pergunta, vou usar a aproximação da distribuição normal padrão. Se eu fosse perfeccionista, usaria a distribuição t de Student , pois a média e a variância reais não são conhecidas. No entanto, na minha opinião, um tamanho de amostra de 587 é perfeitamente adequado para a distribuição normal.
Tamanho da amostra = 306 + 281 = 587.
A média da amostra de ângulos é 306/587 = 0,521295.
O desvio padrão estimado da média é (0,521295 × 0,478705 / (587-1))^0,5 = 0,0206361.
A participação de Angle acima de 50% é (0,521295-0,5)/0,0206361 = 1,031917 desvios padrão.
De acordo com a distribuição normal, a probabilidade de Reid terminar 1,031917 desvios padrão acima do esperado é 0,151055. Isso pode ser encontrado no Excel com a função DIST.NORM(-1,031917). Portanto, a probabilidade de Angle vencer é 1 - 0,151268 = 84,89%.
Para criar um intervalo de confiança de 95%, observe que o ponto de 2,5% em cada lado da curva gaussiana está a 1,959964 desvios padrão da média. Isso pode ser encontrado no Excel com a função NORMSINV(0,975). Como já mencionado, o desvio padrão estimado da média da amostra é 0,0206361. Portanto, há 95% de chance de que qualquer um dos candidatos fique dentro de 0,0206361 × 1,959964 = 0,040446 desvios padrão dos resultados da pesquisa. Assim, o intervalo de confiança de 95% de Angle é de 0,521295 +/- 0,040446 = 48,08% a 56,17%.
Disseram-me que seria matematicamente incorreto formular isso como "A porcentagem de votos de Angle em relação a todos os votos de Angle/Reid tem 95% de chance de estar entre 48,08% e 56,17%". Foi assim que formulei minha resposta originalmente, mas dois estatísticos se horrorizaram com a minha escolha de palavras. Parafraseando a resposta deles, disseram que eu precisava usar a voz passiva e dizer que "48,08% e 56,17% estarão próximos da porcentagem de votos de Angle com 95% de probabilidade". Para ser sincero, para mim soa igual. No entanto, eles enfatizaram que o intervalo de confiança é aleatório e a porcentagem de votos de Angle é imutável, e que minha formulação original implicava o contrário. De qualquer forma, espero que os estatísticos frequentistas fiquem satisfeitos com a segunda formulação.
A " margem de erro " é metade da diferença entre os dois extremos do intervalo de confiança de 95%. Neste caso, (56,17% - 48,08%)/2 = 4,04%.
Como complemento, aqui estão os resultados reais:
Reid: 361.655
Ângulo: 320.996
Outros: 21.979
Então, sem contar os votos "outros", Reid obteve 53,0% e Angle 47,0%. Isso representa uma vitória confortável de 6% para Reid. Surge então a questão: por que a pesquisa errou tanto? Foi acaso? Os eleitores mudaram de ideia? Ou a pesquisa foi ruim desde o início? Deixo essas perguntas para o leitor (detesto quando livros didáticos dizem isso).
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Tentei usar sua calculadora atuarial. Por que a probabilidade de eu atingir a idade esperada para falecer é inferior a 50%?
Você está confundindo a média com a mediana. Vejamos meu caso como exemplo. Sou um homem de 45 anos. Minha expectativa de vida é de 78,11 anos, mas tenho 50,04% de chance de chegar aos 80 anos.
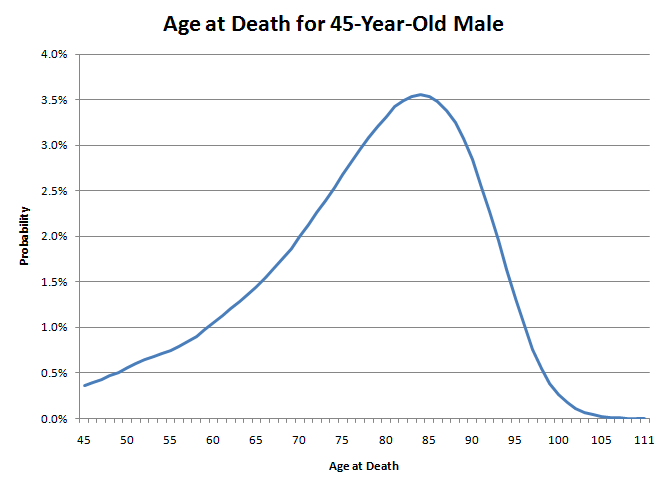
Minha idade de morte será como jogar um dardo neste gráfico. Observe como a cauda esquerda é muito mais espessa que a direita. Isso significa que minha probabilidade de morrer agora é bastante baixa. No entanto, à medida que envelheço, a probabilidade de morrer no próximo ano continuará aumentando. Por exemplo, para um homem de 45 anos, a probabilidade de sobreviver até os 46 é bastante alta, de 99,64%. No entanto, aos 85 anos, a probabilidade de chegar aos 86 é de apenas 89,21%. É como se a natureza estivesse lentamente enfiando uma faca nas suas costas. No início, provavelmente não vai te matar, mas a cada ano que passa, as chances de que isso aconteça aumentam gradualmente. Contudo, quando você chega perto dos setenta anos, a natureza diz chega de brincadeiras e começa a enfiar a faca nas suas costas de verdade.
Portanto, se muitos homens de 45 anos jogassem dardos neste gráfico, 49,96% acertariam entre 45 e 79 anos, e 50,04% acertariam entre 80 e 111 anos. No entanto, a metade sortuda que acerta o lado direito do gráfico provavelmente não viverá muito além dos 80 anos. Depois que um homem chega aos 80 anos, ele pode esperar viver apenas mais 7,78 anos. Enquanto isso, muitos na metade azarada que não chegam aos 80 anos morrerão muito mais jovens. Assim, são as muitas mortes precoces que reduzem a expectativa média de vida.
Para uma situação semelhante, considere um dado numerado 10, 20, 30, 31, 32, 33. A média é 26, mas há 2/3 de chance de rolar um número maior que esse.
Como exemplo da diferença entre média e mediana, suponha que adicionemos mais duas mortes à amostra. Uma morte aos 46 anos e outra aos 81. A probabilidade de chegar aos 80 anos não se altera, mas a expectativa média de vida aos 45 anos diminuiria.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Imagine um elástico infinitamente elástico com 1 km de comprimento quando não esticado. Ele se expande a uma taxa de 1 km por segundo. Agora, imagine uma formiga em uma das extremidades do elástico. No momento em que o elástico começa a se expandir, a formiga rasteja em direção à outra extremidade a uma velocidade, em relação à sua posição atual, de 1 cm por segundo. A formiga chegará à outra extremidade? Se sim, quando?
Sim, irá, após e 100.000 -1 segundos. Veja meu site mathproblems.info , problema 206, para duas soluções.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Você acha que a maior eficiência de combustível compensa o custo adicional de um híbrido? Quantos quilômetros você precisaria percorrer para atingir o ponto de equilíbrio?
Boa pergunta. Para respondê-la, considerei um Toyota Highlander, um veículo que estou pensando em comprar. O preço de tabela do modelo híbrido padrão é de US$ 37.490. Para o mesmo veículo com tração nas quatro rodas, sem sistema híbrido, o preço é de US$ 29.995. Portanto, o motor híbrido adiciona US$ 7.495 ao custo.
O consumo de combustível do híbrido é de 28 mpg (milhas por galão), tanto na cidade quanto na estrada. O consumo do modelo não híbrido é de 17 mpg na cidade e 22 mpg na estrada. Vamos considerar a média de 19,5 mpg.
A fórmula geral para o número de milhas necessárias para atingir o ponto de equilíbrio é h×m h ×m r /(g×(m h -m r )), onde
h = Custo adicional do híbrido.
g = Custo por galão de gasolina.
m r = Quilometragem para veículos não híbridos (o "r" refere-se a um carro convencional).
m h = Autonomia de um híbrido.
A tabela a seguir utiliza essa fórmula para encontrar o ponto de equilíbrio para vários preços de gasolina, de US$ 2 a US$ 5 por galão.
Ponto de equilíbrio híbrido
| Custo da gasolina | Número de milhas |
| $ 2,00 | 240.722 |
| $ 2,25 | 213.975 |
| $ 2,50 | 192.577 |
| $ 2,75 | 175.070 |
| $ 3,00 | 160.481 |
| $ 3,25 | 148.136 |
| $ 3,50 | 137.555 |
| $ 3,75 | 128.385 |
| $ 4,00 | 120.361 | $ 4,25 | 113.281 |
| $ 4,50 | 106.987 |
| $ 4,75 | 101.357 |
| $ 5,00 | 96.289 |
Portanto, ao preço atual de US$ 3,00 por galão aqui em Las Vegas, você precisaria rodar mais de 160.481 milhas com o veículo para que o custo-benefício fosse vantajoso. Isso não leva em consideração outras despesas que podem estar associadas a um híbrido, como o alto custo de substituição das baterias, nem quaisquer pontos positivos percebidos por consumir menos combustível fóssil.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Qual seria a proporção de genes que eu teria em comum com um irmão ou irmã, além de gêmeos idênticos?
1/2.
Se usássemos o jogo de keno como comparação, cada pessoa teria 40 genes, cada um representado por uma bola de keno. No entanto, cada bola teria um número único. Quando duas pessoas, que não são parentes, se acasalam, é como combinar 80 bolas entre as duas em uma caçamba e escolher aleatoriamente 40 genes para a prole desse acasalamento.
Então, quando você foi concebido(a), metade das bolas que estavam no pote foram suas, e a outra metade foi descartada. Quando seu irmão ou irmã foi concebido(a), ele/ela recebeu metade das bolas sorteadas quando você nasceu e metade das bolas que não foram sorteadas. Portanto, vocês são 50% geneticamente idênticos. Isso ocorre pelo mesmo motivo que, se 40 números fossem sorteados no keno, dois sorteios consecutivos teriam, em média, 20 bolas em comum.
Essa questão foi levantada e discutida no fórum do meu site complementar, Wizard of Vegas .
Uma fábrica que produz mesas e cadeiras está equipada com 10 serras, 6 tornos e 18 lixadeiras. Uma cadeira leva 10 minutos para ser serrada, 5 minutos para ser torneada e 5 minutos para ser lixada. Uma mesa leva 5 minutos para ser serrada, 5 minutos para ser torneada e 20 minutos para ser lixada. Uma cadeira é vendida por US$ 10 e uma mesa por US$ 20. Quantas mesas e cadeiras a fábrica deve produzir por hora para obter a maior receita possível, e qual é essa receita?
Vamos considerar c como o número de cadeiras produzidas por hora e t como o número de mesas. A receita por hora será de 10 × c + 20 × t.
As 10 serras resultam em 600 minutos de serragem por hora. Foi-nos informado que uma cadeira leva 10 minutos de serragem e uma mesa, 5. Isso limita a produção horária a:
(1) 10c + 5t <= 600
Os 6 tornos resultam em 360 minutos de torneamento por hora. Foi-nos informado que uma cadeira leva 5 minutos de serragem e uma mesa, 5 minutos. Isso limita a produção horária a:
(2) 5c + 5t <= 360
As 18 lixadeiras resultam em 1080 minutos de lixamento por hora. Foi-nos informado que uma cadeira leva 5 minutos de serragem e uma mesa, 20 minutos. Isso limita a produção horária a:
(3) 5c + 20t <= 1080
O gráfico a seguir mostra as três restrições impostas pelos três conjuntos de máquinas. A fábrica pode produzir qualquer combinação de cadeiras e mesas que esteja sob as três linhas de produção. A questão é: qual dessas três linhas resulta na maior receita?
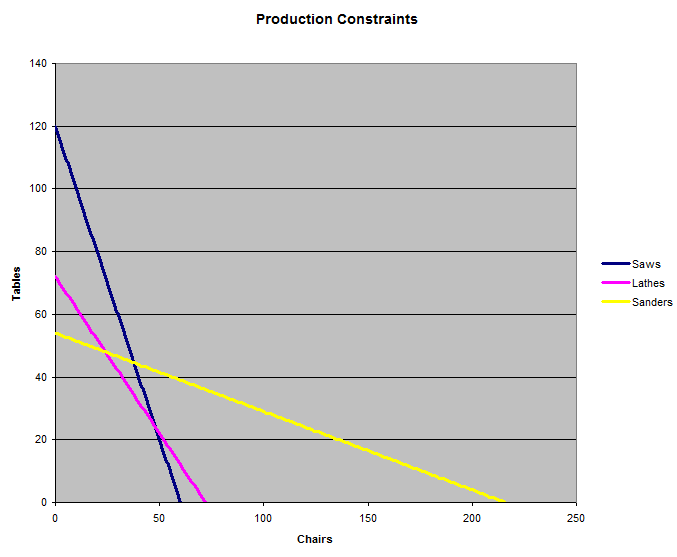
É lógico supor que a resposta seria a intersecção de duas retas, que formariam todas as cadeiras ou todas as mesas. Então, vamos encontrar onde as retas se intersectam. Primeiro, vamos encontrar onde as equações (1) e (2) se intersectam. Podemos substituir a expressão <= por apenas =, para aproveitar ao máximo o potencial das máquinas.
(1) 10c + 5t = 600
(2) 5c + 5t = 360
Subtraia (2) de (1):
5c = 240
c = 48
Substituindo 48 por c na equação (1):
10×48 + 5t = 600
5t = 120
t = 24
Assim, as equações (1) e (2) se encontram em 48 cadeiras e 24 mesas.
Em seguida, vamos encontrar o ponto de encontro das equações (2) e (3):
(2) 5c + 5t = 360
(3) 5c + 20t = 1080
Subtraindo (2) de (3):
15t = 720
t = 48
Colocando isso em (2) ou (3) podemos resolver para c, que é 24.
Assim, as equações (2) e (3) se encontram em 24 cadeiras e 48 mesas.
Não precisamos nos preocupar em encontrar onde as equações (1) e (3) se encontram, porque podemos ver pelo gráfico que onde as linhas da serra e da lixadeira se encontram está fora da restrição do torno.
Também é possível que fabricar apenas cadeiras seja a resposta correta. O gráfico mostra que as serras são a maior limitação para a fabricação exclusiva de cadeiras. A partir da equação (1), se substituirmos o número de mesas por 0, obtemos c = 60.
Outra possibilidade é fazer apenas mesas. O gráfico mostra que as lixadeiras serão a maior limitação. Colocando 0 cadeiras na equação (3), descobrimos que podemos fazer no máximo 54 mesas.
O gráfico a seguir mostra a receita total para cada resposta viável. Lembre-se, a receita é de US$ 10 por cadeira e US$ 20 por mesa.
Receita horária total
| Cadeiras | Tabelas | Receita |
| 0 | 54 | $ 1.080 |
| 24 | 48 | $ 1.200 |
| 48 | 24 | $ 960 |
| 60 | 0 | $ 600 |
O rei tem um barril cheio de vinho.
Na noite de segunda-feira, um criado furta três xícaras do barril e as substitui por três xícaras de água.
Na noite de terça-feira, outro criado furta três copos do barril de vinho, agora diluído, e os substitui por três copos de água.
Na noite de quarta-feira, mais um criado furta três copos do barril de vinho, agora mais diluído, e os substitui por três copos de água.
Na manhã de quinta-feira, o barril contém 50% de vinho e 50% de água.
Qual era a quantidade inicial de vinho no barril?
Aqui está a resposta e a solução (PDF).
Para discutir esse problema, visite meu fórum no Wizard of Vegas .
Se eu tivesse uma tigela com 200 Skittles e 3 deles me matassem, qual a probabilidade de eu morrer se comesse 12 de uma vez? Considere que apenas um Skittle envenenado seria suficiente para me matar.
Para mais informações sobre este assunto, visite meu fórum no Wizard of Vegas .
Um alienígena abduziu dez lógicos e os colocou em uma sala. Ele explica que primeiro os organizará em fila, do mais alto para o mais baixo, com cada pessoa voltada para a direção da pessoa imediatamente mais baixa à sua frente, de modo que cada um possa ver todos os lógicos mais baixos, mas não os mais altos. Em seguida, ele explica que colocará um chapéu preto ou branco em cada um, porém ninguém poderá ver a cor do seu próprio chapéu, apenas a dos chapéus dos lógicos mais baixos. A distribuição de chapéus pretos e brancos pode ser qualquer uma, não necessariamente cinco de cada.
O alienígena então explica que perguntará a cada lógico, começando pelo mais alto e seguindo até o final da fila, a cor do seu chapéu. Os lógicos poderão ouvir a resposta daqueles que agiram antes deles. Além das respostas preto/branco, eles não poderão se comunicar de nenhuma outra forma depois que o jogo começar. Se mais de um lógico errar, todos serão devorados. Se pelo menos nove respostas estiverem corretas, eles retornarão em segurança para a Terra. O alienígena então lhes dá um tempo para elaborar uma estratégia. Qual deve ser a estratégia deles?
Segue uma possível estratégia. O primeiro lógico a agir deve dizer "preto" se vir um número par de chapéus pretos e "branco" se vir um número ímpar de chapéus nos outros nove lógicos. Ele terá 50% de chance de acertar a cor do seu próprio chapéu, portanto, ele é o único que pode errar. Seja qual for a resposta dele, defina-a como a "cor da vez".
Em seguida, o segundo lógico a agir contará os chapéus pretos nos oito lógicos menores e os associará a uma cor usando o mesmo método de paridade do primeiro lógico. Se a contagem coincidir com a cor indicada pelo primeiro lógico, então ele deve ter um chapéu branco e deve dizer "branco". Se a contagem for diferente, ele deve ter um chapéu preto e deve dizer "preto". Se ele disser "branco", a cor em questão permanecerá a mesma. Se ele disser "preto", a cor em questão mudará para a cor oposta.
Em seguida, o terceiro lógico a agir fará exatamente o mesmo que o segundo, mas contando os chapéus pretos dos sete lógicos mais baixos. Da mesma forma, se ele concordar com a cor em circulação, dirá "branco" e a cor em circulação permanecerá a mesma. Se ele discordar da cor em circulação, dirá "preto" e a cor em circulação será invertida.
Cada um dos outros lógicos fará exatamente a mesma coisa.
É claro que eles poderiam facilmente associar o preto a um total ímpar e o branco a um total par. O importante é que todos concordem com qual cor representa qual paridade (ímpar/par). Seguindo qualquer uma das estratégias, os lógicos do segundo ao décimo a agir estarão corretos e o primeiro terá 50% de chance de acertar, então todos sobreviverão. Essa estratégia funcionará para qualquer número de lógicos.
Axel e Bob têm cada um seu próprio baralho de 52 cartas. Ambos embaralham os baralhos aleatoriamente. Em seguida, viram uma carta de cada vez, simultaneamente, de cada baralho. Qual é a probabilidade de que eles virem a mesma carta ao mesmo tempo pelo menos uma vez?
Seria fácil estimar a resposta como 1-(51/52) 52 = 0,63568648. No entanto, estimativas são intelectualmente insatisfatórias. Então, vamos encontrar uma solução exata!
Passo 1: Para começar, considere o número de maneiras pelas quais o segundo baralho pode ser ordenado onde a primeira carta é o número 1. A resposta é o número de maneiras de ordenar as outras 51 cartas, que é 51! = 1551118753287382280224243016469303211063259720016986112000000000000.
Qualquer carta pode combinar com o primeiro baralho, então devemos fazer isso para todas as 52 cartas. Isso nos dá 52 * 51! = 52! combinações onde pelo menos uma carta combina.
Passo 2: No entanto, o passo 1 conta duas vezes cada situação em que duas cartas combinam. Por exemplo, se as duas primeiras cartas fossem 1 e 2, teríamos contado as 50! maneiras de organizar as outras cartas duas vezes, uma vez com 1 como a primeira carta e uma segunda vez com 2 como a segunda carta. O número de maneiras de escolher 2 cartas dentre 52 é combin(52,2) = 1326. Para cada combinação de duas cartas, existem 50! = 30414093201713378043612608166064768844377641568960512000000000000 maneiras de ordenar as outras cartas. Assim, para o passo 2, precisamos subtrair combin(52,2)*50! = (52*51/2!)*50! = 52!/2! combinações.
Passo 3: Em seguida, considere a situação em que as três primeiras cartas do baralho aleatório são 1, 2 e 3, nessa ordem. Existem 49! maneiras de ordenar as outras 49 cartas. Teríamos contado essas combinações três vezes na etapa inicial de contagem de pelo menos uma carta correspondente. Depois, teríamos subtraído todas as combinações (3,2) = 3 maneiras de escolher 2 dessas três cartas na segunda etapa. Portanto, essa situação teria sido contada 3 - 3 = 0 vezes, então precisamos adicioná-las novamente. Existem combinações (52,3) de situações em que se escolhe pelo menos 3 cartas correspondentes. Assim, precisamos adicionar de volta combinações (52,3) * 49! = 52 * 51 * 50 * 49! / 3! = 52! / 3! combinações.
Passo 4: Em seguida, considere a situação em que as quatro primeiras cartas do baralho aleatório são 1, 2, 3 e 4, nessa ordem. Existem 48! maneiras de ordenar as outras 48 cartas. Teríamos contado cada uma delas quatro vezes na etapa inicial de contagem, buscando pelo menos uma carta correspondente. Depois, teríamos subtraído todas as combinações (4,2) = 6 maneiras de escolher duas dessas quatro cartas na etapa 2. Em seguida, teríamos adicionado todas as combinações (4,3) = 4 maneiras de escolher 3 dessas quatro cartas. Portanto, temos 4 - 6 + 4 = 2 maneiras de cada situação ser contada. Assim, precisamos subtrair uma dessas maneiras, para que cada situação seja contada apenas uma vez. Existem combinações (52,4) * 48! = 52 * 51 * 50 * 49 * 48! / 4! = 52! / 4! situações que precisam ser adicionadas novamente.
Continuaremos fazendo isso, alternando adições e subtrações para corrigir a contagem dupla.
No final, o número de situações em que pelo menos uma carta no baralho aleatório corresponde ao baralho ordenado = combin(52,1)*51! - combin(52,2)*50! + combin(52,3)*49! - combin(52,4)*48! ... - combin(52,52)*1! = 52!/1! - 52!/2! + 52!/3! - 52!/4! ... - 52!/52! = x = 333239808909468890675694068318655265019682314241643033726180828783.
Existem 52! = y = 527177615496365219422618541545122659969212453861982208000000000000 maneiras totais de ordenar 52 cartas.
Portanto, a resposta é x/y = 0,6321205588285576784044762298
A probabilidade de não haver correspondências é 1-(x/y) = 0,3678794411714423215955237702.
Se esse número lhe parece familiar, é porque deveria. 1/e = 0,3678794411714423215955237702.
Portanto, a resposta pode ser estimada com bastante precisão como 1-(1/e).
Agradecimentos
Os cálculos matemáticos foram realizados em Pari/GP
Este problema foi levantado e discutido no meu fórum no Wizard of Vegas .
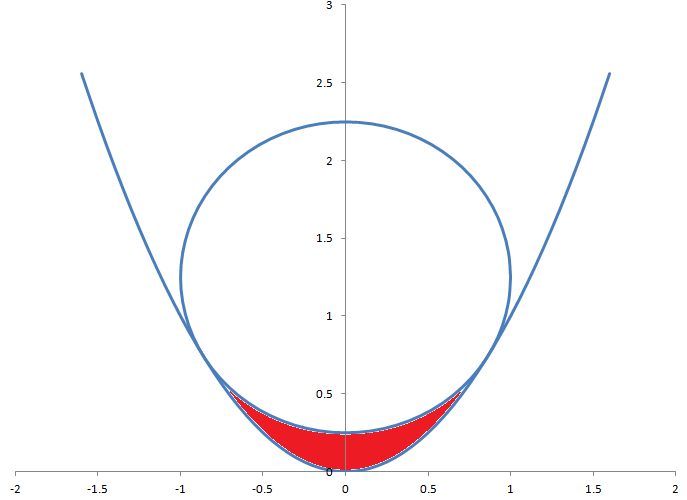
Um círculo de raio 1 é tangente a uma parábola de equação y = x² . Qual é a área da região em vermelho entre o círculo e a parábola?
Clique no botão abaixo para ver a resposta.
Aqui está minha solução . (PDF)
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Recebi essa informação de Presh Talwalker, da Mind Your Decisions .
Uma crupiê está trabalhando em uma nova variante do Three Card Poker. Ela pega todas as cartas com figuras de um baralho padrão e as embaralha completamente. Em seguida, distribui 3 cartas para o Jogador 1, 3 cartas para o Jogador 2, 3 cartas para o Jogador 3 e as 3 cartas finais para o Jogador 4. Qual é a probabilidade de que todas as quatro mãos contenham uma sequência (JQK de qualquer naipe)?

A probabilidade da primeira mão ser AKQ é 1*(8/11)*(4/10) = 29,09%.
A probabilidade de a segunda mão ser AKQ, dado que a primeira já é, é igual a 1*(6/8)*(3/7) = 32,14%.
A probabilidade de a terceira mão ser AKQ, dado que a primeira e a segunda já são, é igual a 1*(4/5)*(2/4) = 40,00%
As cartas restantes devem ser AKQ, visto que as três primeiras mãos são. Portanto, a probabilidade é o produto das três probabilidades acima, que é 216/5775 = aproximadamente 0,037402597.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Qual é a área e o perímetro médios de um retângulo inscrito aleatoriamente em um círculo de raio 1?
Boa pergunta. Aqui estão minhas respostas:
Aqui está minha solução para ambos os problemas (PDF).
Encontre um número de dez dígitos tal que:
- O primeiro dígito do número representa a quantidade de zeros (ou seja, a quantidade de zeros) no número inteiro.
- O segundo dígito do número representa a quantidade de 1s no número inteiro.
- O terceiro dígito do número representa a quantidade de 2s presentes no número inteiro.
- O quarto dígito do número representa a quantidade de 3s presentes no número inteiro.
- O quinto dígito do número representa a quantidade de 4s presentes no número inteiro.
- O sexto dígito do número representa a quantidade de 5s presentes no número inteiro.
- O sétimo dígito do número representa a quantidade de 6s presentes no número inteiro.
- O oitavo dígito do número representa a quantidade de 7s presentes no número inteiro.
- O nono dígito do número representa a quantidade de 8s presentes no número inteiro.
- O décimo dígito do número representa a quantidade de 9s presentes no número inteiro.
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Três pontos estão distribuídos aleatoriamente e uniformemente ao longo de um círculo de raio 1. Qual é a distância mínima esperada entre os três pontos, onde as distâncias são medidas ao longo da circunferência?
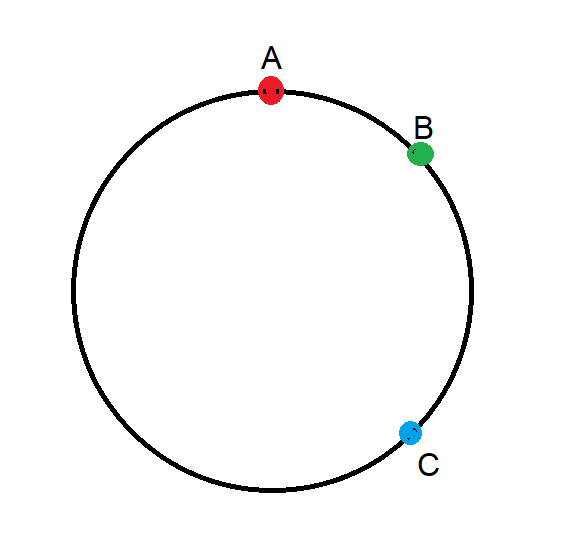
Aqui está minha solução (PDF).
Essa pergunta é feita e discutida no meu fórum, Wizard of Vegas .
Alice e Bill levam 3 horas para pintar uma casa.
Alice e Cindy levam 4 horas para pintar uma casa.
Bill e Cindy levam 5 horas para pintar uma casa.
Quanto tempo leva se todos eles pintarem?
Aqui está minha solução (PDF).


